高速铁路同相供电原理

1．功率守恒原则

坐标变换必须遵守功率守恒定律，包括功率守恒定律、功率守恒伴随式、电压电流功率守恒对偶式。

1）功率守恒定律

功率守恒是基本规律，不管什么类型的变压器，其输入的功率恒等于变压器内部损失的功率与变压器输出功率之和。如果忽略变压器的内部损耗，变压器的输入功率必须等于变压器的输出功率；而变压器输出的功率又必须等于负载吸收的功率。

为不失一般性，假定牵引变压器一次侧有N相，二次侧有k相，原次边及负荷端口的电压、电流向量如图1.4所示，其中，

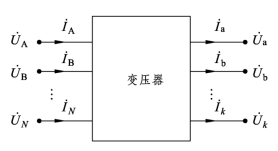
图1.4　变压器多端口网络

——N行1列变压器原边电压向量矩阵，；

——N行1列原边电流向量矩阵，；

——的共轭矩阵；

——k行1列变压器次边电压向量矩阵，；

——k行1列次边电流向量矩阵，；

——的共轭；

——分别为负载端口的电压、电流向量，m表示第m个端口，负载可以接于相与相之间，也可以接于相上；在牵引变压所中牵引负荷都是接于端口上。

为表述方便，定义两个集合Y={A B…N}，X={ab…k }，两个集合的元素由相序符号组成。

功率守恒式可写为分别为变压器原边输入功率、次边输出功率和负载所消耗的功率，当忽略变压器各种损耗时，三者必然恒等，所以称式（1.33）为功率守恒式。

3）电压、电流对偶式

对于一个确定的变压器，原次边电压以及原次边电流之间的关系是确定的，总是可以写为

式中，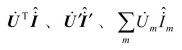

(https://www.xing528.com)

式中，Q为N行k列的电压变换矩阵；M为k行N列电流变换矩阵。且对于任何变压器M和Q都恒为实数矩阵。将式（1.34）代入式（1.33）可得

由于Q和M都为实数矩阵，所以

式（1.36）说明对于任何一种变压器，电流变换矩阵恒等于电压变换矩阵的转置。式（1.34）可改写为

式（1.37）电流变换式与电压变换式有对偶关系，只要功率守恒，变压器原次边电压、电流就有如式（1.37）的关系，所以称其为电压电流对偶式。

3）功率守恒伴随式

对于变压器还有一个与功率守恒相似的恒等式，可用下式表示

式（1.38）为什么也能够成立呢？我们利用功率守恒式和电压电流对偶式给出证明。根据式（1.37）容易得

所以式（1.38）左半部分等式成立。现证明式（1.38）右半部分等式也成立。假设负载接于变压器次边第i相与第j相之间，则有

式中，为负荷电流。则

式中，为负载端口电压，也即第i相电压与第j相电压之差值。如果有m个负载接于不同端口时，可应用叠加原理，同样可证明式（1.38）右半部分成立。

值得说明的是，当负载并非接于相与相之间而是接于任意一相上或几个相上时，应用相同方法可证明式（1.38）依然成立。

以上证明利用了变压器的功率守恒定律和电压电流对偶式，二者对于所有变压器都是成立的，所以当忽略变压器内部损耗时，式（1.38）与功率守恒关系式一样也是恒等式，我们将式（1.38）称为功率守恒伴随式。

2．磁势平衡原则

前文已述及，不管怎样变换，变换前后电机中的旋转磁势不应该发生改变；变压器铁芯上的各相绕组磁势满足磁势平衡，也即，总合成磁势为零，此时变压器原边各相合成磁势等于次边各相合成磁势。