旋转矢量的定义及其关系与特点

1．旋转矢量的概念

设一个复数的指数形式为

式中，Im为复数的模；φ 为初相角，也就是相对于参考轴实轴的夹角。将复数画在复平面上就是一个长度为Im、初相角为φ 的静止不动的矢量。在电路中一般称它为电流向量。如果式（1.1）右边乘以因子ejωt，用表示以区别静止的电流向量，即

这时矢量将随着时间的增长围绕着原点逆时针方向旋转，所以称其为旋转矢量，如图1.1所示，旋转的角速度为ω，初相角φ 为t=0时矢量与参考轴的夹角。

2．旋转矢量与瞬时值之间的关系

图1.2（a）为旋转矢量在两相坐标轴上的投影，其中α、β代表两相坐标轴，两坐标轴相差90°；φα为α 坐标轴与参考轴OO的夹角。根据矢量合成与分解的平行四边形法则，可得

图1.1　旋转矢量(www.xing528.com)

式中　iα、iβ——分别为在坐标轴α、β 上的投影值。由于随时间旋转，所以iα、iβ随时间不断变化，是时间的函数，称为两相坐标系下的瞬时值。而坐标轴与参考轴的夹角恒定不变，分别为-αφ，，所以。

式中，iA、iB、iC分别为在坐标轴A、B、C上的投影值，同样由于随时间旋转，所以iA、

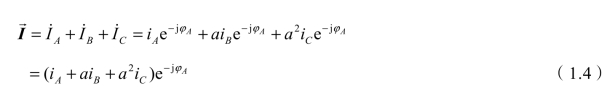
图1.2（b）为旋转矢量与其在三相坐标轴上的投影，A、B、C为三相坐标轴，坐标轴彼此相差120°，φA为A坐标轴与参考轴OO的夹角。根据矢量合成与分解的平行四边形法则，同样可得iB、iC是随时间不断变化的量值，称为三相坐标系下的瞬时值；a为单位矢量因子或称为旋转因子，对于三相坐标系。根据图1.2（b）坐标关系有，。

图1.2　旋转矢量与瞬时值之间的关系

特别当A相坐标轴和α 坐标轴分别与参考轴OO重合时，则