车辆结构有限元分析：应变疲劳基础

1.应变疲劳性能

在整个应变疲劳分析流程中，第一步是定义ε-N曲线，ANSYS Workbench中ε-N曲线的定义是通过应变寿命曲线的参数定义的，如图9-78所示。

（1）应变疲劳性能曲线的描述

应变疲劳性能定义的是应变与寿命之间的关系，用ε-N曲线来描述。因为应变疲劳研究的是载荷大（超过屈服应力）、寿命短（一般小于10⁶）的情况，故试验时加载频率通常较低（0.1～1Hz）。

按照标准试验方法，在R=-1的对称循环下，进行给定应变幅下的对称恒幅循环疲劳试验，可得到图9-79所示的一般规律。图中，载荷用应变幅ε_a表示，寿命用载荷反向次数2N表示。注意到一个载荷循环有两次反向，N即为循环次数。应变幅ε_a越小，寿命N就越长；低于某一载荷水平，寿命可以趋于无穷大。

由试验记录可知应变幅ε_a、应力幅σ_a和破坏时的循环次数2N_f。将总应变幅ε_a写成弹性应变幅ε_ea和塑性应变幅ε_pa两部分，有

ε_ea=σ_a/Eε_pa=ε_a-ε_ea

分别画出lgε_ea-lg（2N_f）、lgε_pa-lg（2N_f）的关系，如图9-79中直线所示，二者呈对数线性关系。由此，可分别有

式（9-21）反映了弹性应变幅ε_ea与寿命2N间的关系，σ_f′称为疲劳强度系数，具有应力量纲；E为弹性模量，b为疲劳强度指数。式（9-22）反映了塑性应变幅ε_pa与寿命2N间的关系，ε_f′称为疲劳延性系数，与应变一样，无量纲；c为疲劳延性指数。b、c分别为图中两直线的斜率。对于大多数金属材料，疲劳强度指数b一般为-0.06～0.14，估计时可取0.1。疲劳延性指数c一般为-0.7～0.5，常取-0.6作为其典型值。综合式（9-21）和式（9-22）ε-N曲线可写为

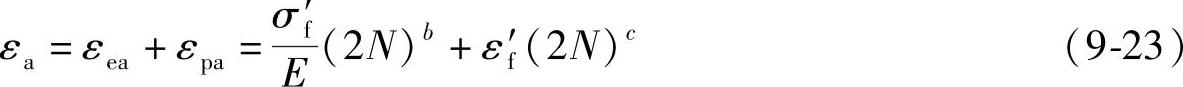
图9-78 ANSYS Workbench中ε-N曲线的定义

图9-79 典型的应变疲劳特性曲线

如图9-79所示，在长寿命阶段，以弹性应变幅ε_ea为主，塑性应变幅ε_pa的影响可忽略，ε_a≈ε_pa，所以或写为ε^m_ea1N=C₁

在短寿命阶段，以塑性应变幅ε_pa为主，弹性应变幅ε_ea影响可以忽略，ε_a≈ε_pa，且有

ε_pa=ε_f′（2N）c或写为

这就是著名的Manson-Coffin低周应变疲劳公式（1963年）。当ε_ea=ε_pa时，有

由此可求得

若寿命大于2N_t，以弹性应变为主，是应力疲劳；寿命小于2N_t，以塑性应变为主，是低周应变疲劳（图9-79）。因此2N_t被称为临界寿命

式（9-23）中，ε_a可以通过由σ_a-ε_a关系求取。不同应变恒幅对称循环控制下的疲劳试验，可得到一族稳态滞后环。将这些稳态环置于同一坐标内，如图9-80所示。各稳态滞后环顶点的连线反映了不同应变幅ε_a循环下的应力幅σ_a响应，由此所给出的σ_a-ε_a关系，称为循环σ_a-ε_a曲线。

图9-80 循环应力-应变曲线

值得注意的是，与单调σ-ε曲线不同，循环载荷作用下的σ_a-ε_a曲线，并不反映加载路径，反映加载路径的是滞后环。

循环σ_a-ε_a曲线，可以按照式（9-24）进行数学描述，即

式中，K′为循环强度系数，具有应力量纲（MPa）；n′为循环应变硬化指数，是无量纲量。对于大多数金属材料，循环应变硬化指数n′之值一般在0.1～0.2之间。

将应变幅ε_a写为弹性应变幅ε_ea与塑性应变幅ε_pa两部分，分别表示它们与应力幅的关系，有

σ_a=Eε_eaσ_a=K′（ε_pa）n′

由此，已知应变幅ε_a，则可知ε_ea=σ_a/E，与其相应的塑性应变幅则为ε_pa=ε_a-ε_ea。

滞后环曲线（Δσ-Δε曲线）：

如前所述，循环应力-应变曲线给出的是在不同应变幅ε_a控制下，循环稳定状态时的应力幅σ_a，它不反映实际的σ-ε加载路径。反映加载路径的是滞后环曲线。

对于拉压性能对称的材料，其滞后环曲线的上升与下降两个半支是关于原点对称的，如图9-81所示，故只需考虑半支即可。

以滞后环曲线下顶点O′为坐标原点，考虑滞后环曲线的上升半支。注意此时的坐标轴分别为应力变程Δσ和应变变程Δε。

图9-81 滞后环曲线

在试验观察的基础上，假设滞后环曲线与循环应力-应变曲线几何相似，即在σ_a-ε_a坐标系中的σ_a、ε_a分别是Δσ-Δε坐标系中的Δσ/2和Δε/2，由二者的相似性，并仿照式（9-24）可写出滞后环曲线为

或

上述假设称为Massing假设。满足这一假设的材料，称为Massing材料。式（9-25）是反映加载路径的滞后环曲线。

同样，若用应变表示应力，则有

Δσ=EΔε_e和Δσ=2K′（Δε_p/2）^n′

（2）应变疲劳性能曲线的估算

在应变控制下，一般金属材料的ε-N曲线有图9-82所示的特征。即当应变幅ε_a=0.01时，许多材料都有大致相同的寿命。在高应变范围内，寿命的增加主要取决于材料的延性；而在低应变、长寿命阶段，强度高的材料，寿命长一些。

图9-82 不同金属的应变-寿命曲线

1965年，Manson在研究了钢、钛铝合金材料的大量试验结果基础上，提出了一个由材料单调拉伸性能估计ε-N曲线的经验公式：

式中，S_u为材料的极限强度；ε_f为断裂真应变。二者均可由单调拉伸试验得到。

2.平均应力的修正

式（9-23）和式（9-26）给出的关于ε-N曲线的估计，仅可用于恒幅对称应变循环性能。考虑平均应力或平均应变的影响会使式（9-26）变得非常复杂，在ANSYS Workbench中，有两种平均应力的修正方法可供选择，包括Morrow法和SWT法，当然也可以选择不修正None。

（1）Morrow法

Morrow法是美国汽车工程师协会（SAE）的疲劳设计手册中的推荐方法，如式（9-27）所示。

式中，σ_m为平均应力。在对称循环时，σ_m=0。注意到b<0、c<0，当寿命N相同时，平均应力越大，可承受的应变幅ε_a越小；或应变幅不变，平均应力越大，则寿命N越短。可见，拉伸平均应力是有害的，压缩平均应力则可提高疲劳寿命。

Morrow法在美国应用比较广泛，这是由于在以压缩应力为主的应力状态，用这种方法计算损伤要比用Smith-Watson-Topper方法简便。

（2）SWT方法

SWT方法，又被称为Smith-Watson-Topper方法，是Smith等人为了考虑平均应力的影响，对试验结果进行了分析，提出用σ_maxΔε来计算损伤，并推导出了以下损伤计算公式：

Smith-Watson-Topper公式包含了应力和应变幅值、平均应力对疲劳损伤的影响，已被证明与多种工况的物理试验结果相一致。

3.应变疲劳寿命的估算方法

对于应变疲劳寿命估算，需要把应变（包括弹性应变和塑性应变）参数作为输入，但是当结构总体上响应在弹性范围内的情况下，用有限元分析方法确定这一应变是非常奢侈（主要表现在需要占用计算机的资源非常大）和浪费的，这时可以采用线性方法或Neuber方法将应力集中位置的名义应力/应变转化成为局部应力/应变。

（1）线性方法

假定应变集中系数K_ε等于弹性应力集中系数K_t，即

K_t=ε/e=K_ε （9-28）这称为应变集中的不变性假设，可用于平面应变情况。

已知名义应力S，由应力-应变关系可求名义应变e；或已知名义应变e，由应力-应变关系求出名义应力S；然后利用线性理论，即可确定缺口局部应变为

ε=K_te

（2）Neuber方法

Neuber方程给出的应力和应变关系如式（9-29）所示。

σε=K²_teS （9-29）(www.xing528.com)

式（9-29）称为Neuber双曲线。由此补充方程与应力-应变关系式一起，即可联立求解缺口局部应力σ和局部应变ε。图9-83中，Neuber双曲线与材料σ-ε曲线的交点D，即为Neuber理论的解答值。

例如，已知材料弹性模量E=60 GPa，单调强度系数K=2000MPa，单调硬化指数n=0.125。若缺口名义应力S=600MPa，弹性应力集中系数K_t=3，求缺口局部应力、应变。

图9-83 缺口局部应力-应变

已知S=600MPa，材料应力-应变曲线为

e=S/60000+（S/2000）8

求得名义应变为

e=0.01+（0.3）8≈0.01

1）线性理论

ε=K_te=3×0.01=0.03

由材料应力-应变曲线

ε=0.03=σ/60000+（σ/2000）8

可解出

σ=1138MPa

2）Neuber理论

由Neuber双曲线方程可得

σε=K²_teS=9×0.01×600=54

由材料应力-应变曲线可得

ε=0.03=σ/60000+（σ/2000）8

联立后得到

σ/60000+（σ/2000）8=54/σ

可解出

σ=1245MPa

且有

ε=54/σ=0.043

由此可见，用Neuber理论估计的σ、ε大于线性理论，是偏于保守的。故工程中常用Neuber理论进行缺口应力-应变估计，这一方法也是ANSYS Workbench采用的方法。

下面讨论利用ε-N曲线进行疲劳寿命估算的方法。假定已知应变或应力时间历程，首先要进行循环响应的计算，寻找出应力-应变响应的稳定循环，并由稳态环确定循环应变幅ε_a和平均应力σ_m，然后利用式（9-27）估算寿命。

图9-84 三种应变时间历程

作为特例，构件承受的是恒幅对称循环（σ_m=0），则可利用式（9-23），直接由已知的应变幅ε_a估算疲劳寿命。

例如，已知某材料E=210GPa，n′=0.2，K′=1220MPa，σ_f′=930MPa，b=-0.095，c=-0.47，ε_f′=0.26，试估计在图9-84所示三种应变下的寿命。

第一个载荷谱块为恒幅值应变对称循环，且ε_a=0.005；σ_m=0。

直接由ε-N曲线式（9-27）估算寿命，有

求得2N=11716，N=5858次循环。

第二个载荷谱块为非恒幅应变循环，疲劳寿命按如下步骤进行计算：

1）计算σ-ε响应如下：

0—1　ε₁=0.02=σ₁/E+（σ₁/K′）1/n′可得σ₁=542MPa

1—2　Δε_1-2=0.025=Δσ_1-2/E+2（Δσ_1-2/2K′）1/n′

求得Δσ_1-2=972MPa

有ε₂=ε₁-Δε_1-2=-0.005

σ₂=σ₁-Δσ_1-2=-430MPa

2—3 Δε_2-3=0.01， 因此有Δσ2_-3=772MPa

有ε₃=0.005　σ₃=342MPa

3—4注意到2—3—4形成封闭环，有ε₄=ε₂=-0.005，σ₄=σ₂=-430MPa。

2）画σ-ε响应曲线，如图9-85所示，图中稳态环为ε_a=（ε₃-ε₄）/2=0.005，σ₄=σ₂=-430MPa，σ_m=（σ₄+σ₃）/2=-44MPa

3）估算寿命

代入数值后解得2N=12340，所以，N=6170次循环。

可见，拉伸高载后引入了残余压应力（σ_m<0），疲劳寿命延长，是有利的。

对于第三个载荷谱块，同样可以按照如下步骤进行计算：

1）循环响应计算：

0—1 ε₁=0.02=σ₁/E+（σ₁/K′）1/n′可得：σ₁=542MPa

注意到拉压对称性且此处是压缩，故ε₁=-0.02时，σ₁=-542MPa

由滞后环曲线计算后续响应得

1—2 ε₂=0.005，σ₂=430MPa

2—3 ε₃=-0.005，σ₃=-342MPa

图9-85 载荷谱块2作用下的 应力-应变循环

2）画σ-ε响应曲线，如图9-86所示，求得

ε_a=0.005

σ_m=（σ₄+σ₃）/2=-44MPa

3）由式（9-27）求寿命得

2N=11130，N=5565

因此有5565次循环。

可见，压缩高载后引入了残余拉应力（σ_m﹥0），使疲劳寿命缩短，是有害的。

4.载荷类型

同应力疲劳分析。

图9-86 载荷谱块3作用下的应力-应变循环

5.疲劳强度系数K_f

K_f是疲劳强度系数，又称为疲劳强度缩减系数（Fatigue Strength Reduction Factor）。在进行应变疲劳分析过程中，通过这一系数对ε-N曲线进行调整。这一系数用于考虑结构实际服役环境比实验室条件更为严酷。通常疲劳强度系数用于反映表面加工状态等因素对疲劳强度的影响，这一参数的选择可以参考相关手册。

6.应力分量的选取

同应力疲劳分析。