车辆结构材料疲劳分析成果

Q235钢材断裂强度为439MPa，S-N曲线的数据表达式为lgN_p=a_p+b_plgs，99.9%概率下的a_p=19.8662，b_p=-6.2982。交变载荷F=94200N（图9-25）。

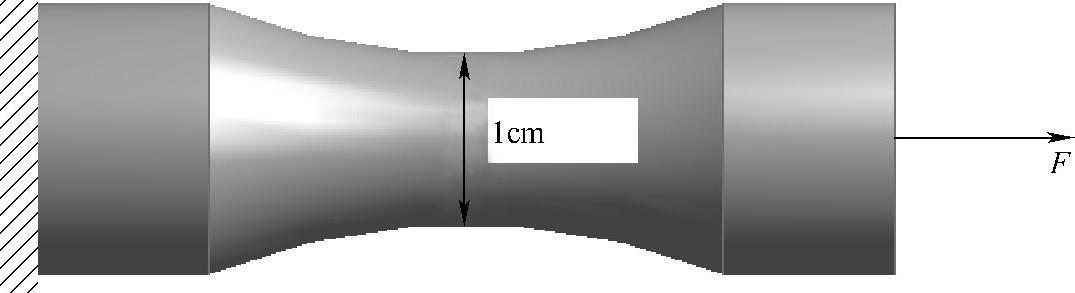
图9-25 材料疲劳特性试件

1.建立疲劳分析项目

首先启动ANSYS Workbench，建立一个静力学分析流程的疲劳分析项目（图9-26），另存项目名称为shaft-fatigue.wbpj。

图9-26 建立疲劳分析项目

2.导入几何模型

用鼠标左键单击选择A3—Geometry，单击鼠标右键，在弹出菜单中选择Import Geometry﹥Browse，在弹出对话框选择随书光盘中的文件Geom.agdb，如图9-27所示。

3.添加材料特性

双击B2—Engineering Data，打开材料特性数据库。选择Structural Steel，在材料特性窗口单击Alternating Stress Mean Stress，如图9-28所示。

图9-27 导入几何模型

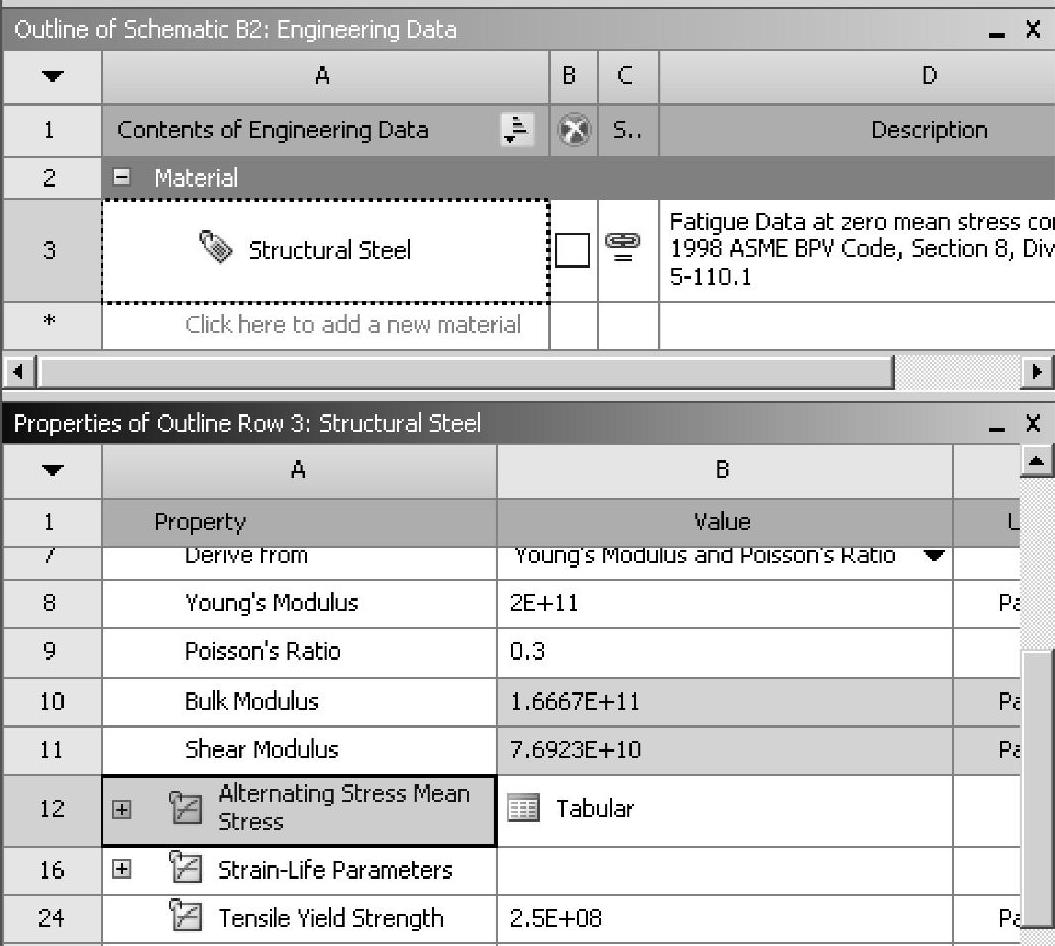
图9-28 查看材料的疲劳特性

这时出现结构钢Structural Steel的疲劳特性，即S-N曲线和对应的数据表，如图9-29所示。

双击B2—Engineering Data，单击鼠标左键选择Structural Steel，单击鼠标右键，在弹出的菜单中选择duplicate，如图9-30所示。生成新的材料Structural Steel2。

选择Structural Steel2，将其更名为Q235，如图9-31所示。

图9-29 结构钢Structural Steel的疲劳特性

图9-30 复制材料Structural Steel

单击鼠标左键选择Q235属性中（图9-31）Alternating Stress Mean Stress右侧的Tabular，接下来需要修改图9-32所示的材料的疲劳特性数据。

对于大多数工程问题，和本节给出的算例相同，一般给出材料的S-N曲线，需要在ANSYS Workbench中对其进行定义。将本题给出的Q235钢材的S-N曲线方程变形后可以得到

a_p=19.8662，b_p=-6.2982

根据上式可以计算不同疲劳寿命下对应的疲劳强度，这一计算可以采用Excel软件方便地实现。图9-32表格中的数据可以直接复制到Excel软件中的电子表格中，输入公式=10^（（LOG（A1）-19.8662）/（-6.2982））*1000000，计算出不同疲劳寿命下对应的疲劳强度，如图9-33所示。

可以将图9-33所示的B栏的疲劳特性数据直接复制，覆盖图9-32中的Alternating Stress一栏，如图9-34所示。

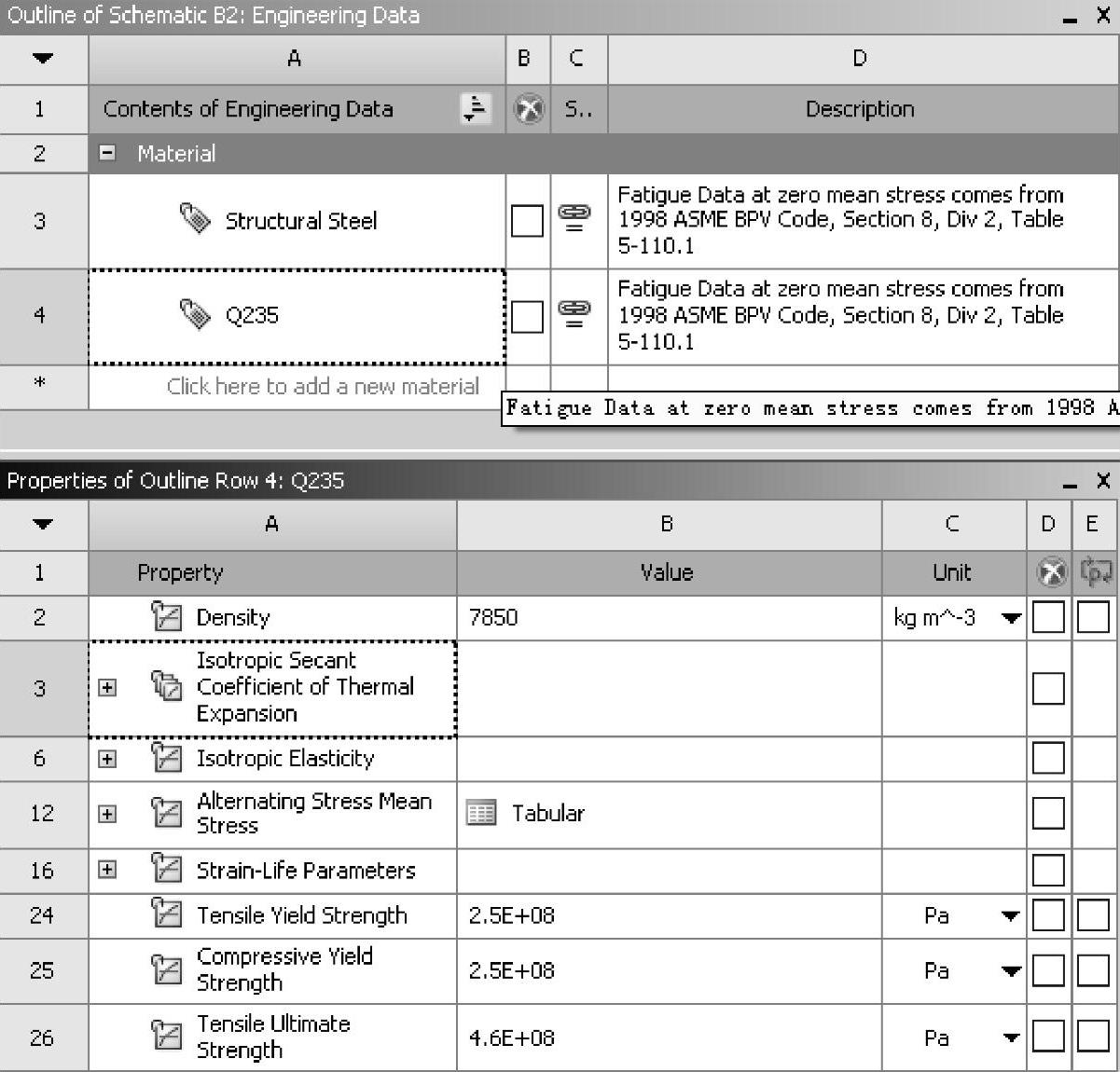
图9-31 定义材料Q235

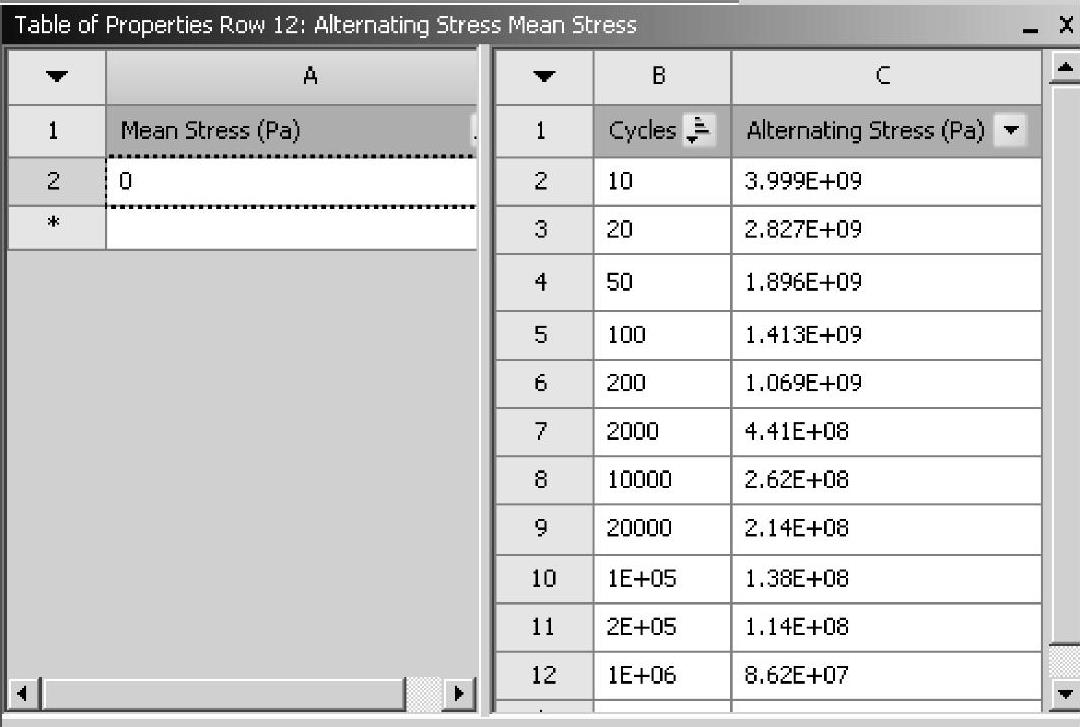
图9-32 待修改的材料的疲劳特性数据

单击工具栏上的按钮，系统返回到ANSYS Workbench主界面，如图9-26所示。

双击A4—Model，启动ANSYS Workbench Mechanical。用鼠标左键单击选择模型树中的Geometry﹥Solid，查看细节窗口Material﹥Assignment对应的材料为Q235，如图9-35所示。

图9-33 不同疲劳寿命对应的疲劳强度计算

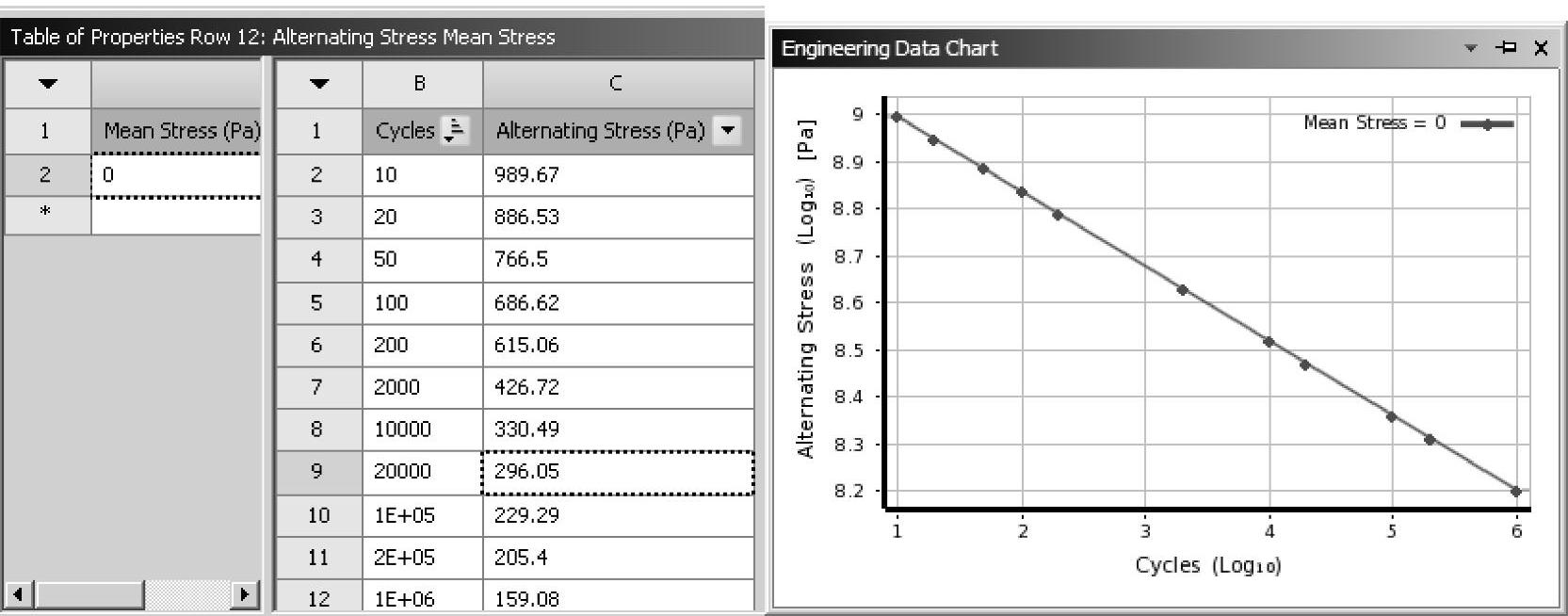
图9-34 Q235的疲劳特性

4.建立有限元模型

（1）定义网格尺寸

双击A4—Model，启动ANSYS Workbench Mechanical。用鼠标右键单击模型树中的Mesh，在弹出的菜单中选择Insert﹥Sizing，单击工具栏上的拾取工具按钮，选择几何图形区的直线，然后单击详细栏中的Apply按钮，在细节窗口按照图9-36所示进行设置。将直线分为10份，Type设置为Number of Divisions，Number of Divisions设置为10。

（2）生成网格

为了提高计算精度，采用六面体进行网格划分。用鼠标右键单击模型树中的Mesh，在弹出的菜单中选择Insert﹥Method，单击鼠标左键选择轴，在细节栏单击Apply按钮，将Method设置为Sweep，如图9-37所示。在工具栏单击按钮，单击模型树中的Mesh，生成的网格如图9-37所示。(www.xing528.com)

图9-35 将材料特性赋值给几何模型

图9-36 定义网格尺寸

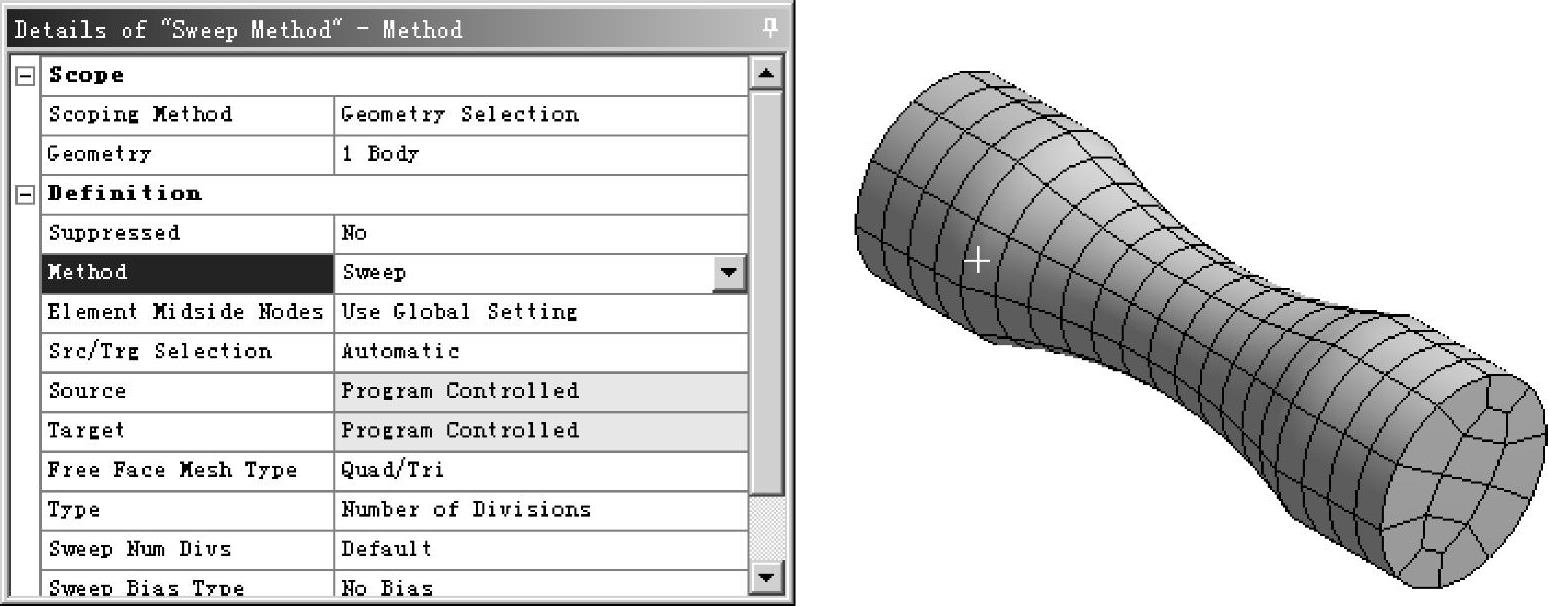
图9-37 定义网格划分方式与网格生成

（3）施加载荷/约束

用鼠标右键单击模型树中的Modal（A5），在弹出的菜单中选择Insert﹥Fixed Support，单击工具栏上的拾取工具按钮，选择轴左侧端面，单击细节窗口中的Apply按钮，如图9-38所示。

图9-38 定义约束

用鼠标右键单击模型树中的Modal（A5），在弹出的菜单中选择Insert﹥Force，单击工具栏上的拾取工具按钮，选择轴；在细节窗口设置轴向的力为94200N，如图9-39所示。

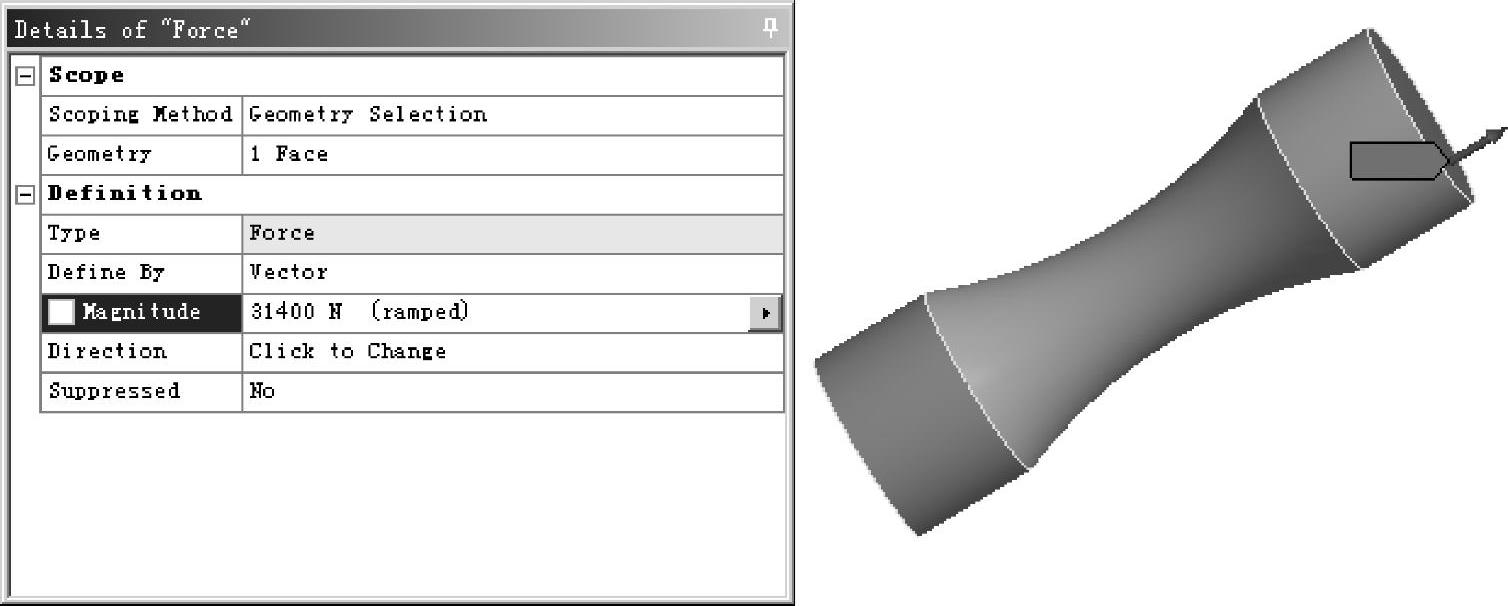
图9-39 定义载荷

（4）定义分析结果

用鼠标右键单击模型树中的Solution（A6），在弹出的菜单中选择Insert﹥Stress﹥Normal，默认应力方向为X方向，如图9-40所示。

用鼠标右键单击模型树中的Solution（A6），在弹出的菜单中选择Insert﹥Fatigue﹥Fatigue Tool；用鼠标右键单击模型树中的Fatigue Tool，在弹出的菜单中选择Insert﹥Life。定义完毕后，模型树如图9-41所示。

5.求解

设置疲劳分析方法，应力计算参数选择为X方向的正应力，计算方法为应力疲劳寿命分析方法，如图9-42所示。

用鼠标右键单击模型树中的Modal（A5），在弹出的菜单中选择Solve，进行求解。

6.查看分析结果

用鼠标左键单击模型树中的Normal Stress，X方向的正应力结果如图9-43所示。

图9-40 定义应力方向

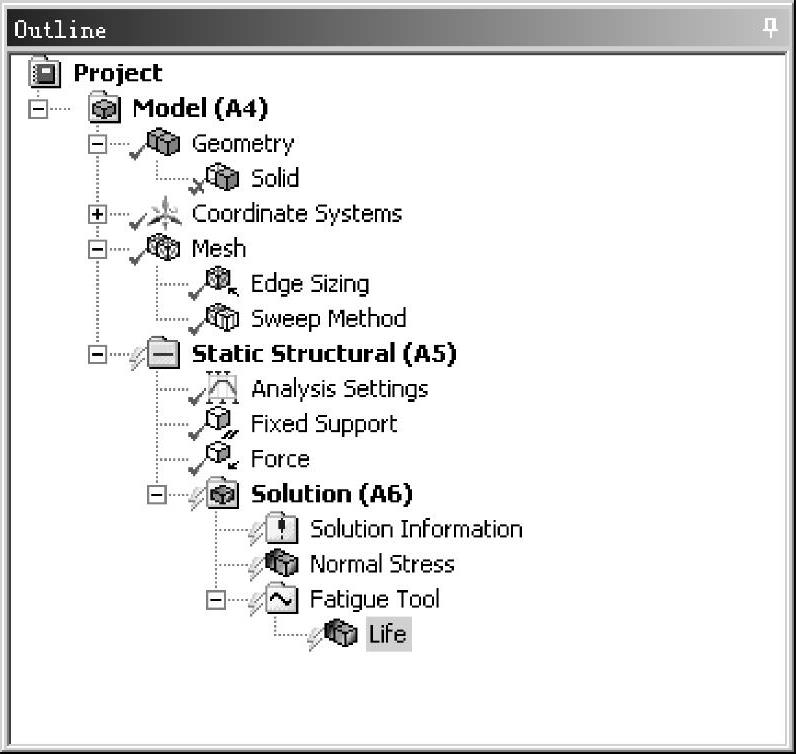
图9-41 分析结果在模型树中的位置

图9-42 设置疲劳分析方法

图9-43 X方向的正应力分析结果

用鼠标左键单击模型树中的Life，疲劳寿命分析结果如图9-44所示。

图9-44 疲劳寿命分析结果

7.结果分析

轴的最薄弱部位在中部，截面积为A=πr²=3.14×0.01²=3.14×10^-4 m²

危险部位应力为

上述应力分析结果与图9-43中ANSYS Workbench分析结果一致。对于疲劳寿命，有

a_p=19.8662，b_p=-6.2982所以

lgN_p=19.8662-6.2982×lg（300）=4.2648

N_p=10^4.2648=18399

与图9-44中ANSYS Workbench分析结果12974之差在同一个数量级内，计算结果合理。