车辆结构有限元分析：应力疲劳分析方法

基于ANSYS Workbench的应力疲劳分析如图9-4所示。需要强调的是图中所示分析流程是基于静力学分析结果的进一步分析。

1.S-N曲线

在整个应力疲劳分析流程中，第一步是定义S-N曲线，ANSYS Workbench中S-N曲线的定义是通过点定义的，如图9-5所示。要做好应力疲劳分析，需要深刻理解S-N曲线的基本概念，这样有助于读者理解疲劳分析的结果。明确S-N曲线的数学表达式，才能定义好S-N曲线，保证分析结果正确有效。

S-N曲线又被称为材料的疲劳性能，用于描述应力S和破坏时的寿命N之间的关系。在疲劳载荷作用下，最简单的载荷谱是恒幅循环应力。描述循环应力需要两个量：应力比R和应力幅S_a。如前所述，应力比是载荷谱的循环特性，应力幅是疲劳破坏的主要控制参量。在R=-1，对称恒幅循环载荷控制下，试验给出的应力-寿命关系，用S_a-N曲线表达，是材料的基本疲劳性能曲线。应力比R=-1时，有S_a=S_max，故基本应力-寿命曲线称S-N曲线。寿命N_f定义为在对称恒幅载荷作用下，直到结构被破坏的循环次数。

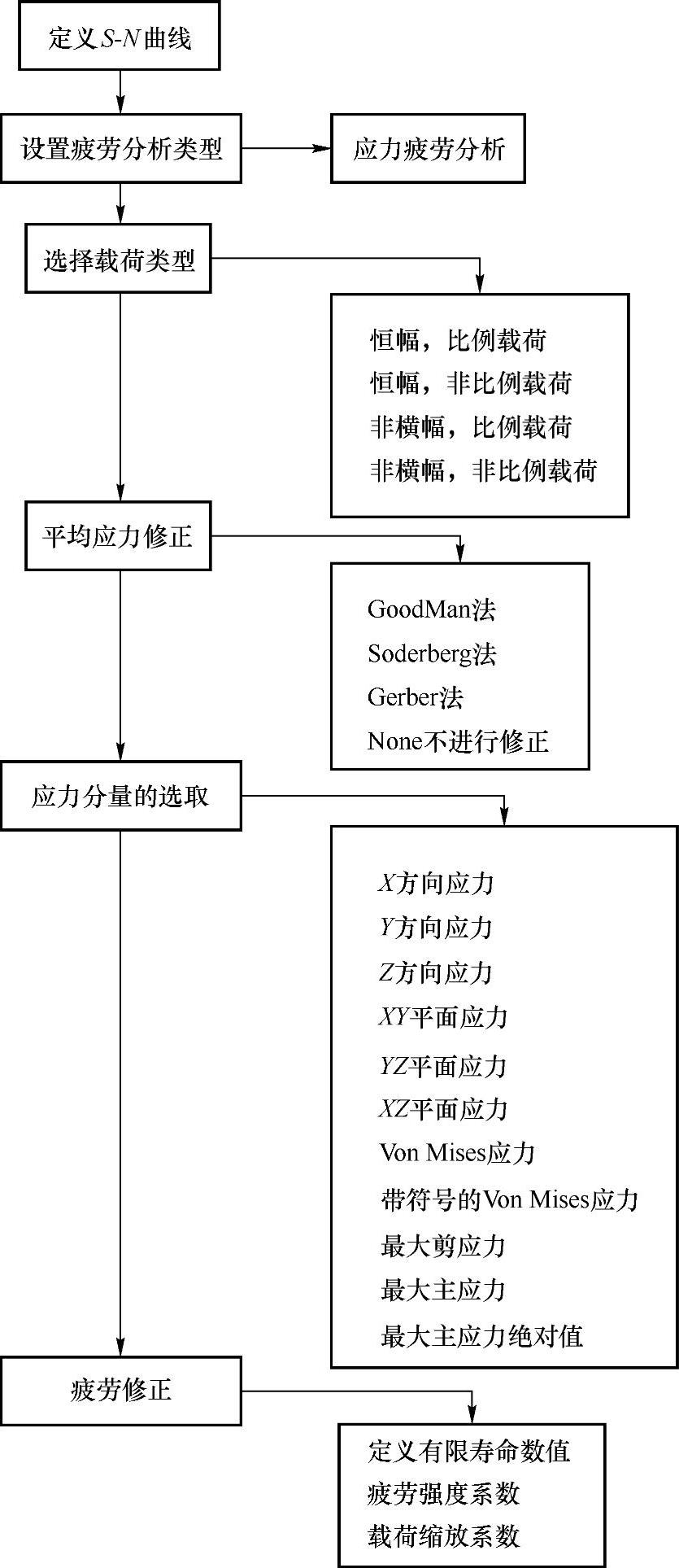
图9-4 ANSYS Workbench应力疲劳分析流程

疲劳破坏有裂纹萌生、稳定扩展和失稳扩展至断裂三个阶段，这里研究的是裂纹萌生寿命。因此，“破坏”可定义为：

1）标准小尺寸试件断裂。对于高、中强度钢等脆性材料，从裂纹萌生到扩展至小尺寸圆截面试件断裂的时间很短，对整个寿命的影响很小，考虑到裂纹萌生时尺度小，观察困难，这样定义是合理的。

2）出现可见小裂纹（如1mm），或有5%、15%应变降。对于延性较好的材料，裂纹萌生后有相当长的一段扩展阶段，不应当计入裂纹萌生寿命。小尺寸裂纹观察困难时，可以监测恒幅循环应力作用下的应变变化。当试件出现裂纹后，刚度改变，应变也随之变化，故可用应变变化量来确定是否萌生了裂纹。

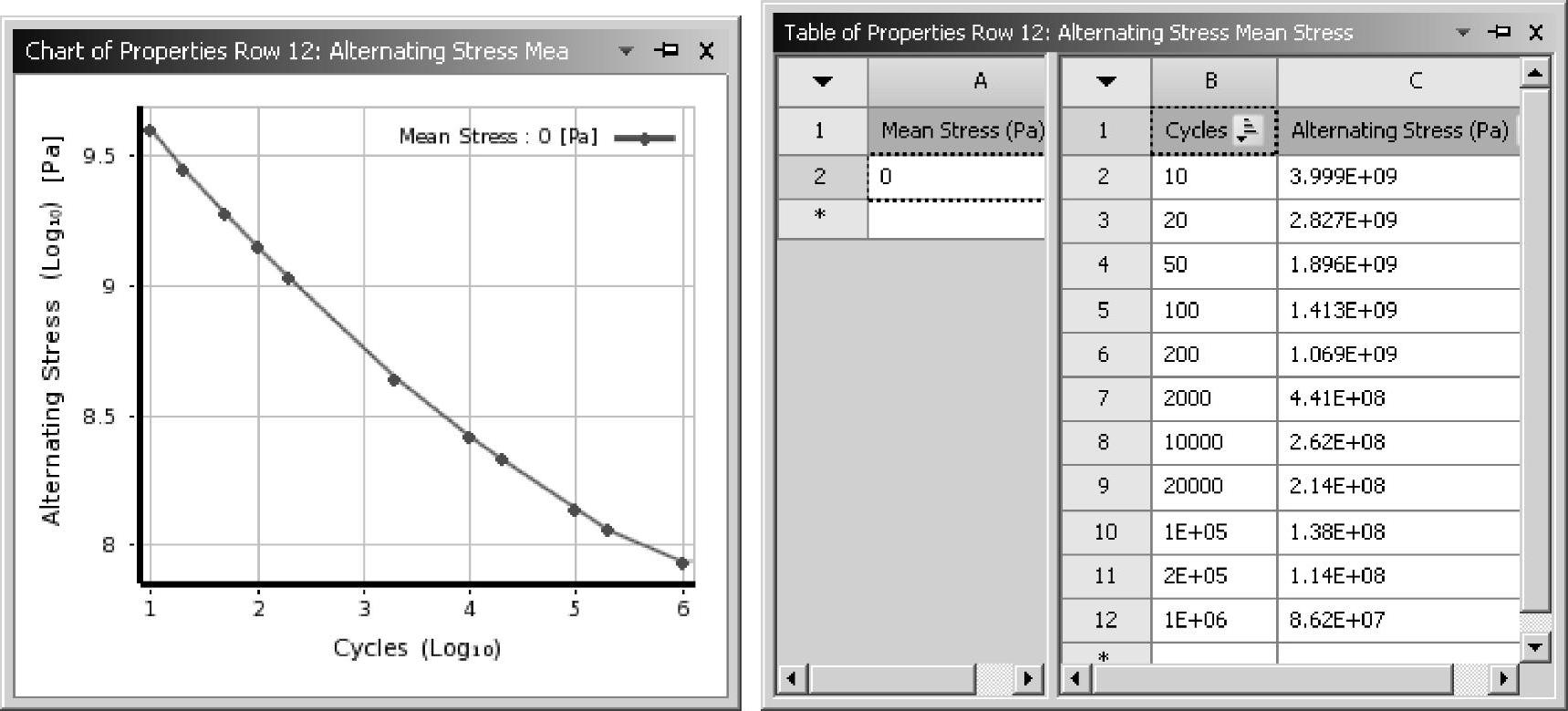
图9-5 ANSYS Workbench中S-N曲线的定义

材料疲劳性能试验所用标准试件一般是小尺寸（3～10mm）光滑圆柱试件。材料的基本S-N曲线，给出的是光滑材料在恒幅对称循环应力作用下的裂纹萌生寿命。用一组标准试件（通常为7～10件），在给定的应力比R下，施加不同的应力幅S_a进行疲劳试验，记录相应的寿命N，即可得到图9-6所示的S-N曲线。

从图9-6可以看出，在给定的应力比下，应力S（S_a或S_max）越小，寿命越长。当应力S小于某极限值时，试件不发生破坏，寿命趋于无限长。由S-N曲线确定的、对应于寿命N的应力，称为寿命为N循环的疲劳强度（Fatigue Strength），记作S_N。寿命N趋于无穷大时所对应的应力S记作S_f，称为材料的疲劳极限（Endur-ance Limit）。特别地，对应R=-1的对称循环下的疲劳极限，记作S_-1。

图9-6 S-N曲线

由于疲劳极限是由试验确定的，试验又不可能一直

进行下去，故所谓的“无穷大”一般被定义为：钢材，

10⁷次循环；焊接件，2×10⁶次循环；非铁金属，10⁸次循环。

满足S<S_f的设计，即无限寿命设计。

S_-N曲线的数学表达式有三种，熟悉这三种表达式有助于读者在ANSYS Workbench中定义S-N曲线，因为在软件中S-N曲线是用点定义的，需要利用这些数学表达式计算出点的坐标。

（1）幂函数式

描述材料S-N曲线的最常用形式是幂函数式，即

S^mN=C （9-1）

m与C是与材料、应力比、加载方式等有关的参数。两边取对数，有

lgS=A+BlgN （9-2）

式中，材料参数A=lgC/m，B=-1/m。式（9-2）表示应力S与寿命N间有对数线性关系，这一点，可由试验数据S、N在双对数图上是否线性而确定。

（2）指数式

指数形式的S-N曲线表达式为

e^mSN=C （9-3）

两边取对数后成为

S=A+BlgN （9-4）

式中，材料参数为A=lgC/m，B=-1/m。表示在寿命取对数、应力不取对数的图中，S与N间有线性关系，通常称为半对数线性关系。

（3）三参数式

有时希望在S-N曲线中考虑疲劳极限S_f，写成

（S-S_f）mN=C （9-5）

与（9-3）式、（9-4）式相比，式（9-5）中多了一个参数，即疲劳极限S_f，且当S趋近于S_f时，N趋于无穷大。

以上三种形式中，最常用的是幂函数式表达的S与N间的双对数线性关系。注意到S-N曲线描述的是高周应力疲劳，故使用下限为10³～10⁴，上限则由疲劳极限定义。

（4）S-N曲线的近似估计

描述材料疲劳性能的基本S-N曲线，应当由R=-1的对称循环疲劳试验给出，或查有关手册得到。在缺乏试验结果时，可依据材料强度S进行如下简单估计，供初步设计参考。

将已知金属材料的疲劳极限S_f与极限强度S_u的数据绘于图9-7中，发现可用斜线OA和水平线AB描述其关系。故对于一般常用金属材料，有图9-7所示的经验关系。

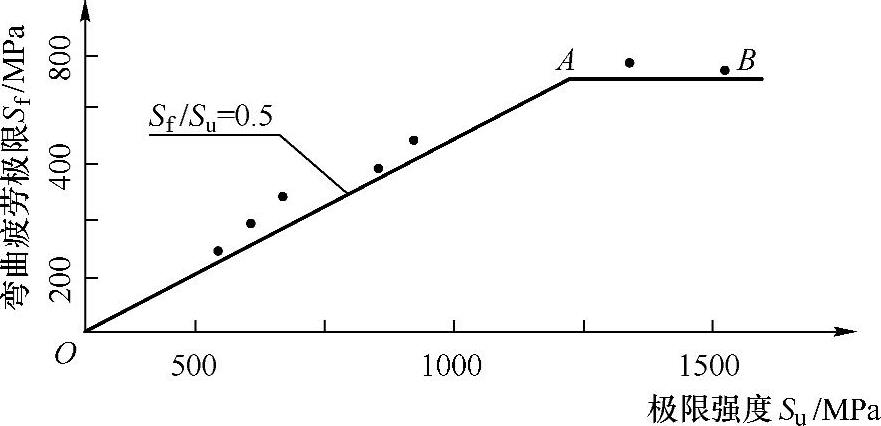
图9-7 弯曲疲劳极限与极限强度关系

R=-1时，旋转弯曲载荷作用下的疲劳极限可估计为

S_f（bending）=0.5S_uS_u<1400MPa （9-6）

S_f（bending）=700 MPa S_u≥1400MPa

不同材料旋转弯曲疲劳实验的结果表明，S_f（bending）为（0.3～0.6）S_u。

轴向拉压载荷作用下的疲劳极限可估计为

S_{f（tension）}=0.7S_{f（bending）}=0.35S_u （9-7）

不同材料的试验结果表明，S_{f（tension）}为（0.3～0.45）S_u。

承受对称扭转时有

S_{f（torsion）}=0.577S_f（bending）=0.29S_u （9-8）

试验结果表明：S_{f（torsion）}大多为（0.25～0.3）S_u。对于高强度脆性材料，极限强度S_u取值为极限抗拉强度；对于延性材料，S_u取值为屈服强度。

注意：

不同载荷作用形式下的疲劳极限和S-N曲线是不相同的。

若疲劳极限S_f和材料极限强度S_u为已知，S-N曲线可用下述方法作偏保守的估计。S-N曲线用双对数线性关系的幂函数形式（9-1）式表达，即

S^mN=C

寿命N=1时，S₁=S_u，即单调载荷作用下，试件在极限强度下破坏或屈服。考虑到S_-N曲线描述的是长寿命疲劳，不宜用于N<10³以下，故通常假定寿命N=10³时，有

S₁₀₃=0.9S_u （9-9）

对于金属材料，疲劳极限S_f所对应的循环次数一般为N=10⁷次，考虑到估计S_f时产生的误差，作如下偏于保守的假定：

N=10⁶时，S₁₀₆=S_f=kS_u （9-10）

式中，反映不同载荷作用形式的系数k，按照前述各式选取：弯曲时，k取0.5；拉压时，k取0.35；扭转时，k取0.29。

由S-N曲线可写出

C=（0.9S_u）m×10³=（kS_u）m×10⁶

依据上述二式可求得参数如下：

m=3/lg（0.9/k）；C=（0.9S_u）m×10⁶ （9-11）

如此估计的S-N曲线，只用于寿命为10³～10⁶之间的疲劳强度估计，超出此范围时不宜使用。

注意：

S-N曲线应由疲劳实验给出，任何形式的近似估计都只能供初步设计参考。

2.设置疲劳分析类型

如图9-4所示，应力疲劳分析的第二步就是要定义分析类型。在ANSYS Workbench中的疲劳分析类型选择中，有两个选项：一个是应力疲劳分析（Stress Life）；另一个是应变疲劳分析（Strain Life），如图9-8所示。

在应力疲劳分析过程中，疲劳寿命不再细分为裂纹形成寿命和裂纹扩展寿命，应力疲劳分析的计算结果即为整体寿命。一般来讲，应力疲劳分析的寿命结果都比较大，为10⁵循环次数以上。所以应力疲劳分析一直用于高周疲劳分析HCF（High Cycle Fatigue）或无限寿命分析。读者在利用ANSYS Workbench进行疲劳分析的过程中，可以参照这一原则选择分析类型。

3.载荷类型

如图9-4所示，应力疲劳分析的第三步是定义载荷类型。在应力疲劳分析过程中，AN-SYS Workbench提供了以下四种载荷类型（图9-9）供用户选择。

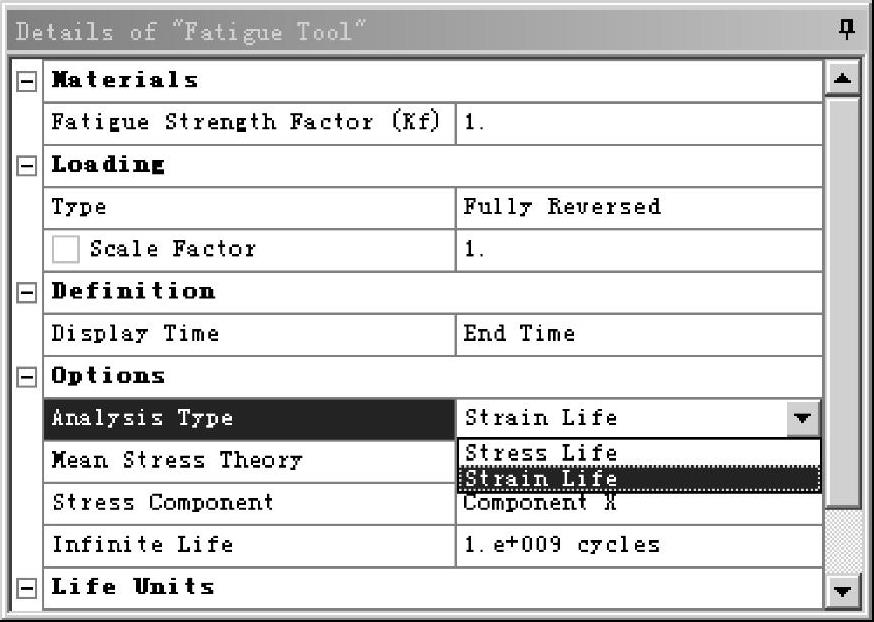
图9-8 设置疲劳分析类型

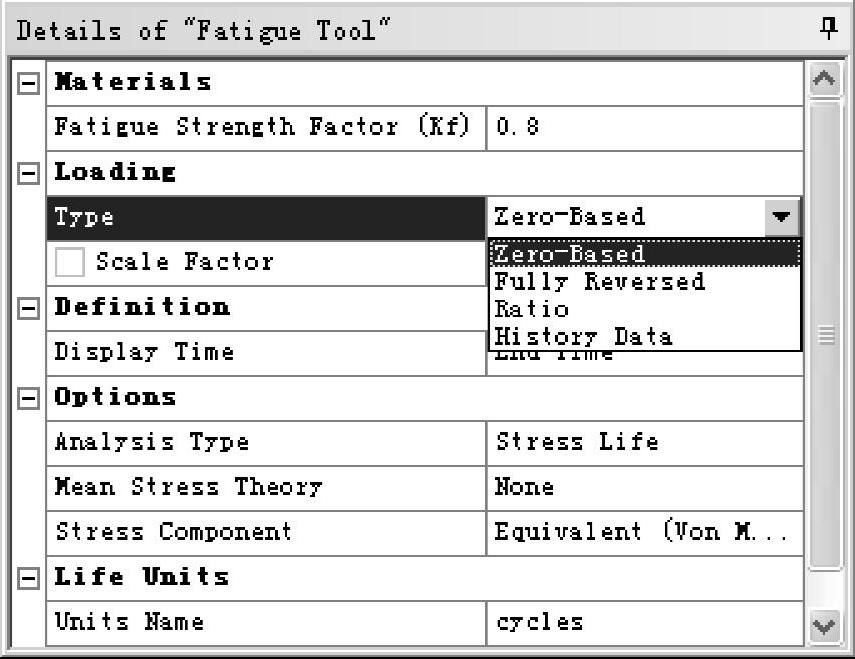
图9-9 ANSYS Workbench载荷类型选择

Zero-Based（R=0）：表示应力比为0的载荷（Constant Amplitude Load Zero-Based），如图9-10所示。

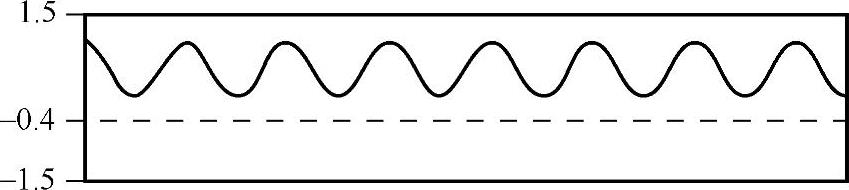
图9-10 Zero-Based载荷

Fully Reversed（R=-1）：表示应力比为-1的载荷（Constant Amplitude Load Fully Re-versed），如图9-11所示。

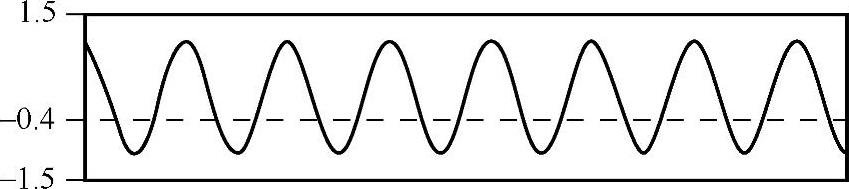
图9-11 Fully Reversed载荷

Ratio：指定应力比。

History Data：指定载荷时间历程。

前三种载荷都是恒定幅值比例载荷。第四种载荷是非恒定幅值比例载荷。

4.平均应力对疲劳寿命的影响

材料疲劳性能的S-N曲线，是在给定应力比R下得到的。R=-1的对称循环时的S-N曲线，是基本S-N曲线。平均应力对疲劳寿命的影响就是考虑应力比R的变化对疲劳寿命会产生影响，从而需要对S-N曲线进行修正。ANSYS Workbench提供了平均应力修正的五个选项，包括None、Goodman、Soderberg、Gerber和Mean Stress Curves，如图9-12所示。

各种平均应力修正方法在工作表（Worksheet）区通过曲线形象地表达出来，加粗的线条表示相应的修正方法，图9-13所示的直线表示不进行修正。

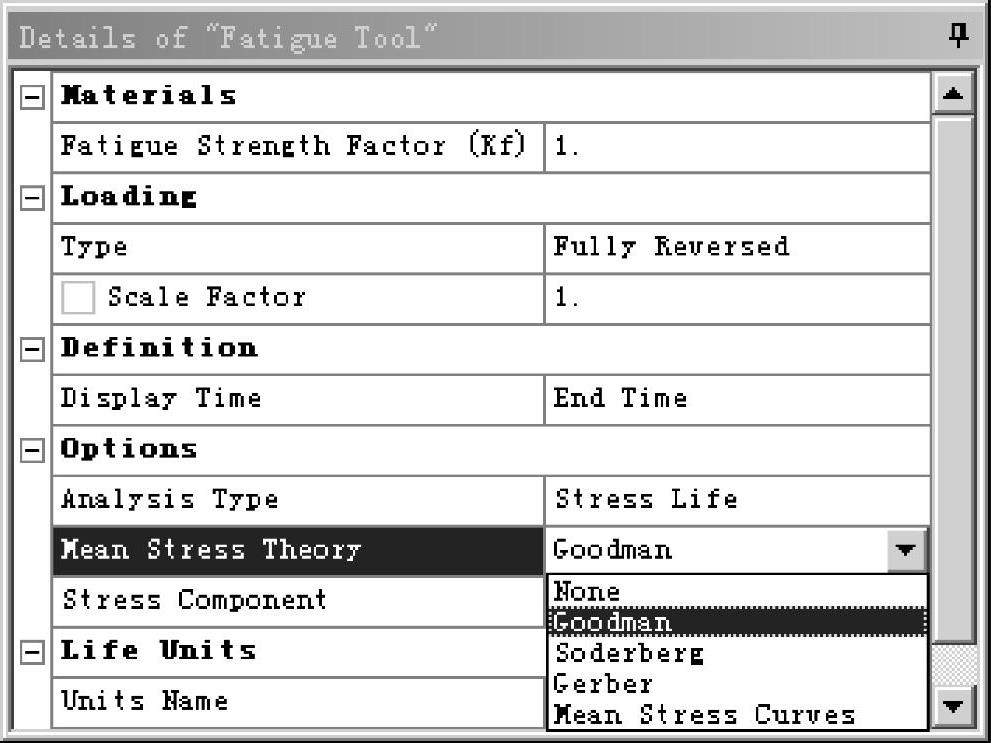
图9-12 平均应力修正选项

图9-13 平均应力None修正

（1）None修正（图9-13）

所谓None修正就是不需要进行平均应力修正。这一选项一般用在结构实际服役过程中的应力是应力比为-1的载荷，因为进行材料疲劳特性试验过程中所加载荷都是应力比为-1的载荷，所以不需要进行平均应力修正。

（2）Goodman修正

Goodman平均应力修正方法是应力疲劳常用的修正方法。如图9-12所示，选择Good-man选项，Worksheet区指示出Goodman平均应力修正方法的示意图，如图9-14所示。

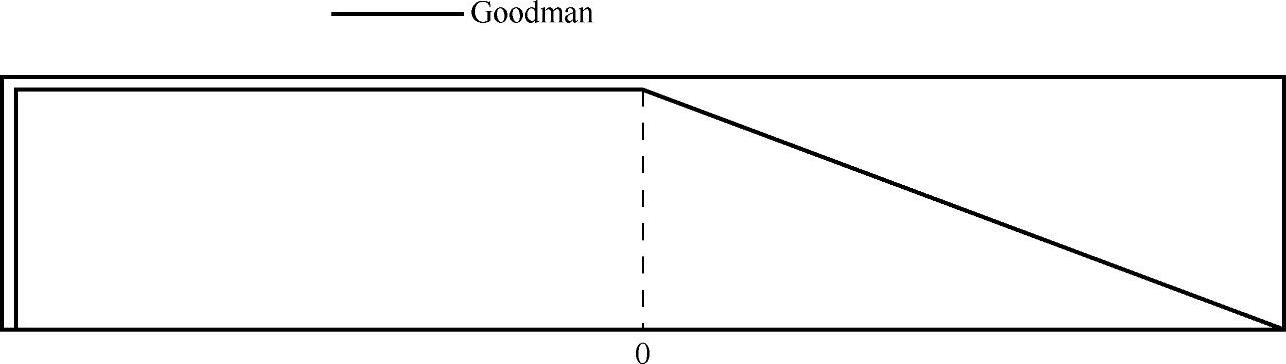
图9-14 平均应力Goodman修正

要深刻理解这一方法，首先需要知道应力比R的变化对疲劳性能的影响。由9.1.1给出的基本概念可知

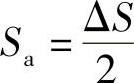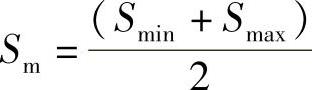应力幅值，平均应力，应力比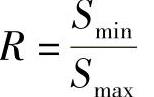

基于以上公式，可以推导得到平均应力与应力比之间的关系

从式（9-12）可以看出，应力比R增大，则循环平均应力S_m增大，可以理解为R的增大与减小，是平均应力增大或者减小的标志。故讨论应力比R对疲劳寿命的影响，实际上是讨论平均应力S_m对疲劳寿命的影响，当然这一讨论是建立在应力幅S_a不变的条件下。

当S_a给定时，R增大，平均应力S_m也增大，循环载荷中的拉伸部分增大，这对疲劳裂纹的萌生和扩展都是不利的，将使疲劳寿命N_f降低。平均应力对S-N曲线影响的一般趋势如图9-15所示。平均应力S_m=0时（R=-1）的S-N曲线是基本S-N曲线；当S_m﹥0，即拉伸平均应力作用时，S-N曲线下移，表示同样应力幅作用下的寿命下降，或者说结构在同样寿命下的疲劳强度降低，对疲劳有不利的影响；S_m<0，即压缩平均应力作用时，S-N曲线上移，表示同样应力幅作用下的寿命增大，或者说在同样寿命下的疲劳强度提高，压缩平均应力对疲劳的影响是有利的。因此，在实践中用喷丸、冷挤压和预应变等方法在高应力细节处引入残余压应力，是提高疲劳寿命的有效措施。(www.xing528.com)

在给定寿命N下，研究循环应力幅S_a与平均应力S_m之关系，可得到图9-16所示的结果。当寿命给定时，平均应力S_m越大，相应的结构疲劳强度S_a就越小；但无论如何，平均应力S_m都不可能大于材料的极限强度S_u。极限强度S_u为高强脆性材料的极限抗拉强度或延性材料的屈服强度。因此，等寿命条件下的S_a-S_m关系可以表达为

显然，当S_m=0时，S_a就是R=-1时的疲劳极限S_-1，当S_a=0时，载荷成为静载，在极限强度S_u破坏时，有S_m=S_u或S_m/S_u=1。

式（9-13）称为Goodman直线，所有的试验点基本都在这一直线的上方。直线形式简单，且在给定寿命下，由此作出的S_a-S_m关系估计偏于保守，故在工程实际中常用。利用上述关系，已知材料的极限强度S_u和基本S-N曲线，即可估计出在不同应力比或平均应力下的疲劳性能。

对比图9-14和图9-16，可以看出图9-16中的直线是图9-14中的正半轴部分，从图9-14可以看出，对于负半轴部分，也就是压缩应力为负的情况，不进行平均应力修正。

Goodman方法除了具有上述描述方法外，S_a和S_m还可以分别用疲劳极限S_-1和S_u进行归一化，形成图9-17所示的Haigh图。

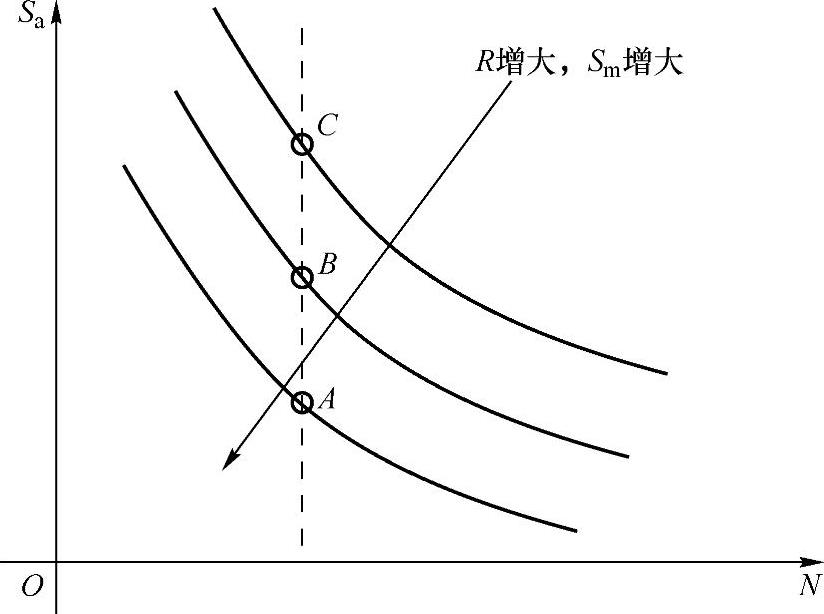
图9-15 平均应力的影响

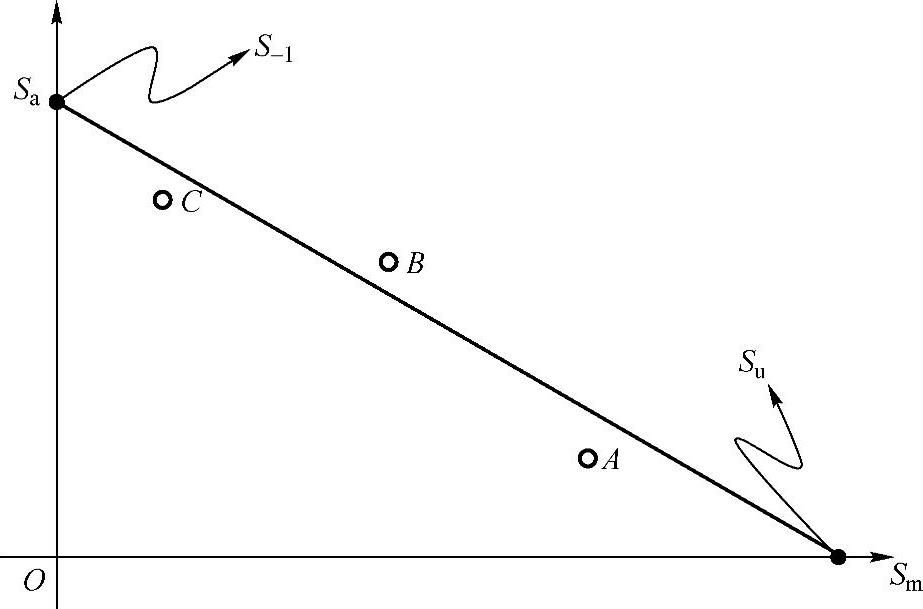
图9-16 S_a-S_m关系

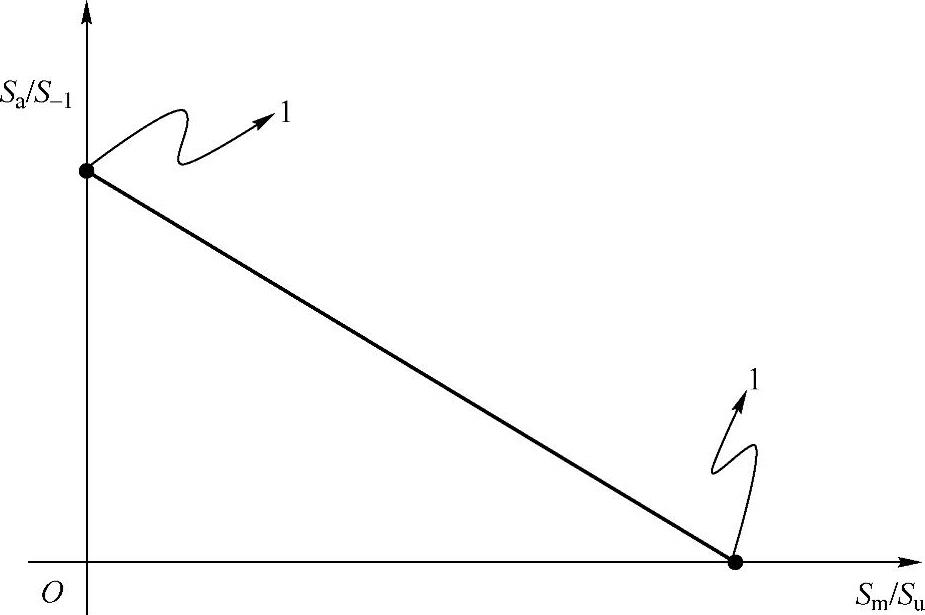
图9-17 Haigh图

（3）Gerber修正

如图9-12所示，选择Gerber选项，Worksheet区指示出Gerber平均应力修正方法的示意图，如图9-18所示。

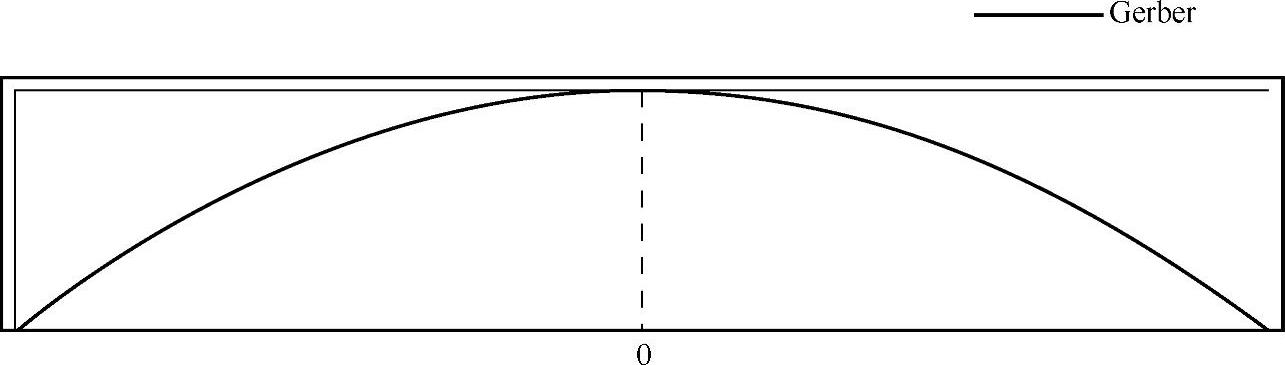
图9-18 Gerber修正方法

如果把平均应力和应力幅值间的关系用抛物线来描述，如图9-19所示，这种平均应力修正方法称为Gerber修正。Gerber修正方法见式（9-14）。

（4）Soderberg修正

Soderberg修正方法认为描述应力幅值与平均应力之间的关系是一条直线（图9-20），但是这条直线与横轴的交点为材料的屈服强度S_s。

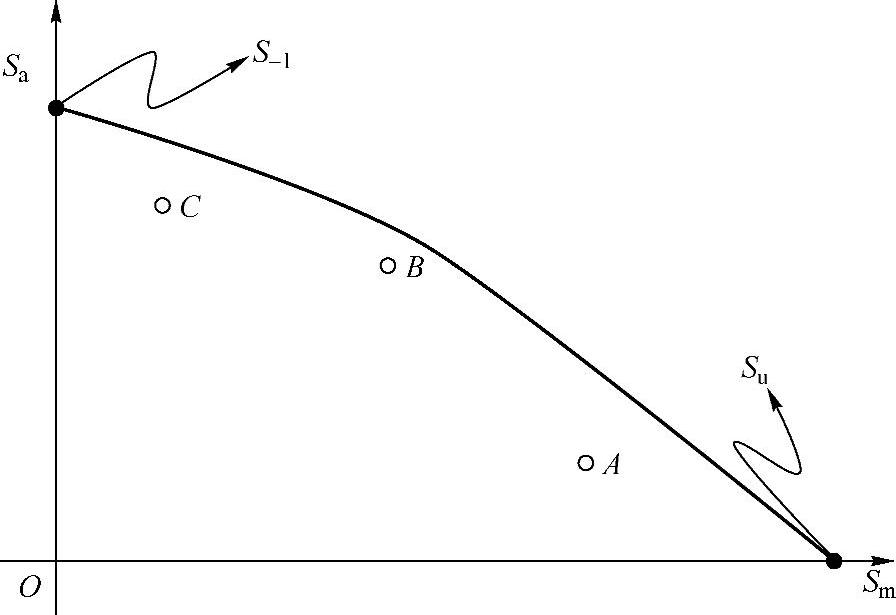
图9-19 Gerber抛物线

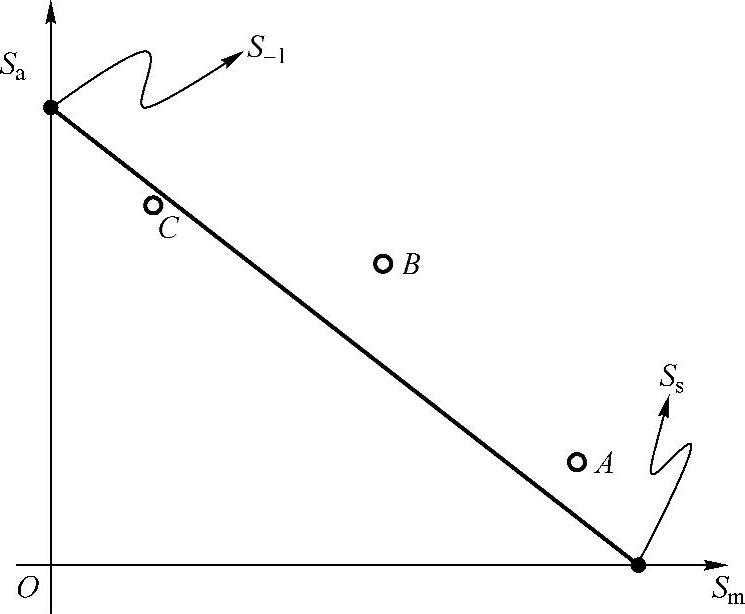
图9-20 Soderberg直线

如果结构在实际服役过程中受到的应力为（σ_a，σ_m），需要将其等效为（σ_-1，0）的载荷循环（因为材料的疲劳强度大都是标准试验件在平均应力为0、应力比为-1的条件下试验得到的），可以根据需要，采用不同的修正方法进行修正。

采用Goodman修正方法，用σ_a代替式（9-13）中的S_a，用σ_m代替公式中的S_m，S_u为已知，则

其他平均应力修正方法的应用和Goodman方法相同，这里不再赘述。

5.疲劳强度系数K_f

K_f是疲劳强度系数，又称为疲劳强度缩减系数（fatigue strength reduction factor）。在进行应力疲劳分析中，通过这一系数对S-N曲线进行调整。通常疲劳强度系数用于反映表面加工状态等因素对疲劳强度的影响，这一参数的选择可以参考相关手册。

6.应力分量的选取

在进行结构应力分析的过程中，得到的是多轴应力，但是试验过程中得到的一般是单轴应力。在ANSYS Workbench的应力疲劳分析过程中，可以选择X、Y、Z三个方向的应力分量，Von Mises应力，带符号的VonMises应力（将绝对值最大主应力的符号作为Von Mises应力的符号）等，如图9-21所示。在考虑压缩平均应力对疲劳寿命的影响中，带符号的Von Mises应力是非常有用的。

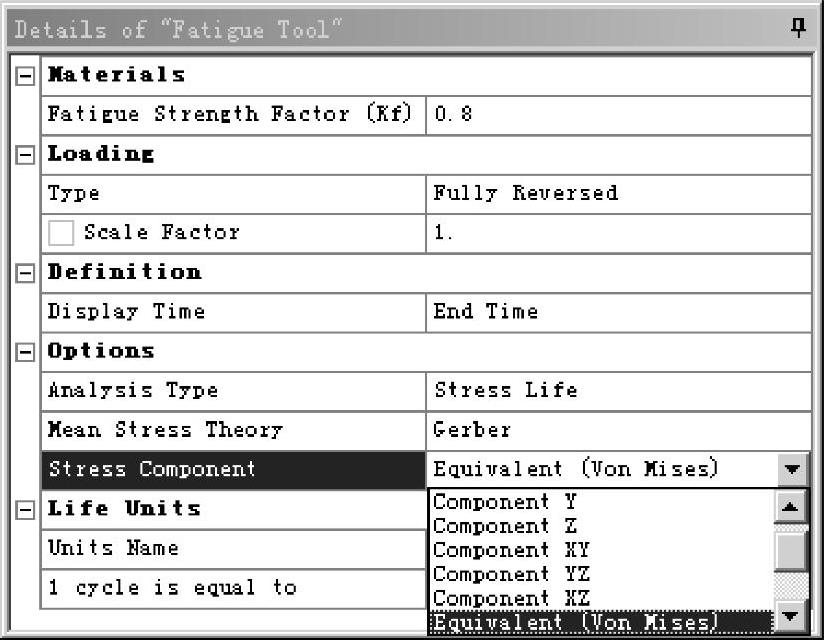
图9-21 应力分量的选取

7.载荷谱

进行疲劳分析时，首先必须确定零部件或结构工作状态下所承受的载荷谱。载荷谱的确定通常有两种方法：一是借助于已有的类似构件、结构或其模型，在使用条件或模拟使用条件下进行测量，得到各典型工况下的载荷谱，再将各工况组合起来得到的载荷谱，称为实测载荷谱；二是在没有适当的类似结构或模型可用时，依据设计目标分析工作状态，结合经验估计载荷谱，这样给出的是设计载荷谱。

例如，有一台商用汽车，设计寿命500000km，前轴上的设计承载为70kN，下面推导前车轮轮轴的设计载荷谱。

轮轴承受的静态垂直力F_v，stat为70/2=35kN，因前轴有两个车轮，各承载50%。

（1）直线行驶的动态载荷谱

垂直动态力：

取动态系数为2.28，则垂直动态力为35kN×2.28=80kN。

侧向动态力F_y：

F_y=F_v，stat×0.35≈12kN

纵向动态力：

F_x=F_v，stat×0.5≈18kN

（2）转弯行驶的最大动态力

侧向动态力F_y：

F_y=F_v，stat×1.5≈52kN

纵向动态力F_x：

F_x=F_v，stat×0.9≈31kN

（3）制动行驶的最大动态力

制动时最大垂直力：

F_v=F_v，stat×2.2=77kN

制动时最大纵向力：

F_x=F_v，stat×1.4=49kN

在上述力的作用下，轮轴的关键部位的最大应力幅值应力比确定如下。设计寿命500000km，每1km轮轴转动300次，故总循环次数为500000×300=1.5×10⁸。

直线行驶：0.96×1.5×10⁸=1.44×10⁸

转弯行驶：0.02×1.5×10⁸=3×10⁶

制动：1.5×10⁸-1.44×10⁸-3×10⁶=3×10⁶

通过有限元计算，得到车辆的直线行驶、转弯行驶、制动三种工作状态下的应力和循环次数。该车轮轴的应力载荷谱见表9-1。

表9-1 某商用汽车应力载荷谱

表9-1为简单的应力载荷谱的表达方式。

8.Miner线性累积损伤理论

对载荷谱（载荷时间历程）计数，可得到图9-22所示的载荷（S）-循环次数（n）图。

若构件在恒幅应力水平S作用下，循环至破坏的寿命为N，则可定义它在经受n次循环时的损伤为

D=n/N （9-17）

显然，在恒幅应力水平S作用下，若n=0，则D=0，构件未受疲劳损伤；若n=N，则D=1，构件发生疲劳破坏。

构件在应力水平S_i作用下，经受n_i次循环的损伤为D_i=n_i/N_i。若在k个应力水平S_i作用下，各经受n_i次循环，则其总损伤为

D=∑^kD_i=∑n_i/N_i（i=1，2，…，k） （9-18）

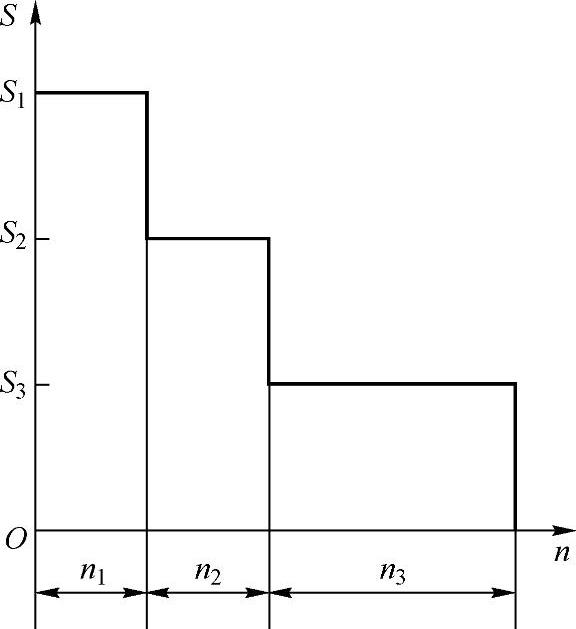
图9-22 变幅载荷谱

破坏准则为

式中，n_i是在S_i作用下的循环次数，由载荷谱给出；N_i是在S_i作用下循环到破坏的寿命，由S-N曲线确定。

式（9-19）就是最简单、使用最广泛的Miner线性累积损伤理论。

图9-23给出了构件在最简单的变幅载荷（两水平载荷）下的累积损伤。从图中坐标原点出发的射线，是给定应力水平S_i下的损伤线。注意到N_f是由S-N曲线确定的常数，则损伤D与载荷作用次数n的关系可由式（9-19）的线性关系来描述。因此，上述Miner累积损伤理论是线性理论。图中，构件在应力水平S₁下经受n₁次循环后的损伤为D₁，再在应力水平S₂下经受n₂次循环，损伤为D₂，若总损伤D=D₁+D₂=1，则构件发生疲劳破坏。

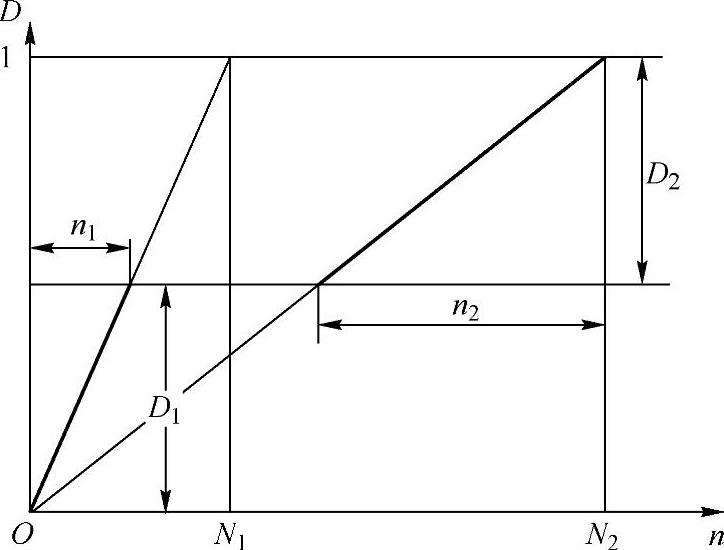
图9-23 线性累积损伤

由式（9-19）还可看出，Miner累积损伤与载荷S_i作用的先后次序是无关的。利用Miner理论进行疲劳分析的一般步骤为：

1）确定构件在设计寿命期的载荷谱，选取拟用的设计载荷或应力水平。

2）选用适合构件使用的S-N曲线（通常需要考虑构件的具体情况，对材料S-N曲线进行修正而获得）。

3）再由S-N曲线计算其损伤，D_i=n_i/N_i，按式（9-19）计算总损伤D。

4）判断是否满足疲劳设计要求。若在设计寿命内的总损伤D<1，构件是安全的；若D﹥1，则构件将发生疲劳破坏，应降低应力水平或缩短使用寿命。

例如，已知构件可用的S-N曲线为S²N=2.5×10¹⁰，如图9-24所示；设计寿命期的载荷谱如表9-2中前两栏所列。试估计该构件可承受的最大应力水平。

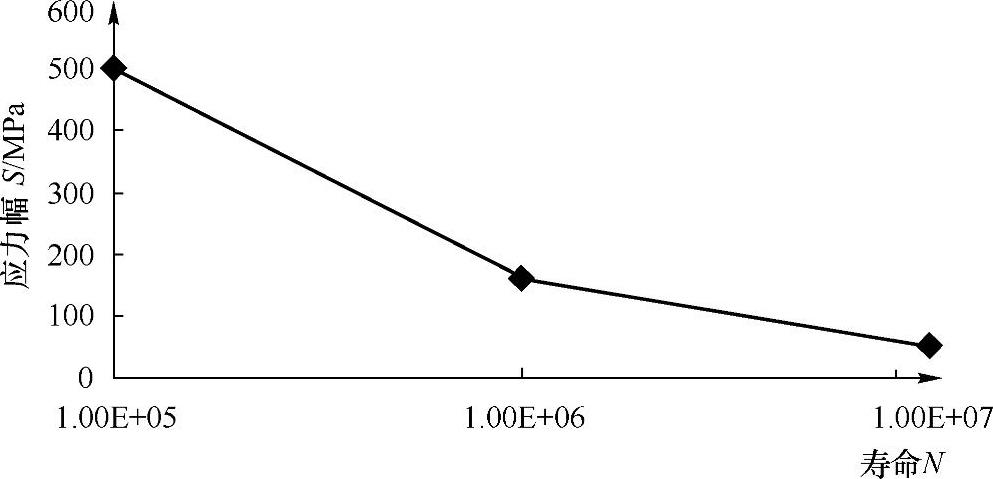
图9-24 S-N曲线

假定对应于100%载荷P时的应力S=200MPa，其余各级载荷对应的应力水平列于表中第三栏。

表9-2 构件设计载荷谱

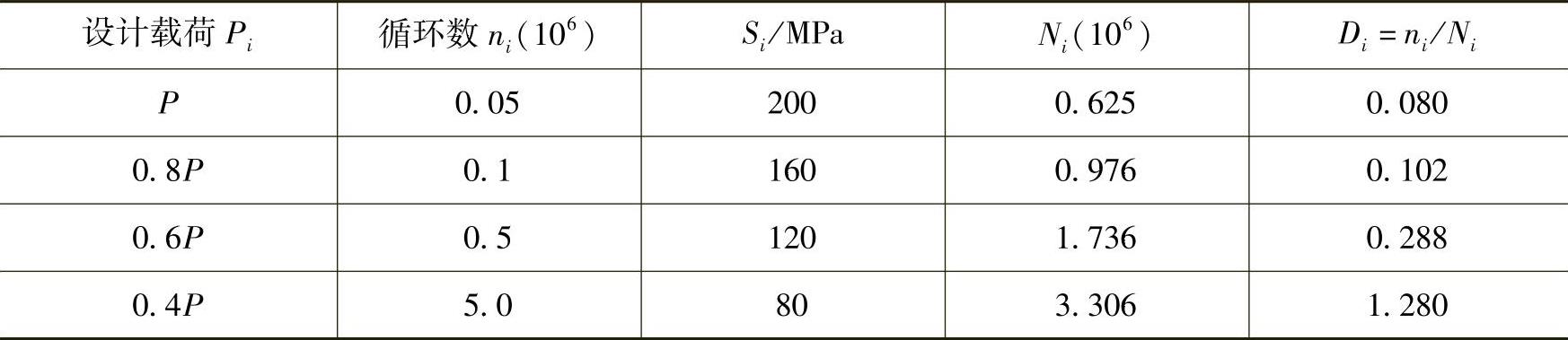
再由S-N曲线得到在各恒幅应力循环下的寿命N_i，如表中第四栏所列。计算各级应力下的损伤，列于表中第五栏。求得的总损伤为∑D_i=∑n_i/N_i=1.75。

由上述计算结果可知，若选取应力S=200MPa，则在设计寿命内总损伤D=1.75﹥1，构件将发生疲劳破坏。因此，需要降低所选取的应力水平，重新计算。

再取应力S=150MPa，计算结果为：D=∑D_i=∑n_i/N_i=0.985<1，构件能够达到设计寿命。故S=150MPa，基本上是构件可承受的最大应力水平。

某构件的S-N曲线为S²N=2.5×10¹⁰，若它一年内所承受的典型应力谱如表9-3中前两栏所列，试估计其寿命。

表9-3 典型应力谱及其损伤计算

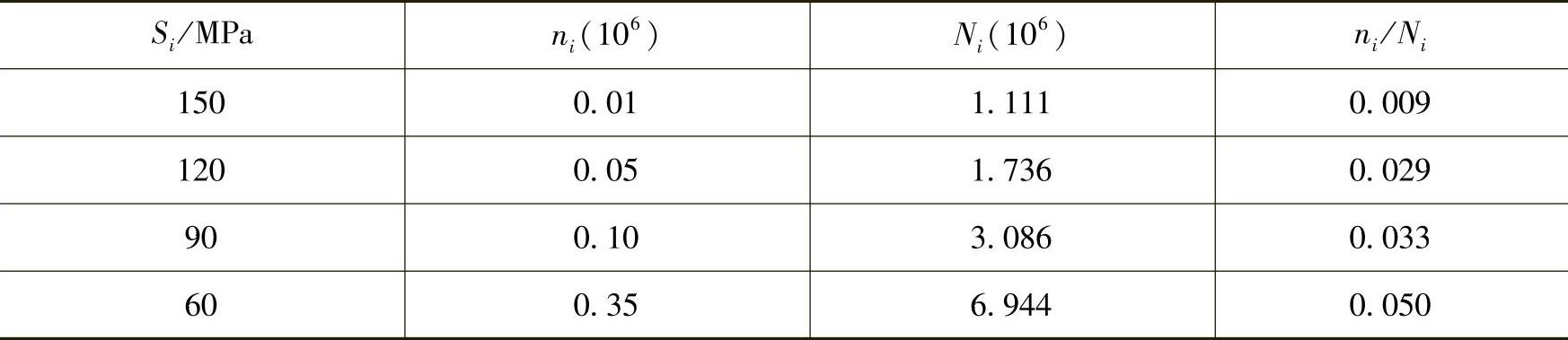
如前所述，如果构件的使用可以以年为周期，则可由此形成构件的典型应力谱，其后各年所承受的循环载荷，是该典型应力谱的重复。若将典型应力谱作为一个循环块，损伤为∑n_i/N_i，整个寿命有λ个循环块，则总损伤应为

D=λ∑n_i/N_i

按照Miner理论，疲劳破坏的判据为

D=λ∑n_i/N_i=1 （9-20）

由表9-3中计算结果可知，该构件一年内形成的损伤为∑n_i/N_i=0.121，故由式（9-20）有

λ=1/∑（n_i/N_i）=（1/0.121）年=8.27年