车辆结构模态分析-车辆结构有限元分析

在ANSYS Apdl操作平台上，模态分析的操作步骤与在ANSYS Workbench平台上相同：①建立一个工程项目；②修改材料数据；③建立/导入几何模型；④建立有限元模型，包括划分网格、施加载荷；⑤进行求解；⑥查看分析结果。首先启动ANSYS Apdl，如图6-21所示。

图6-21 启动ANSYS Apdl

1.建立一个模态分析项目

（1）进入前处理器

选择菜单GUI：Preprocessor。

命令：/PREP7。

（2）添加标题

选择菜单GUI：Utility Menu﹥File﹥Change Title...。

新标题为：Modal Analysis。

命令：/TITLE，Modal Analysis。

（3）修改工作名

选择菜单GUI：Utility Menu﹥File﹥Change Jobname...。

键入工作名：Modal。

命令：/FILNAME，Modal，0。

（4）选择分析类型

确定分析类型为模态分析，选择菜单GUI：Solution﹥Analysis Type﹥New Analysis﹥Mo-dal。

命令：ANTYPE，2。

（5）定义单位制

在命令行输入/units，si，然后单击回车键，定义单位为国际单位制，即长度：m；力：N；压强/压力：Pa；面积：m²；质量：kg。

2.定义材料属性

（1）定义各向同性线性材料

GUI：Preprocessor﹥Material Props﹥Material Models﹥Structural﹥Linear﹥Elastic﹥Isotrop-ic，弹出窗口如图6-22所示。

键入的材料参数如下：

弹性模量（Young s modulus EX）：2.068e11。

泊松比（PRXY）：0.3。

命令：

MP，EX，1，2.068e11。

MP，PRXY，1，0.3。

（2）定义材料密度

GUI：Preprocessor﹥Material Props﹥Material Models﹥Structural﹥Density弹出窗口如图6-23所示。

图6-22 定义弹性模量和泊松比

图6-23 定义材料密度

输入密度值“7830”，如图6-23所示，单击OK按钮。

命令：

MP，DENS，1，7830。

注意：

在动态分析过程中，材料的密度和弹性模量都必须进行准确定义

3.建立几何模型

（1）定义关键点（梁的端点）

选择菜单GUI：Preprocessor﹥Modeling﹥Create﹥Keypoints﹥In Active CS，弹出如图6-24所示的对话框，按照如图所示进行设置。

图6-24 定义梁的左侧端点

单击Apply按钮，接下来定义关键点2，如图6-25所示，单击OK按钮，完成右侧端点定义。

图6-25 定义梁的右侧端点

命令：

定义1#关键点：k，1，0，0。

定义2#关键点：k，2，1，0。

（2）定义直线（梁的实体模型）

通过关键点定义直线（悬臂梁模型），选择菜单GUI：Preprocessor﹥Modeling﹥Create﹥Lines﹥Lines﹥Straight Line，单击鼠标左键拾取图形界面上的两个关键点，然后单击鼠标中键确认，在1#和2#关键点之间生成一条直线。

命令：L，1，2。

4.建立有限元模型

（1）选择单元

1）定义单元。选择菜单GUI：Preprocessor﹥Element Type﹥Add/Edit/Delete...，弹出如图6-26所示的对话框。

选择BEAM3（二维弹性梁）单元，如图6-26所示，单击OK按钮。

命令：ET，1，BEAM3。

2）定义实常数。选择菜单GUI：Preprocessor﹥Real Constants﹥Add，弹出BEAM3实常数窗口（Real Constants for BEAM3），如图6-27所示。

由于采用国际单位制，相关参数的计算一定要基于国际单位进行计算，通过计算，填写后如图6-27所示。

梁横截面面积

面积=0.01×0.01=0.0001m²

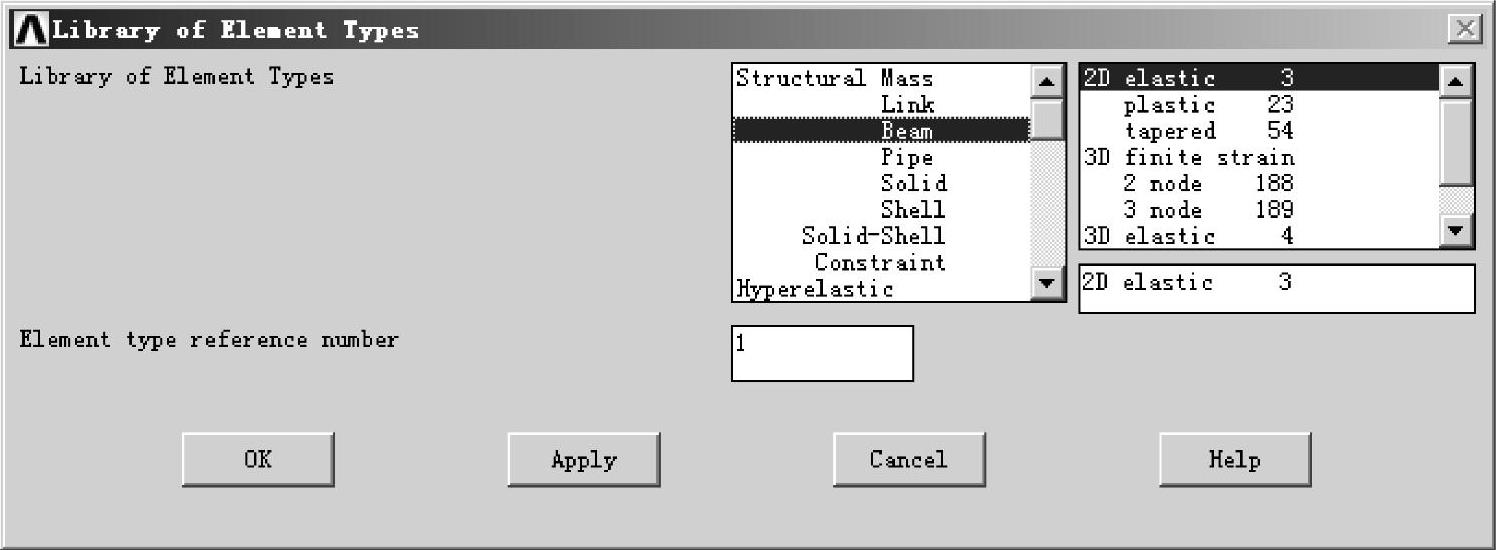
图6-26 定义单元

截面惯量

截面惯量(www.xing528.com)

命令：R，1，0.0001，833.33333，0.01。

（2）生成网格

1）设定网格尺寸。选择菜单GUI：Preprocessor﹥Meshing﹥Size Cntrls﹥ManualSize﹥Lines﹥All Lines...，弹出如图6-28所示的对话框。

按照如图6-28所示进行设置，将悬臂梁模型分为10份，即单元长度为100mm。

命令：LESIZE，ALL，，，10。

图6-27 定义BEAM3实常数

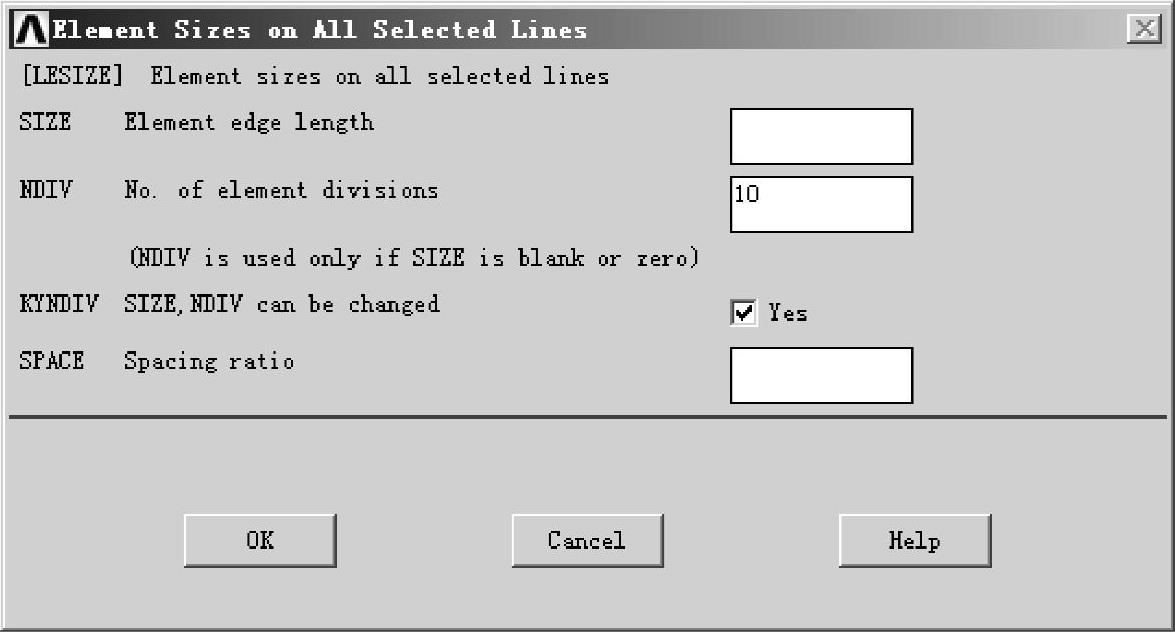
图6-28 定义网格尺寸

2）划分网格。选择菜单GUI：Preprocessor﹥Meshing﹥Mesh﹥Lines﹥Pick All。

命令：LMESH，1。

（3）施加载荷/约束

在关键点（梁的端点）定义位移约束，选择菜单GUI：Solution﹥Define Loads﹥Apply﹥Structural﹥Displacement﹥On Keypoints，在弹出的对话框选择1#关键点，固定（Fix）1#关键点所有自由度（ALL DOFs）。

5.定义模态求解参数

打开分析类型选项窗口。选择菜单GUI：Solution﹥Analysis Type﹥Analysis Options...，弹出如图6-29所示的对话框。

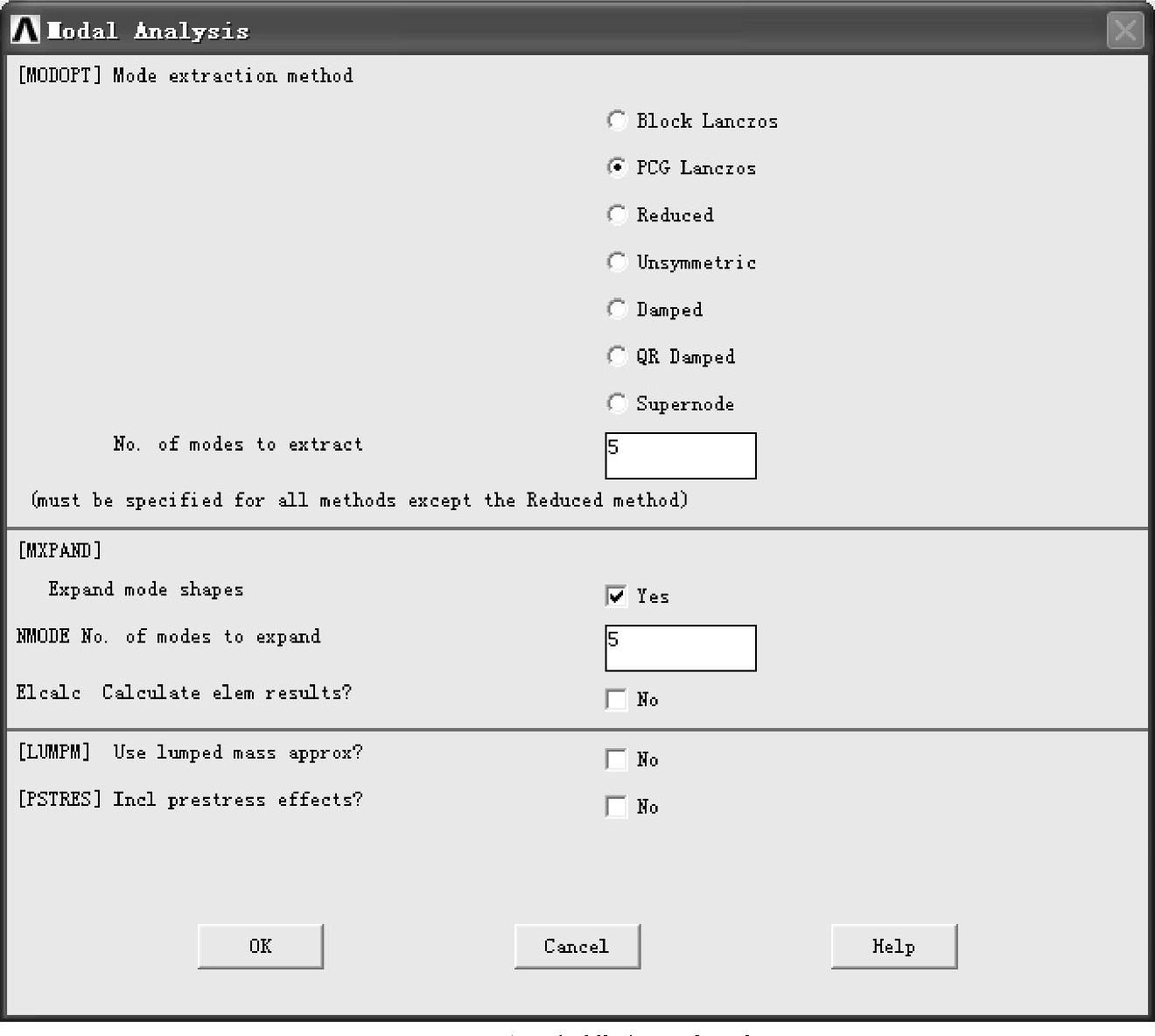
图6-29 设定模态分析选项

（1）Mode Extraction Method各选项的含义

1）子空间法。子空间法（Subspace）适用于大型对称矩阵特征值问题求解。可以通过采用多种求解控制选项来控制子空间迭代过程，获取比较精确、可信的解。

2）Block Lanczos法。Block Lanczos法主要应用于大型对称矩阵特征值问题求解。

3）Power Dynaimics法。Power Dynaimics法适用于非常大的模型，即自由度数超过10万的模型求解。此法在求解前几阶模态方面精度非常高，可以用来求解结构前几阶模态，了解结构可能的响应情况，然后再采用适用于高阶求解的方法，如子空间法或者Block Lanczos法进行高阶求解。

4）Unsymmetric法。Unsymmetric法用于系统矩阵为非对称矩阵问题求解，如流体—结构耦合问题。

5）Damped法。Damped法用于阻尼作用不可以忽略问题类型的求解，如轴承问题等。对于大多数问题而言，子空间法和Reduced法、Block Lanczos法或者Power Dynaimics法基本够用了，其他两种方法只有在很特殊情况下才可能用到。知道模态提取方法后，ANSYS自动选择合适的求解器。

（2）MXPAND选项

此选项在采用Reduced法、Unsymmetric法和Damped法时才需要设置。但是如果想得到单元求解结果，则不论哪种模态提取方法都需要扩展计算单元结果选项。

（3）Prestress Effect Caculation选项

此选项适合于有预应力结构的模态分析。一般采用默认设置时不考虑预应力。

在本例题中选择子空间法（PCG Lanczos），并在提取几阶模态输出（No.of modes to ex-tract）栏键入“5”。启用模态图形展开（Expand mode shapes）选项，模态展开阶数（No.of modes to expand）栏中键入“5”阶，单击OK按钮。注意到ANSYS系统默认设置为简化法（Reduced Method）。简化法是几种方法中速度最快的，因为它只考虑所有自由度中起到主要作用的自由度。而子空间法（Subspace Method）考虑所有自由度，因此，子空间法更精确，但是需要耗费更多计算时间（尤其是几何形状比较复杂时）。

定义子空间模态分析选项，按如图6-30所示对话框进行设置，然后单击OK按钮。

图6-30 子空间法模态分析定义

6.求解

选择菜单GUI：Solution﹥Solve﹥Current LS。

命令：SOLVE。

7.查看分析结果

（1）查看各阶模态对应频率

选择菜单GUI：General Postproc﹥Results Summary，弹出SET，LIST Command的对话框（如图6-31所示），显示出子空间法的分析结果。

图6-31 模态分析结果列表

注意：

为了获取精确的高阶模态频率，网格需要划分得更加细密，也就是说，划分网格不应该是现在的10份而是15份或者更高，具体情况依读者所关心的最高模态阶数确定。

（2）查看各阶模态图形

1）首先读入结果。取第一阶模态结果，选择菜单GUI：General Postproc﹥Read Results﹥First Set。

2）显示变形后图形。选择菜单GUI：General Postproc﹥Plot Results﹥Deformed shape。

选择Def+undef edge选项，则第一阶模态将显示在图形对话框（图6-32）。

3）查看下一阶模态形状。选择菜单GUI：General Postproc﹥Read Results﹥Next Set。

显示变形后图形，选择菜单GUI：General Postproc﹥Plot Results﹥Deformed shape，在弹出对话框选择Def+undef edge选项。

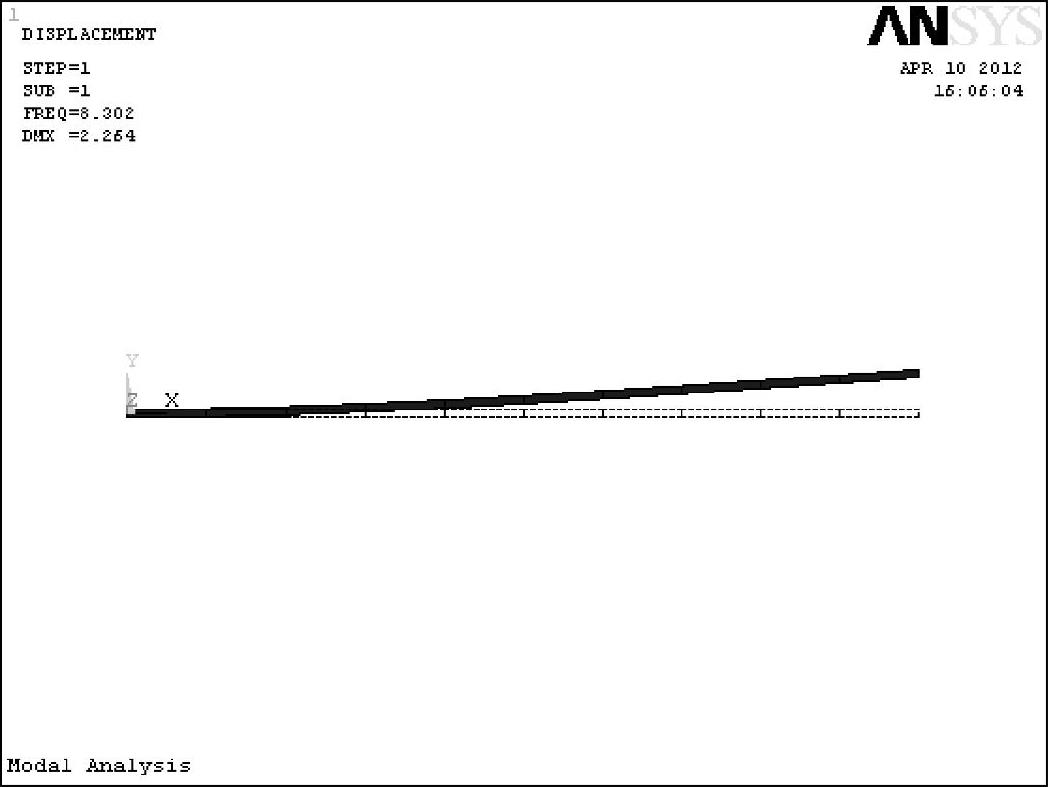
图6-32 第一阶模态

4）第一阶到第四阶模态图形。重复步骤3）得到第一阶到第四阶模态图形如图6-32～图6-35所示。

第一阶模态如图6-32所示。

第二阶模态如图6-33所示。

第三阶模态如图6-34所示。

第四阶模态如图6-35所示。

5）显示模态动画。通过菜单操作打开动画设置对话框，GUI：Utility Menu﹥Plot Ctrls﹥Animate﹥Mode Shape，弹出Animate Mode Shape对话框（图6-36）。保持默认设置并单击OK按钮。

表6-1为理论分析值与ANSYS解对比，从表中对比可以看出，三者差异不大。

图6-33 第二阶模态

图6-34 第三阶模态

表6-1 计算结果与理论值对比

图6-35 第四阶模态

图6-36 显示模态动画