有限元分析|车辆结构

一般而言，有多种方法可用于推导有限元问题的公式，其中包括直接法、最小总势能法、加权余数法。这里有必要指出，无论怎样建立有限元模型，有限元分析的基本步骤都与以上列举的步骤相同。这里通过举例说明介绍直接法。

假设有一端承受载荷P的变截面杆，如图2-1所示。杆一端固定，另一端承受载荷P。以w₁代表杆的上端宽度，w₂代表杆的下端宽度，杆的厚度为t，长度为L，杆的弹性模量用E表示。当杆件承受载荷P时，沿杆长度方向上有不同大小的变形。求在载荷P作用下，杆末端的位移。在以下的分析中，假设应用的载荷比杆的重量要大得多，因此忽略杆的重量。

1.前处理阶段

（1）将求解域离散成有限个单元

首先将问题分解成节点和单元。为突出有限元分析的基本步骤，仅用5个节点和4个单元来表示整个杆，如图2-2所示。不过，需要说明的是，使用的节点和单元数越多，结果可能越精确。这个任务留给读者作为练习来完成。给定杆的模型中有4个独立的部分，每个部分均有一个统一的横截面（图2-3）。每个单元的横截面积，由构成单元节点处的横截面的平均面积表示。

（2）假定一个近似描述单元特性的解

为了研究典型单元的力学特性，不妨先考虑横截面积为A、长度为l的杆件在外力F作用下构件的变形。

构件的平均应力由下式给出：

图2-1 承受轴向载荷的杆

构件的平均正应变ε定义为每单位原始长度l与受力前后长度变化Δl的比值：

（3）建立刚度矩阵

图2-2 将杆离散成节点和单元

图2-3 受外力P作用的等截面杆

在弹性区域内，应力和应变服从胡克定律，根据胡克定律有

σ=Eε （2-4）

式中，E是材料的弹性模量。

联立式（2-2）、式（2-3）和式（2-4）并简化后，有

注意：式（2-4）和常用的弹簧方程F=kx很相似。因此，受轴向力作用的等截面杆可以看做是一个弹簧，其等价刚度为

注意，本例中杆件的截面面积在y方向上是变化的。作为一次近似，可以将杆看做是由4个弹簧串联起来的模型。根据式（2-4），在i和i+1节点处，单元的弹性特性可以由相应的弹簧模型描述，即有如下方程：

这里等价的弹簧单元的刚度由下式给出

式中，A_i和A_i+1分别是i和i+1处节点的横截面面积；l是单元的长度。

利用以上模型，假定力施加在各个节点上。图2-4描述了模型中节点1～节点5的受力情况。

静力平衡条件要求每个节点上的力的总和为零，这会产生如下5个方程：

节点1：R₁-k₁（u₂-u₁）=0

节点2：k₁（u₂-u₁）-k₂（u₃-u₂）=0

节点3：k₂（u₃-u₂）-k₃（u₄-u₃）=0 （2-9）

节点4：k₃（u₄-u₃）-k₄（u₅-u₄）=0

节点5：k₄（u₅-u₄）-P=0

图2-4 节点受力图

把反作用力R₁和外力P从内力中分离出来，重建方程组（2-9），得

将以上方程组表示成为矩阵形式，有

在带载矩阵中，将反作用力和外加的持载区分开便于求解。因此，与矩阵有关的方程组（2-11）可以写为：

从式（2-12）可以很容易地看出，在节点载荷和其他边界条件下，方程组（2-11）给出的关系可以写成如下一般的形式：

R=ku-F （2-13）

即

[反作用力矩阵]=[刚度矩阵][位移矩阵]-[荷载矩阵]

在此，读者要注意外部施加的荷载矩阵F和反作用力矩阵R的区别。

在本例中，由于杆的上端是固定的，节点1的位移是零。因此，只有4个未知的节点位移u₂、u₃、u4和u₅。节点1的反作用力R₁也是未知的——总共有5个未知量。由于方程组（2-12）已给出了5个平衡方程式，因此能求出所有的未知数。不过需要注意的是，即使方程的数目和未知数的数目一致，系统方程也包含了两种不同类型的未知数——位移和反作用力。为了在求解时不同时考虑未知的反作用力和位移，而集中考虑未知的位移，可利用已知的边界条件取代系统方程组（2-12）的第一行，使u₁=0。应用边界条件u₁=0消除系统方程中未知的反作用力，使得到只有未知位移的方程，则有：

图2-5 任意单元中的内力

求解矩阵方程（2-14）就可以得到节点的位移。从以上的解释和对方程组（2-14）的观察，很清楚地知道，关于固体力学问题，只要在有限元公式中应用边界条件，就可以把给定的系统方程组（2-12）转变成一个一般的方程组形式（2-14）。这个由刚度矩阵、位移矩阵和荷载矩阵组成的一般形式，即

[刚度矩阵][位移矩阵]=[荷载矩阵]

通过上面的关系式求出节点位移后，就可以用方程组（2-13）求得反作用力。接下来，我们将建立单元刚度矩阵，并讨论总刚度矩阵的构成。

由于本例中每个单元有两个节点，每个节点有一个位移量，因而对每个单元需要建立两个方程。这些方程必然涉及节点的位移和单元的刚度。如图2-5所示，假设有单元的内力f_i和f_i+1，以及端节点的位移u_i和u_i+1。静力平衡条件要求f_i和f_i+1的和为零。注意，不管采用图中的哪种受力图，f_i和f_i+1的总和为零。不过，为保证以后讨论的连续性，这里采用图2-5b中给出的表示方法，即f_i和f_i+1的正方向相同。节点i和i+1上的载荷如式（12-15）所示。

f_i=k_eq（u_i-u_i+1）f_i+1=k_eq（u_i+1-u_i） （2-15）

将方程组（2-15）表示成矩阵形式，有

单元组装：将方程（2-16）描述的单元刚度方程应用到所有单元，并将它们组合起来（即放到一起）将得到总刚度矩阵。(www.xing528.com)

单元（1）的刚度矩阵为

单元（1）在总刚度矩阵中的位置如下：

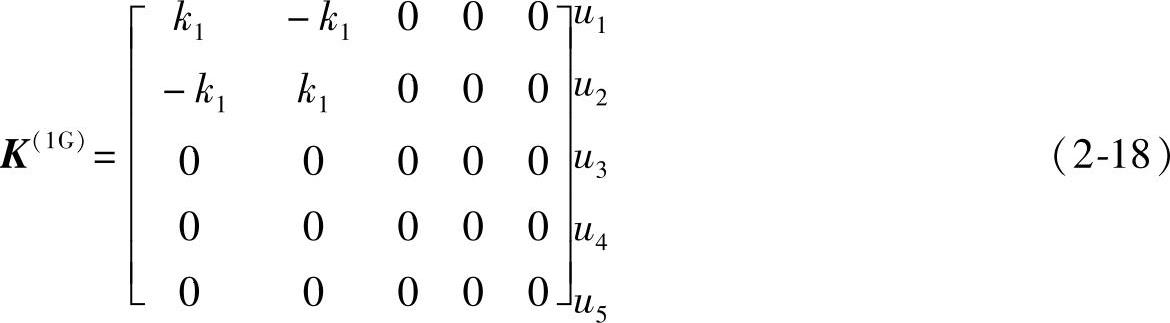
将节点位移矩阵放在总刚度矩阵中单元（1）的旁边，有助于观察节点对它的邻接单元的影响。类似地，对于单元（2）、单元（3）和单元（4），有

它在总刚度矩阵中的位置为

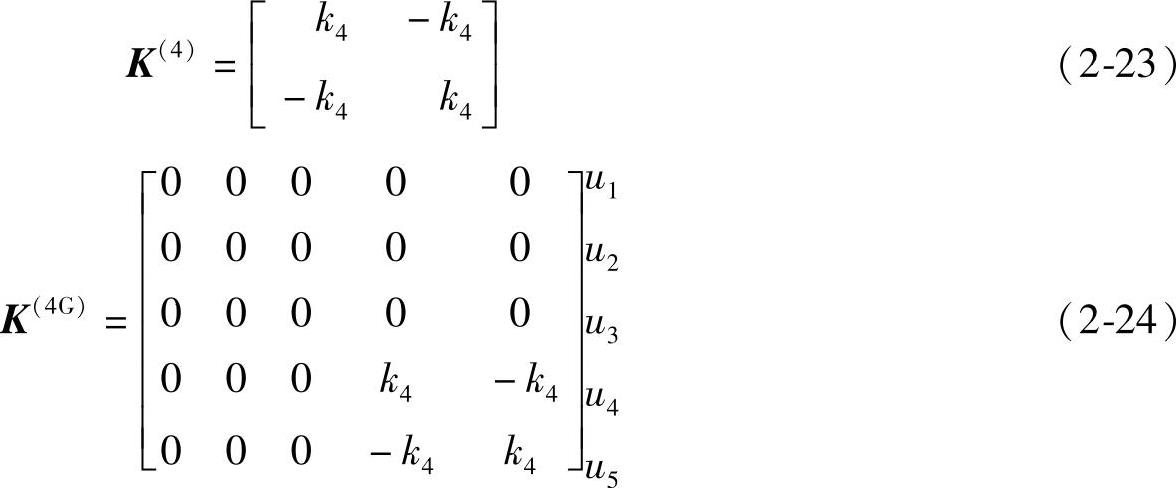
根据每个单元在总刚度矩阵中的位置将它们组合起来，即相加，就可以得到它们的最终总刚度矩阵。

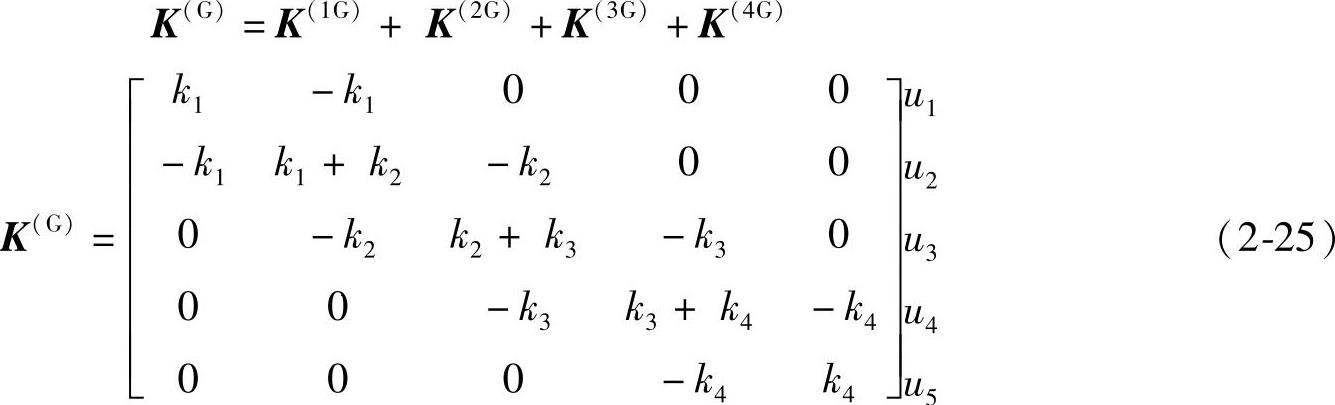
注意，由单元分析得到的总刚度矩阵如式（2-25）所示，与前面从分析所得到的总刚度矩阵，即方程（2-11）的左侧矩阵完全相同。

（4）应用边界条件和施加荷载

杆的顶端是固定的，即满足边界条件u₁=0；在节点5处作用有外力P。应用这些条件会导出线性方程组（2-26）。

注意，方程（2-26）中矩阵的第一行必须含一个1，其后跟4个0，以满足给定的边界条件u₁=0。如前所述，还要注意在固体力学问题中，有限元公式通常具有如下的一般形式：

[刚度矩阵][位移矩阵]=[荷载矩阵]

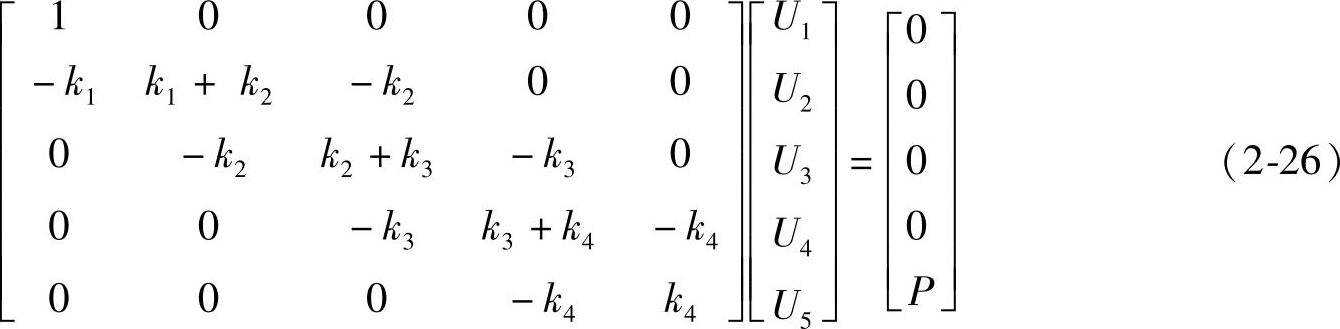
2.求解阶段

接下来联立求解代数方程组。为了得到节点的位移量，在此假定E=200GPa，w₁=0.002m，w₂=0.001m，t=0.00125m，L=0.10m，P=1000N。

杆在y方向横截面面积的变化可表示为：

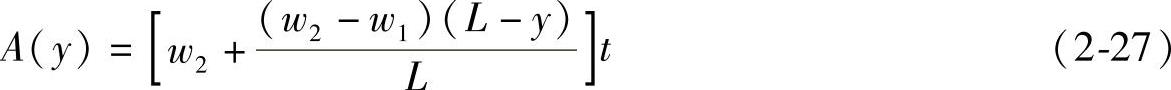
将上述参数输入Matlab，根据方程（2-27）可计算出每个节点处的横截面面积。输入Mat_- lab中的源代码如下：

输出结果如下：

单元的平均横截面积采用下式进行计算：

式中，j为单元编号，j=1，2，3，4；i为节点编号，i=1，2，3，4，5。

每个单元的等效刚度系数可由下式算出：

将上述公式输入Matlab，源代码如下：

输出结果如下：

单元刚度矩阵为：

按照式（2-25），将单元矩阵组合到一起所产生总刚度矩阵，Matlab源代码如下：

输出结果如下：

应用边界条件u₁=0和荷载P=1000N，按照式（2-26），生成求解用总体刚度矩阵、荷条件P，并求解，Matlab源代码如下：

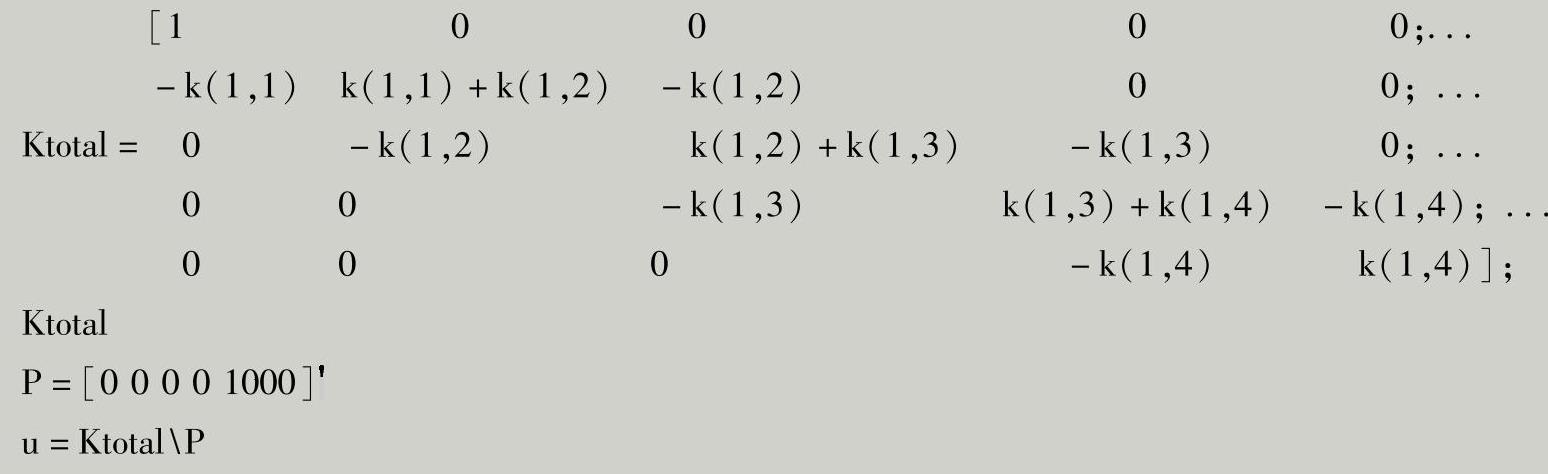
输出结果如下：

u是各节点最终的位移。

3.后处理阶段

在本例中，我们可能对其他信息，如每个单元的平均应力等感兴趣。这些值可以由如下方程确定：

由于不同节点的位移已知，还可以直接从应力和应变的关系中得到应力：

按照上述公式，输入Matlab源代码如下：

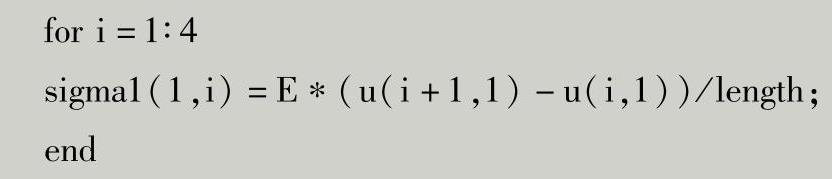
得到不同单元的平均应力如下：

注意到对于给定的问题，无论在何处将杆截断，截面的内力f均是1000N。

按照上述公式，输入Matlab源代码如下：

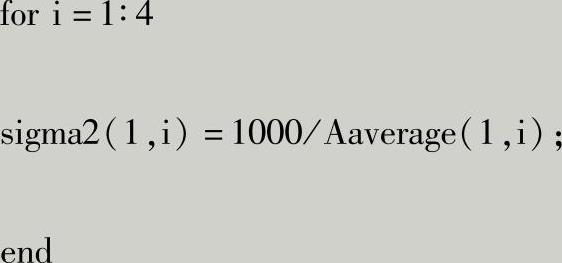
得到不同单元的平均应力如下：

我们发现这些结果和从位移信息计算的单元应力是完全相同的。经比较，就本问题而言，位移和应力的计算是正确的。上述Matlab源代码可在随书光盘中找到，以供有兴趣的读者调试使用。