地下水数值模拟基础：敏感度分析及其重要作用

1.敏感度(灵敏度)

敏感度分析(灵敏度分析)的目的是为了对已经识别过的模型的不确定性进行量化。模型的不确定性是由于在判断该模型的含水层参数、外部影响以及边界条件方面存在着不确定性所造成的。事实上,对如岩性、构造等其他方面的判断上也都存在着不确定性。所以敏感度分析应该是所有模拟结果用于实际问题时需要做的一个基本步骤。模拟结果中能为我们所接受的参数值范围也都是在模型识别和敏感度分析的基础上最终确定下来的。敏感度分析时,经过识别得到的渗透系数、贮水系数、补给量和边界条件的值都要在预先设定的、合理的范围内系统地加以改变,以观察它们的影响。一般把水头变化的大小(以识别阶段的解为基准)作为解对特定参数灵敏度的衡量标准。敏感度分析的典型做法是同一时间内只改变一个参数值,以观察它的影响。但这也并不是绝对的,同时改变两个或更多参数值有时也是可以的,它的效果可以用来考核决定合理解的最大范围是否合适。如渗透系数和补给速率可以一起改变,为此常把低渗透系数和高补给速率在一起,高渗透系数和低补给速率组合在一起加以改变,以观测它们的影响。敏感度分析也可以用来测试参数值的改变对水头以外别的因素的影响。采用自动识别程序时,也要进行敏感度分析。更有效的敏感度分析是计算敏感度(敏感度系数)。敏感度是这样定义的,它表示一个因素变化对别的因素的影响程度,通常用下式表示

式中:βi,k为模型变量(如水头、浓度等)H对第k个参数在第i个观测点上的敏感度。

如模型变量为水头,则H i表示i点的水头,a k为第k个参数值。由于不同模型变量的量纲不同,不同参数的量纲差别也很大,所以上述敏感度没有一个统一的单位和量纲。为了便于不同参数间敏感度的比较,式(5-1)也可以化为下列形式

这样敏感度的量纲就和模型变量如水头或浓度等的量纲一致了。式(5-2)还可进一步化为下列无量纲形式

这种无量纲形式更有利于不同参数、不同变量以及不同模型之间敏感度的比较。当然也可用别的无量纲形式来表示(Wagner和Gorelick,1986,1987;Hill,1998)。

βi,k值大意味着参数值改变对模型变量(如计算水头)的影响大。所以敏感度分析在参数识别中有着重要作用,往往要求在每个观测点上对每个评估的参数求它的敏感度。另外通过绘制敏感度图可以反映出模型的哪些区域对所给出的参数值的改变最为敏感。考虑到国内这方面的成果还很少,只能参考国外一些著作(如Zheng和Bennett,2002)予以简单介绍。

具体计算时,对于某一特定参数的敏感度可以采用下列近似公式加以计算:

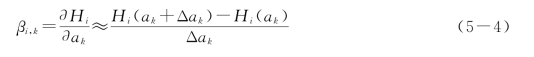
或采用下列标准化的形式

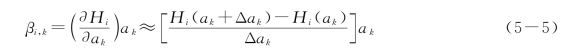
式中:a k为某实例的参数值;Δa k为参数的细小改变;H(a k)、H(a k+Δa k)分别为该实例中由该参数值所得的模型变量值和参数值有细小变化时所得的模型变量值。

显然应用式(5-4)或式(5-5)计算敏感度,需要进行一次基本实例模拟和M次附加的,每次只改变一个参数的模拟。虽然做起来简单,但当参数量多、观测点的量也多,都需要计算它们的敏感度时,这样一个计算过程从计算角度来说就显得重复、乏味、缺乏效率了。为此不少研究者对如何设法减少计算敏感度所需的计算量进行了研究,对这方面感兴趣的读者可以参考Sykes等(1985)、Wilson和Metcalfe(1985)、Schmidtke等(1987)提出的方法,限于篇幅,本书就不一一介绍了。(www.xing528.com)

式(5-4)和式(5-5)给出的敏感度只是在一个特定位置上对一个给定的参数,模型所反应的敏感度的大小。显然目标函数平方和对某一个模型输入参数的敏感度常常是很有用的,因为它定义了一个单一的敏感度,不会由于模型变量不同而有不同的敏感度。为此,人们往往以目标函数的平方和来代替敏感度公式中的模型变量,有

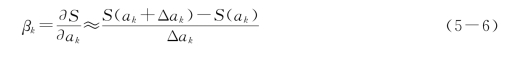
或标准化形式

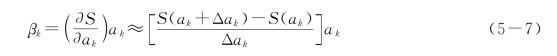
式中:ΔS为由于参数a k改变,目标函数平方和从S(a k)变为S(a k+Δa k)所引起的改变。为了对一个选定的参数a k计算目标函数平方和的敏感度,要选定一组模型参数作为基本参数,由各个观测点水头、浓度或流量的观测值和计算值来计算目标函数的平方和S值。接着保持其余参数不变,仅参数a k变化一个量Δa k,计算在这组新参数情况下的S值,于是敏感度就可用式(5-6)和式(5-7)计算了。正的βk值表明随着a k的增加,S也增加;负的βk值表明随着a k的增加,S反而减少。βk的绝对值表示野外观测值和模型模拟值之间拟合情况对模型参数a k的相对敏感度。

需要注意,如果模型变量和参数a k是线性关系,则a k的增加或减少不同的量将得到相同的βk值。若两者的关系是非线性的,a k的增加或减少不同的量就会得到不同的βk值。因此,如果模型变量和参数是非线性关系,就要详细说明参数的变化范围。从理论上讲,由有限差分近似式(5-4)～式(5-7)算出的敏感度当参数改变的大小减少时它会趋近于精确的敏感度(Zheng和Bennett,2002)。可是如Poeter和Hill(1998)指出的那样,参数变动太小会造成模型变量计算值的差别微不足道或者四舍五入的误差就使这种差别显得黯然失色了。反过来,太大的变动也会使敏感度不精确。因此,根据经验这种变动的大小以取能改变1%～5%(Zheng和Bennett,2002)为好。

2.敏感度分析

敏感度分析对下列情况非常有用:①用来考核改变模型输入参数对模拟结果的整体反应;②用来考核由于模型输入参数的不确定性可能会给模拟结果带来什么样的不确定性;③用来考核通过模型识别得到的参数满意程度如何。Zheng等(2002)主张最好在识别前后都进行敏感度分析。在识别前对系统进行少量敏感度分析,是为了总地了解模型对一些参数的反应。这样的运算有助于消除某些难以发现的错误或模型建立中不协调的地方。接着在识别得到一组最优参数后,进行敏感度分析是为了确定模型的结果对模型参数的敏感程度。它将提供有关模型参数如何影响模拟结果不确定性的重要信息。如果模拟结果对某一特定参数高度敏感,那么模型做出重要解释和预报的能力将受到和该参数有关的不确定性的严重影响。换言之,如果模拟结果对某一给定参数不敏感,就意味着该参数领域的不确定性对模型解释和预报能力的影响就非常有限了。

敏感度分析可以作为确定对计算结果影响最大的模型输入参数不确定性的手段,为我们提供了一种识别模型输出中不确定性主要贡献的手段。敏感性分析方法通常可以分为两类:局部敏感性分析法和全局敏感性分析法。局部敏感性分析法每次只能评价单个变量的变化对系统输出的影响;而全局敏感性分析可以在检验单个变量变化对系统输出影响的同时分析变量之间的交叉作用对系统输出的影响。在局部敏感度分析中,首先需要做基本实例模拟,它是用通过最有效估计所得模型输入参数进行的。以后每次模拟都是从这个基本实例模拟中用的参数值出发,只改变其中某一个模型参数的值以某个百分比,其他参数保持不变。把每次模拟结果和基本实例模拟的结果相比较,计算被改变的那个参数的敏感度。模拟结果和基本实例模拟结果相差愈大,表明计算的敏感度就愈大。换句话说,一个给定的输入参数的不确定性对整个模型结果不确定性的贡献随着该参数敏感度的增加而增加。所以敏感度是一个输入参数不确定性对整个计算结果不确定性贡献的定量指标。

在不确定性评估中采用敏感度分析的主要优点是简单、灵活。它能够通过简单的多次模拟运算来实现,不需要模拟者对地质统计学或随机过程有广博的背景。能用它来分析由输入参数如渗透系数等引起的不确定性,并且能方便地加以量化,但这种方法对有些问题如不同地质单元间的边界就不好定量估计它的位置了。

敏感度分析应用于不确定性评估,蕴藏着一个问题,那就是输入参数间的相互关系。敏感度分析中,包括全局敏感性分析,各参数都假设是相互无关的,每个参数是独立变化的。然而实际上,参数常常在一定程度上是相互关联的,忽略这些相互关联可能会导致敏感度分析结果出现某些问题。例如,对渗透系数变化所引起的模型反应的敏感度是在补给速率保持不变,假设这两个变量是彼此独立的情况下计算得来的。实际上,渗透系数和补给速率常常有很强的相互关系,渗透系数大的地区,补给速率常常比较大,反之亦然。所以计算的渗透系数敏感度可能并不能精确反映模拟结果对该参数的敏感度。应用敏感度分析于不确定性评估的另一个问题是非线性问题。模型的预报通常是输入参数的非线性函数,而应用敏感度就意味着是线性关系,这是应用敏感度分析来做不确定性评估的另一个问题。这么一来,敏感度分析的结果就受选择何种基本实例来模拟和每个输入参数变化的百分比有多少的影响。

最后应指出敏感度分析是评估不确定性的一种确定性方法。它并没有考虑输入参数的概率结构,也不能定量表示任何给出结果的概率。尽管有这些不足,敏感度分析仍然是一种快速、近似分析模型不确定性的实用和有力工具,也可以看作是更进一步的以概率或随机方法为基础的不确定性分析的先驱(Zheng和Bennett,2002)。

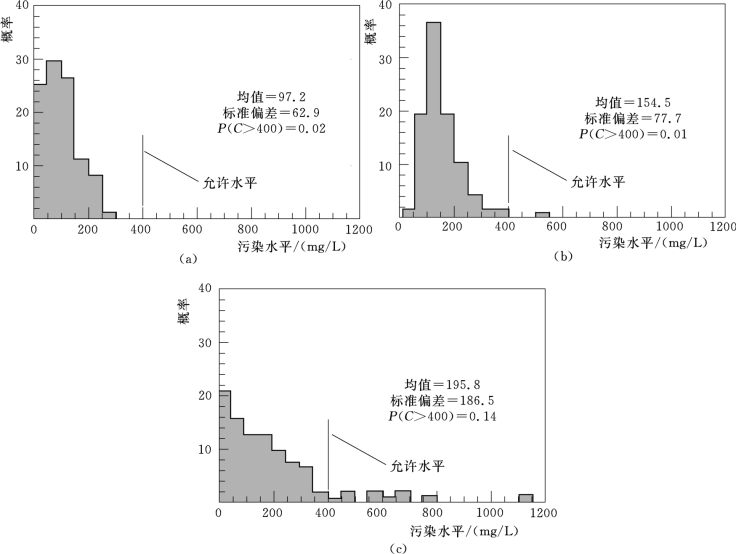
图5-1　污染水平的概率分布

(a)渗透系数作为随机变量;(b)初始污染羽的形状作为随机变量;(c)渗透系数和初始污染羽的形状都作为随机变量
(据Woldt等,1992修改)