地下水数值模拟：有限元方程及基本特性

仍以三角形单元为例。由于式(3-14)中基函数的性质,ψi只在以i为公共点的几个三角形组成的多边形(以Ωi表示,设共有m个单元)上不为零。所以式(3-14)中的累加事实上只要对Ωi上m个单元累加就可以了。且在以i、j、k为顶点的单元e上,只有ψi、ψj、ψk不为零,其他结点的基函数在e上均为零,故e上的函数近似表达式可直接写成

式中:H i、H j、H k为结点i、j、k上的水头值。

由式(3-22)、式(3-24)可得

如i点位于第二类边界Γ2上(图5-4),则ψi在abjk上为零。式(3-14)中的

如单宽流量q在ai和ik上分别为q ai和q ik,则

ψi沿ik和ai上是线性变化的,由此不难求得在ik上,该函数为(薛禹群和谢春红,1980)

式中:s为从i点算起的长度;L ik为线段ik的长度。

于是

同理可得ai段上的线性积分值。于是有

式中:L ai为线段ai的长度。

所以对结点i而言,这一部分水量相当于i点两侧各一半单元边长的侧向补给量。Γ2上的其他结点也按此方法计算。若i点为第一、第二类边界的交界点,如ai段为第一类边界,a点水头已知,ik位于Γ2上,则此项值为。

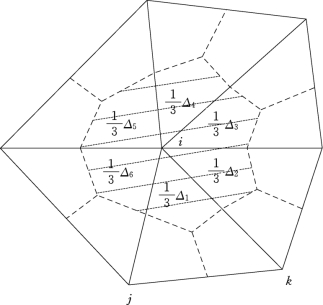
图3-5　源汇项的计算域

式(3-14)中有关源汇项的积分,利用积分公式(薛禹群和谢春红,1980):

有

式中:w e为该单元上w的平均值。故对结点i来说,源汇项相当于图3-5中阴影部分的垂向交换水量。

把它们一起代入式(3-14),对于第二类边界上的结点可得

利用积分公式(薛禹群和谢春红,1980)

式(3-26)可以化为

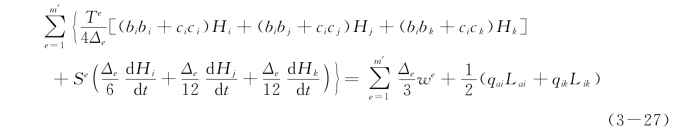
式中:T e、Se、Δe分别为单元e上导水系数、贮水系数的平均值和单元e面积。

如结点i是内结点,ψi在周界上为零,故

即式(3-24)中最后一项应为零。

用同样的方法列出其他内结点和第二类边界结点的方程。n个这样的结点,一共可以得到n个含n个未知数的一阶常微分方程。如

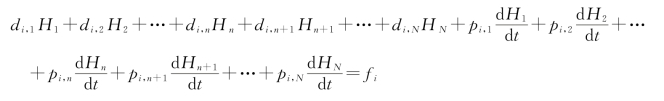
由于第一类边界Γ1上结点的水头及其对时间的导数是已知的,式(3-27)中涉及结点n+1、n+2、…、N的水头及其对时间的导数项应按式(3-15)移到等式的右端,于是可得与式(3-15)相应的方程为

(www.xing528.com)

其中

这是对各向同性介质而言的,如果是各向异性介质,则有

如果坐标轴选得和渗透系数张量的主方向平行,则

而

其中矩阵[D]、[P]和矢量{F}的元素分别为

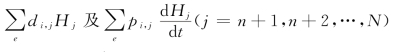其中[D]{H'}和由组成。

式(3-28)即式(3-15)。把其中的化为差分形式,即得式(3-16)或式(3-17)。求解此方程组即得各结点的水头值。

如果某单元e上还有越流项,也可作类似处理,在有关结点的式(3-13)的左端加上

于是式(3-15)将改为

式中组成矩阵[G]和矢量{F}的元素为

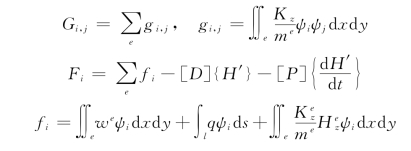
式中:、me、分别为越流所通过的弱透水层的垂向渗透系数、厚度和补给层水头在该单元上的平均值。

如采用线性三角形单元,则只要在有关结点的式(3-27)中,在方程的左端加上

此时式(3-29)中的有关元素为

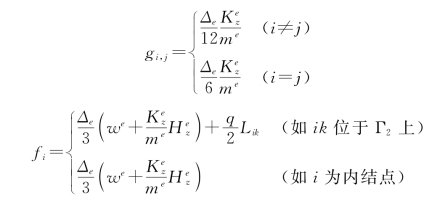
最终形成的式(3-16b)中的渗透矩阵[A]为

[A]=[[D]Δt+[G]Δt+[P]]

如果结点i上还有流量为Q i的抽水井,井心位于结点,则应在式(3-14)的右端加上一项

井径r w通常很小,基函数在井周界Γw上的值可视为它在i点上的值ψi,此时ψi=1。于是

意味着只要在相应结点的方程的右端减去一个井流量Qi。Ω内其他的井,由于ψi的性质,它对i点没有影响。没有井的结点,此项为零。如为注水井则加上一个井流量。如抽(注)水井位于单元内部,井心坐标为(x w,y w),流量Q(注水井Q＜0),则把它看成是井管面积F w上,单位时间、单位面积上的垂向流出(入)含水层的水量w=-,在单元的其他地段则为零。于是对单元e上的结点i、j、k依次有

由于ψi+ψj+ψk=1,抽(注)水井流量在上式中按三个结点的基函数值作为权分配到各个结点上,其和恰等于井流量。只要i、j、k点都不在Γ1上,就应在相应结点方程的右端减去(注水井为加)分配所得的上述这部分流量。如抽水井位于形心,则各结点分别分配到Q/3。

最后应指出,有限元法不论Rayleigh-Ritz法还是Galer kin法,它们的最终结果式(3-28)还是一致的;其次,两种方法一般都是从整体质量守恒出发。如Galer kin法来源于加权剩余使整体(整个渗流区Ω)的误差最小。整体质量守恒了,但对Ω内某一个小区来说不一定都能保证质量守恒。局部可能质量不守恒是有限元法的主要缺陷。由此,有时可能引起模拟非稳定流预报地下水位时在开始阶段水位变化出现异常。即抽水时有些结点的模拟水位有时反而会上升。Neu man等(1976)指出把贮水矩阵改为对角阵时,上述反常现象会得到很大改善。此时需要把某结点i的水头变化近似地看作在Ωi中的平均值,即用i点的水位变化来近似地代表在Ωi中的变化。如e为Ωi中的一个任意单元,则有

同时,式(3-27)也要相应地改为

在最终形成的常微分方程组={F}中,矩阵[P]的元素为

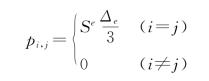
此时[P]就成了对角阵,[D]和{F}的元素则不变。