地下水数值模拟基础：Galerkin法及稳定性选择

Galer kin法是加权剩余法的一个特例。故先从加权剩余法说起。设有一微分方程

边界条件为

式中:u为x、y和z的函数;L、F表示对u进行某种微分运算;Γ为渗流区Ω的边界。

用下列形式的试探函数作为式(3-1)的近似解,即

式中:ψj为在整个域上定义、线性独立、且满足边界条件式(3-2)的函数族,这些函数称为基函数或形函数和插值函数;N为结点总数;αj为待定系数。

由于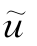只是一个近似值,把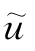代入式(3-1)后,一般会有误差或剩余ε存在。

加权剩余法就是选择待定系数αj使得误差在某种意义上成为最小。显然,令ε的积分为零。

的方案最简单。但对N个未知数来说目前还只有一个方程,无法求解。为此引入互相线性独立的权函数ωi,i=1,2,…,N,对上式进行修正,这样便可以得到N个方程

求解这些方程便可确定N个未知数α1、α2、…、αN。把它们代入式(3-3)后就得到式(3-1)的近似解。

因选择权函数的方法不同,有多种加权剩余法,常用的是Galer kin法。Galer kin法选择基函数ψi作为权函数,即ωi=ψi,有

以下述定解问题为例来说明Galer kin有限单元法:

式中:H 0为水头初值;φ1为第一类边界Γ1上的已知函数;q为第二类边界Γ2上的单位宽度侧向补给量;n为边界Γ2的外法线方向;其余符号意义同前。

设近似解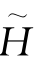用下列试探函数

表示。把它代入式(3-5),即在式(3-6)两端乘以基函数ψi,积分并移项得

式中:n为除了第一类边界上的结点以外的结点总数,即未知结点的总数。

应用分部积分法于上式得

上式左端第一项应用Green公式有:

式中:Γ为Ω的周界;n为Γ的外法线方向。

由于第一类边界Γ1的水头已给定,所以上述沿边界Γ的积分项事实上只存在于第二类边界Γ2上。于是整个方程(适用于Γ2上的结点,对于不在第二类边界上的其他结点,最后一项为零)可改写为(www.xing528.com)

式(3-12)为Galer kin方程的一种形式。

由式(3-10)得

把它们和边界条件一起代入式(3-12),同时考虑到即使在各向异性介质,T也是对称张量,所以可以改写为。于是有

ψi在不同的单元上有不同的表达式,所以上述积分必须按单元逐个计算后再求和,即

式中:m为单元数;n e为单元结点数;l为位于Γ2上单元e的线元,即Γ2∩e。

对于不在Γ2上单元,此项为零。由于结点n+1、n+2、…、N在Γ1上,它的水头及其对时间的导数是已知的,把它们移到方程右端与已知项合并。于是式(3-14)可用矩阵表示为

其中导水矩阵[D]、贮水矩阵[P]、矢量{F}分别为

其中[d]、[p]、{f}为典型单元的单元矩阵和矢量,其元素分别为

式中:{H}、分别为由H 1、H 2、…、H n和组成的列矢量;{H'}、分别为由Γ1上已知水头和水头对时间导数已知的H n+1、H n+2、…、H N和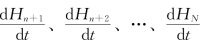组成的列矢量。

式(3-15)代表一个常微分方程组。对式中取差商;对各点水头有多种取法:显式方法取t=κΔt时刻的水头Hκ;隐式方法取t=(κ+1)Δt时刻的值Hκ+1;中心式差分方法取t=时刻的水头。显式方法的稳定是有条件的,Δt取值受限制。隐式方法和中心式差分方法则是无条件稳定,Δt取值不受限制的优越性。所以一般多采用隐式方法。此时式(3-15)化为

或

其中渗透矩阵

[A]=[[D]Δt+[P]]

{B}=[P]{Hκ}+{F}Δt

如采用中心差分法,则式(3-15)化为

除了上述几种处理时间导数的方法外,还有类似有限差分法那样,通过权函数把显式和隐式结合在一起的,但只有权函数θ≥0.5才能无条件稳定。

给出初值Hκ后,求解线性代数式(3-16)或式(3-17),可以求出第一个时段终了时刻的水头Hκ+1。再把此Hκ+1作为初值,重复上述过程可以依次求出各个时刻、各结点的水头值。