地下水数值模拟基础：解决二维地下水流问题的差分方程

以下列方程

为例加以说明。边界条件采用第一类边界条件,渗流区Ω边界上的水头是已知的,初始水头也是已知的。采用平行于坐标轴的直线x=iΔx、y=jΔy把Ω分割为网格区(i=0,1,…,l;j=0,1,…,l)。时间分割为t=κΔt(κ=0,1,…,m)。某结点的水头记为Hκi,j=H(iΔx,jΔy,κΔt)。为简化表达式采用下列符号:

故式(2-16)在结点(i,j)有显式差分格式

其收敛和稳定必须满足的条件是

相应的隐式差分格式为

或当Δx=Δy时,有

其中

式(2-19)和式(2-20)是无条件收敛和稳定的,Δt取值不受Δx、Δy的严格限制。与式(2-16)相应的中心式差分格式为

它也是无条件收敛和稳定的。以上几种格式的截断误差和一维问题相同。

如前所述,上述几种差分格式可以统一到下列加权显式-隐式格式中

权因子θ=0时即为显式方法;θ=1时,即为隐式方法;θ=1/2为中心式差分格式。

显式方法Δt取值受严格限制,所以在实际工作中用得很少。隐式方法和中心式差分方法的方程中都含有5个未知数,需要对所有内结点都列出相应的方程式(2-19)或式(2-21),利用边界条件形成方程组,联立求解。但占用内存大,求解也比较困难。为了便于求解,Peaceman和Rachf or d(1955)提出了交替方向隐式差分法,简称ADI法(Peaceman-Rachf or d格式)。ADI法是目前求解地下水流差分方程最好的方法之一。

此法的特点是在tκ和tκ+Δt之间设想有一个过渡的中间时刻tκ+Δt/2。计算分两步进行。从tκ到tκ+Δt/2,式(2-16)中对x方向取隐式差分,y方向取显式差分,即(www.xing528.com)

或当Δx=Δy,时,有

求出过渡时刻的水头(中间解)hκ+1/2i,j　(此中间解没有任何实际物理意义)后,再对x方向取显式差分,y方向取隐式差分,有

或当Δx=Δy时,有

由此求得该时段终了时刻tκ+Δt=(κ+1)Δt的水头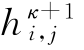。此处不难看出,从一个时刻到下一个时刻,每推进一个时间水平,需要解式(2-23)、式(2-25)各一次,在x、y方向交替使用隐式差分,故称为交替方向隐式差分法。

具体应用时,分两步进行:

(1)利用式(2-23)计算过渡时刻的水头分布。为此先要根据边界的性质是第一类边界或第二类边界分别进行编号。以结点法为例,若下边界是第一类边界,则取j=1(若该行为第二类边界则取j=0,1)。如该行左端为第一类边界时,取i=1(若为第二类边界时,取i为0,1,2,3,…,l-1(当右端边界l列为第一类边界时。若为第二类边界,则取至i=l)形成l-1个(或l+1个)方程,含l-1(或l+1个)未知水头、、…、(该行两端边界均为第二类边界,则有l+1个未知水头…、)。这是一个三对角线方程组,很容易求解。接着依次取j=2(或1,2),3,…,l-1(或l,当上边界第l行为二类边界时),重复上述运算,即可求出κ+1/2时刻所有内结点的水头值。

(2)利用式(2-25)计算κ+1时刻的水头值。计算步骤与(1)相似,只是由逐行进行改为逐列进行。

式(2-23)和式(2-25)单独应用时,每个方程都只是有条件稳定。但结合起来构成上述两步计算法时,对于λ＜∞,却是无条件稳定的(Lapidus和Pinder,1982)。所以Peaceman-Rachf or d的ADI法是无条件稳定的。但必须指出,在三维情况下,就不是无条件稳定的了。式(2-23)和式(2-25)只含有三个未知数,形成的是三对角线方程组。它可以用下面将要提到的追赶法快速求解,具有占用内存少,运算速度快的特点。这种方法的精度是O([Δt]2+[Δx]2+[Δy]2)。所以它是求解地下水问题的一种非常有效、非常快速的方法。当渗流区形状接近一个矩形时,效果更好。

如果水流方程中有源汇项,如

则Peaceman-Rachf or d分裂格式有下列形式

此时,Δx=Δy,。