地下水数值模拟基础：显式差分格式

为了便于说明,以下列一维河间地块均质各向同性承压含水层中的地下水流问题

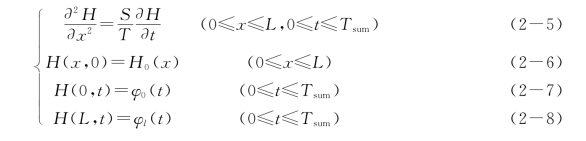
为例来加以说明。

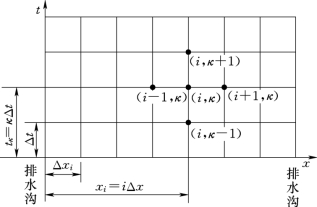
图2-1　研究区域网格示意图

首先将研究区域[0,L]用直线等分为l份,步长Δx=L/l,把时间段[0,T sum]用直线等分　成m份,时间　步　长Δt=T sum/m,构成如图2-1所示的网格,结点坐标x i=iΔx,tκ=κΔt(i=0,1,…,l;κ=0,1,…,m),简　记　为(i,κ),并　以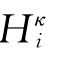表　示H(iΔx,κΔt),以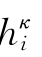表示原方程的差分方程解(即H的近似值)。

式(2-5)中的导数,用差商代替,在典型结点(i,κ)处表示为

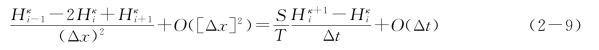
略去O(Δt)和O([Δx]2),可得和式(2-5)以及图2-1中x,t平面上的网格对应的差分方程为

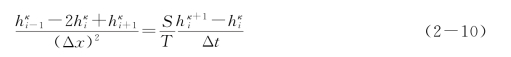
截断误差为O(Δt)+O([Δx]2)。即当Δt和Δx很小时,这一误差是Δt阶的一个量与(Δx)2阶的一个量之和。若定义(www.xing528.com)

则式(2-10)可改写为

由此可知,只要知道某一时段κ开始时刻tκ各结点的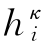值,利用上式便能算出tκ+1时刻,即κ时段终了时刻的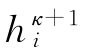值(1≤i≤l-1,1≤κ≤m)。所以称这一方法为显式方法。边界结点的水头值则由边界条件给出,即

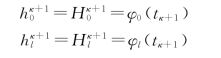
这样利用t=0时刻时各结点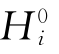的值已由初始条件式(2-6)

给出的情况,直接计算t 1时刻各内部结点的水头值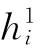,并利用边界条件补充边界结点上的水头值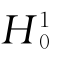、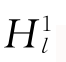。再把求得的t 1时刻各结点的水头作为初值,重复上述过程求t 2时刻各结点的水头值。如此一个时间水平、一个时间水平地做下去,就能求得计算区Ω上所有时刻的水头值。

前面我们给出了求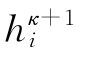的方法,但必须回答一个问题,即差分方程的解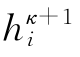是不是很逼近原微分方程的解在相应结点上的值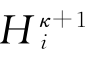?为此,需要从两个方面,即差分方程的收敛性和稳定性来回答上述问题。

如果差分方程的解在步长Δx、Δt取得充分小时,和微分方程的解析解在某种意义上很接近的话,便说这种差分格式是收敛的。研究收敛性就是讨论当Δx→0、Δt→0时,差分方程的解和微分方程解的差(在一维条件下为)的绝对值在什么条件下趋近于零。其次,实际计算中由于只能用有限位计算,每一步都会有舍入误差,而且它还影响以后的计算结果。于是要考虑一个问题,当某一步结果本身有误差时,利用它去计算,若Δx和Δt固定,随着计算时间或计算次数的增加,误差是逐渐消除?还是逐步积累,愈变愈大?如是后者,则当t→∞时(或计算次数无限增多时),尽管某一步的误差很小,但其影响最终有可能达到十分可观的程度,使所得解面目全非。这时所考虑的差分格式便是不稳定的。显然,不收敛和不稳定的差分格式是没有实用价值的。

显式格式经证明,只有当0＜λ≤1/2时才收敛和稳定。因此,Δt不能取的太大。