总共研究了在跨中施加集中荷载的6根简支梁,典型的横截面如图9.17所示。梁B1,B2,B3和B4在单调荷载下进行测试,其中B1和B2由作者测试,B3和B4取自Burns和Siess(1966)的Beam J-1和Beam J-10。对于经历循环加载的梁B5和B6的结果分别取自Burns和Siess(1966)的Beam J-11和Park等人(1972)的Beam 24。由于对称性,可以仅使用半梁结构的规则网格进行分析。
高屈服变形钢筋和低碳钢圆钢分别用符号“T”和“R”表示,直径的单位为“mm”。6根梁的主要特性如表9.1和表9.2所示。L表示简支梁的总长度,L0表示简支梁的净跨度,bw和h是矩形截面的宽度和高度,fco,ft和Ec分别是混凝土的抗压强度、抗拉强度和初始模量,fy是拉伸钢筋的屈服应力。6根梁的初始泊松比均取为0.15。

图9.17 矩形梁的典型截面
表9.1 试验简支梁的结构尺寸 (单位:mm)

表9.2 试验梁的材料属性

6根梁的数值模拟中局部黏结应力-滑移关系的假设参数如表9.3所示。由于黏结参数具有较大的离散性,已经尝试用正常范围内的各种值来模拟裂缝图形,该裂缝图形对黏结参数特别敏感。残余黏结应力取自CEB-FIP Model Code 1990(1993),即τr=0.15τu。滑移值S1,S2和S3的选择主要采用Mirza和Houde(1979)推荐的值,并且6根梁都采用相同的值。
表9.3 局部黏结-滑移关系

1.在单调荷载作用下的试验梁(B1,B2,B3和B4)
梁B1,B2均设有R12箍筋,间距175 mm,屈服应力为328 MPa,弹性模量为186 GPa。在分析中,用一个30(垂直)×150(水平)的规则网格来建立半梁结构模型。跨中荷载分布在7个节点上,每个反力分布在5个节点上。这里研究的梁B3和梁B4实际上分别是Burns和Siess(1966)的Beam J-1和Beam J-10。梁中还有间距为152 mm的T10箍筋。在分析中,采用30(垂直)×198(水平)的规则网格对梁的一半进行建模。跨中荷载也同样分布在7个节点上,每个反力分布在5个节点上。
4根梁的荷载-位移关系的试验和数值模拟对比如图9.18所示,表明二者具有良好的一致性。在每种情况下,荷载-位移曲线由一个陡峭的初始部分和一个相当平坦的部分组成,陡峭的初始部分代表高的未开裂刚度,一个较小的陡峭部分与降低的开裂刚度有关,一个相当平坦的部分则代表加载中的钢筋屈服。

图9.18 单调加载下荷载-位移曲线比较
图9.19和图9.20分别显示了试验梁B1和B2的裂缝模式,阴影为拉伸开裂的混凝土。由于所使用的网格相当精细并且在有限元建模中考虑了黏结滑移,因此破坏区域形成裂缝带,这与试验中观察到的裂缝模式十分一致。根据发生的顺序,裂缝从0开始编号。在每种情况下,第一条裂缝(裂缝0)大致形成在中间跨度处,其对应梁的横断面弯矩是最大的。随着施加荷载的增加,数条裂缝(B1的裂缝1~3;B2的裂缝1和2)在梁中间1/3范围内逐渐形成。这些初级裂缝主要是由弯矩引起的。随着施加荷载的进一步增加,在先前的初级裂缝之间形成一些二次裂缝(B1的裂缝4;B2的裂缝3)。在目前的试验装置中,只有中跨处的裂缝是真正的弯曲裂缝。在中跨以外位置的裂缝基本上是弯曲剪切裂缝,由弯曲引起,但是在沿着大致垂直的路线行进之后它们逐渐变得倾斜。结果表明,该断裂模型和所开发的程序能够很好地模拟弯曲和弯曲剪切裂缝的形成。

图9.19 试验梁B1的裂缝模式(荷载105 k N)
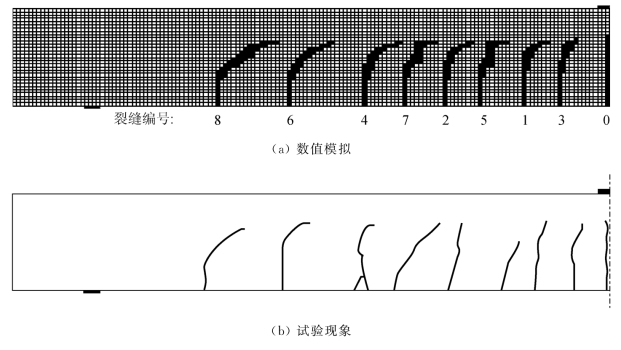
图9.20 试验梁B2的裂缝模式(荷载150 k N)
图9.21显示了试验梁B1和B2主梁中钢筋应力的变化以及裂缝顺序编号。钢筋应力的变化清楚地反映了钢筋与混凝土之间的相互作用以及黏结滑移的影响。应力变化不是遵循弯矩图的三角形形状,而是由一系列对应于裂缝位置的局部峰以及它们之间的凹陷曲线组成,这是裂缝形成和黏结滑移的特征。显然,在裂缝处,钢筋基本上承载所有张力,从而产生局部峰值,而在裂缝之间,混凝土承受部分张力,从而引起下垂曲线。根据观察,随着施加荷载的增加,钢筋和混凝土中的拉应力趋于相应增加。当混凝土拉伸应力变得过大时,在初级裂缝之间可能发生二次开裂。

图9.21 抗拉钢筋应力的纵向变化特征
图9.22显示了试验梁B1和B2抗拉钢筋的黏结应力和黏结滑移沿纵向的分布特征。注意到黏结应力和黏结滑移在裂缝处突然改变方向。在裂缝之间存在一个位置,其中黏结应力和黏结滑移均为零,并且该部分两侧的黏结应力方向相反。裂缝之间的黏结滑移光滑变化,在有些裂缝处达到局部最大值或最小值。然而,在许多情况下,裂缝处不会发生局部最大或最小黏结应力,这是因为裂缝处的黏结滑移量已经超过了与最大黏结强度相对应的黏结滑移值。

图9.22 黏结应力和滑移沿纵向的变化特征
还存在这样的情况,即裂缝间局部最大黏结应力可能小于黏结强度,即使裂缝间的黏结滑移超过了与黏结强度对应的滑移。图9.22中的例子包括梁B1的裂缝4和5之间的正黏结滑移和应力分布,梁B2的裂缝3和5之间的正黏结滑移和应力分布。这是由于新的裂纹形成时,黏结滑移和应力的重新分布造成的。例如,梁B1的裂缝1和裂缝2之间形成裂缝4之前,尚未形成的裂缝1和裂缝2之间的黏结滑移和应力大多为正。裂缝4的形成对邻近区域的影响尤为明显,导致了黏结滑移和应力的重新分布,降低了裂缝1和裂缝2之间的黏结滑移和应力。在裂纹1和裂纹2之间存在一个与黏结强度对应的黏结滑移点,但这实际上是由黏结应力滑移包络线下降支路上的一个点卸载引起的,因此黏结应力要低得多。因此,即使结构受力单调,局部黏结滑移沿钢筋仍可能发生荷载反转。进一步加载时,如果黏结滑移未超过与黏结强度相对应的滑移量,则裂缝间的黏结应力仍有可能达到黏结强度。(https://www.xing528.com)
为了进一步评估黏结强度τu和相关黏结滑移S1的变化对荷载-位移响应和裂缝模式的影响,对梁B1使用4个不同的τu值进行参数研究,对梁B2使用4个不同的S1值进行参数研究。梁B1和B2的荷载-挠度响应分别如图9.23和图9.24所示,结果表明,荷载-挠度响应对黏结参数相对不敏感。梁B1和B2的相应裂缝图案分别绘制于图9.25和图9.26,结果表明裂缝图形对黏结参数非常敏感。观察到当τu增加或S1减小时,主要裂缝间距减小。中间跨度的主要裂缝以及梁B1和B2的近支撑之间的平均间距分别列于表9.4和表9.5中。图9.27简单演示了梁B1的中性轴变化特征,由图可知,中性轴随着裂缝而波动。
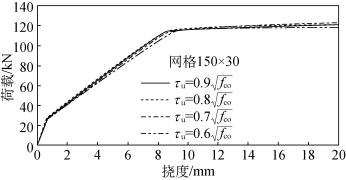
图9.23 试验梁B1荷载-位移关系曲线(S1=S2=0.03 mm,S3=0.2 mm,τr=0.15τu)

图9.24 试验梁B2荷载-位移关系曲线(S3=0.2 mm,![]() ,τr=0.15τu)
,τr=0.15τu)

图9.25 试验梁B1开裂模式(S1=S2=0.03 mm,S3=0.2 mm,τr=0.15τu,P=105 k N)

图9.26 试验梁B2开裂模式(S1=S2,S3=0.2 mm,![]() ,τr=0.15τu,P=150 k N)
,τr=0.15τu,P=150 k N)

图9.27 试验梁B1的中性轴变化特征(P=110 k N)
表9.4 试验梁B1的一级裂缝间距(S1=S2=0.03 mm,S3=0.2 mm,τr=0.15τu)

表9.5 试验梁B2的一级裂缝间距(S1=S2=0.03 mm,S3=0.2 mm,![]() ,τr=0.15τu)
,τr=0.15τu)

2.在循环加载下的试验梁(B5和B6)
这里研究的梁B5实际上是Burns和Siess(1966)的Beam J-11。梁上设有间距为152 mm的T10箍筋。使用30(垂直)×198(水平)的规则网格来对分析中的半梁结构进行建模。在试验中应用了非逆循环加载。如图9.28所示,试验和数值计算结果之间吻合理想。
这里研究的梁B6实际上是Park等人(1972)研究的Beam 24。与梁B5一样,箍筋未进行建模。在分析中使用20(垂直)×152(水平)分度的规则网格来对半结构进行建模。图9.29显示了加载行为可以得到较好的近似模拟。

图9.28 试验梁B5(网格198×30)

图9.29 试验梁B6(网格152×20)
3.网格划分的影响
为了评估网格尺寸对结果的影响,使75×15和50×15的较粗网格重新分析梁B1。结果表明,载荷-位移响应对网格尺寸不敏感,如图9.30所示。图9.31显示了不同网格方案下的计算裂缝图形,结果显示,所有网格可以合理地预测初级裂缝间距,但只有精细细网格能够预测次级裂缝。

图9.30 试验梁B1荷载-挠度关系的网格尺寸效应

图9.31 试验梁B1开裂模式的网格尺寸效应
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




