1.混凝土双轴本构模型
混凝土双轴本构模型中混凝土采用正交各向异性本构模型，采用正交主应变轴上的等效单轴应力-应变关系（Darwin，1974）。由于主应变轴的方向通常在荷载施加期间旋转，因此又称为旋转裂缝法。该模型的完整描述包括双轴强度包络线的定义以及单调和循环单轴应力-应变关系。
所采用的双轴强度包络线描述了双轴压缩区域、压缩-拉伸区域和双轴拉伸区域三种情形。为简单起见，混凝土的压缩应变和拉伸应变分别表示为正和负，也适用于应力。但是，强度值始终视为绝对值。对于双轴压缩区域，采用Vecchio（1992）提出的模型，其与Kupfer等人的试验数据能很好地吻合（1969）。两个正交方向上的主应力分别表示为σ1和σ2，并且σ1≥σ2。如图9.11（a）所示的双轴压缩区域的破坏面由下式给出：
式中，fco是单轴混凝土抗压强度；σip是沿正交各向异性i轴的抗压强度。
对于压缩-拉伸区域，采用基于剪切板试验（Vecchio，1982）结果的模型。假设压应力不影响正交方向上的拉伸强度，但拉应力将降低正交方向上的抗压强度，如下式所示：
式中，β是折减系数；εi是横向拉伸应变；εo是与单轴抗压强度相对应的应变。图9.11（b）显示了折减系数β随εi/εo的绝对值的变化。
图9.11 混凝土双轴强度包络曲线
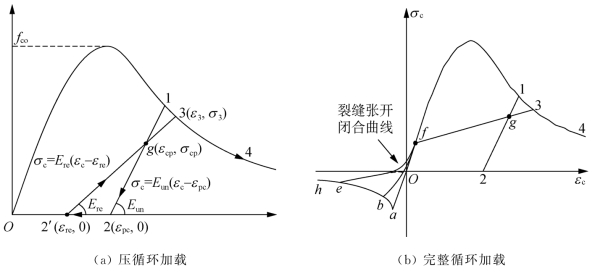
图9.12 混凝土单轴循环加载响应
由Attard和Setunge（1996）提出的完整的压应力-应变曲线，可适用于强度为20~130 MPa范围的现浇混凝土。在该模型中，用于建立应力-应变曲线的参数是初始杨氏模量Ec，峰值压缩应力fco和相应的应变εco，以及曲线下降分支上拐点处的压应力fci和应变εci。在压应力下，混凝土的应力σc与应变εc有关：
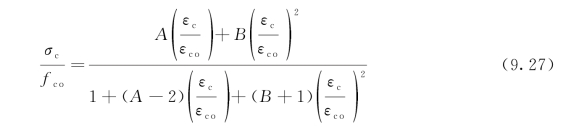
式中，A和B是取决于具体等级的系数。需要两组系数A和B，一组用于曲线的上升分支，另一组用于曲线的下降分支。
对于上升分支εc≤εco，它们取值是
对于下降分支εc>εco，它们取值为
参数Ec，εco，fci和εci理论上与fco的值有关：
考虑到拉应力下的抗裂后阻力，采用Guo和Zhang（1987）提出的模型，即：
式中，ft是抗拉强度；εt是抗拉强度对应的应变；α是与混凝土相关的参数。
对于循环响应，采用Elmorsi等人（1998）提出的模型，如图9.12所示。图9.12（a）显示了压应力下在典型路径0—1—2—2'—3—4的循环响应。在沿着包络线加载到点
之后，卸载沿着直的初始卸载区域1—2朝向点2（εpc，0），然后是零刚度区域2—2'。根据Elmorsi等人（1998）的假定，初始卸载路径1—2的斜率Eun可以根据卸载应变
和峰值压缩应力下的应变εco给出：
(www.xing528.com)
如果在初始卸载区域1—2中重新加载，则它将沿袭相同的卸载路径，直到它到达包络曲线。然而，在零应力区域中的点重新加载将遵循不同的路径，如路径2'—g—3。路径2'—3和1—2在公共点g（εcp，σcp）处相交，该公共点被假设为满足
（Elmorsi，1998），因此可以相应地计算出重新加载时的刚度Ere。在卸载和重新加载过程中，应力σc与应变εc相关：
如果循环荷载延伸到超过原点O的拉伸力，则它将沿着直线O—a，直至达到抗拉强度，然后是拉伸软化曲线a—b。如果荷载在点
处再次反转，则裂缝张开和闭口曲线b—f和直线f—g—3，直到再次达到压应力包络线，其中f（εfp，σfp）是应力为0.1fco时压应力包络线的公共点。用于描述裂缝开闭效应的曲线最初是由Menegotto和Pinto（1973）开发用于钢筋的，但其性能使其适用于当前的应用。该曲线的方程表示为
式中，
；常数R0，a1和a2分别取20，18.5和0.0015。
2.等效单轴应变
等效单轴应变是一种虚拟应变，没有真正的材料意义。Darwin和Pecknold（1977）首先引入了这一概念，将多轴材料响应解耦合为正交各向异性单轴响应。对于给定的一组应力σi（i=1，2），等效单轴应变εei是在等效单轴应力-应变曲线上引起相同应力的应变。主应变方向上的等效单轴应变和相应的割线刚度可以根据增量法得出（Ayoub，1998）：
式中，εi是方向i上的主应变；εei是方向i上的等效单轴应变；ν是泊松比；σi是主应变方向i上的应力；Ei是主应变方向i上的割线模量；t是结果收敛时先前的迭代次数，t＋1是当前的迭代次数。
3.材料刚度矩阵
正交异性主轴上的两个正应力和剪应力对应的局部材料刚度矩阵DLocal形式（Chen 1976）如下：
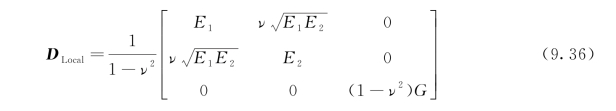
式中，G是割线剪切模量。
割线剪切模量G和泊松比ν分别取为
式中，νi为方向i上的泊松比，如ν1表示方向1上的一个单位应变对方向2的影响。泊松比νi可以用方向i上的等效单轴应变εei和初始泊松比来表示。如果εei是拉伸，则νi将其作为初始泊松比ν0，并在开裂后的范围内减小到零，包括裂缝开启和关闭曲线。如果εei是抗压的，νi则由Kupfer等人（1969）提出的公式计算，这是有试验数据支持的，即：
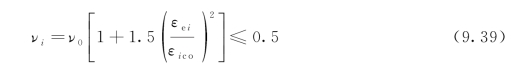
式中，εico是在方向i处的压应变。
然后通过适当的变换获得材料整体刚度矩阵DGlobal，即
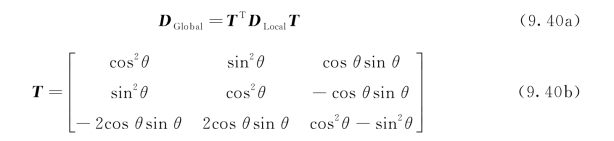
式中，T是转换矩阵；θ是从局部正交各向轴到全局轴的旋转角度，逆时针旋转为正。
4.单元刚度矩阵
采用如图9.13所示的四节点矩形线性位移单元，在确定了材料整体刚度矩阵DGlobal后，可以采用2×2高斯积分方案，按照标准有限元方法（Cook，2001）计算单元刚度矩阵。
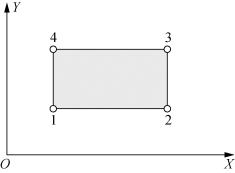
图9.13 混凝土四节点矩形单元
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
