混凝土断裂力学：Baant和Oh的裂缝带模型

Rashid（1968）最早提出了基于弥散裂缝框架的考虑混凝土应变-软化行为的一种模型。Bažant和Oh（1983）在Hillerborg等人（1976）的基础上提出了裂缝带模型（CBM），其假设有限元的断裂过程区中分布着一群紧密平行排列的裂缝。材料特性通过应力-应变本构关系表征，并根据断裂能和单元尺寸计算得出。假设断裂过程区的宽度（hc）为常量，对于普通混凝土而言，假设其值大约为集料尺寸的3倍。让断裂带的宽度保持不变是为了避免伪网格敏感性，这确保了断裂过程中单位长度的裂缝所需的能量损耗保持不变，且刚好等于材料常数断裂能（GF）。在该模型中，通过将各向同性弹性模量矩阵变为正交异性弹性模量矩阵来模拟裂缝，从而合理模拟了减小了的开裂面垂直方向上的刚度。通过在弹性应变上叠加断裂应变εf来模拟混凝土的软化行为。Bažant和Oh（1983）给出了该模型在笛卡尔坐标系（直角坐标系）中的简要数学基础，如图9.9所示。如果混凝土被理想化为匀质材料，那么三轴应力-应变关系由下式给出：

式中，σx、σy和σz为主应力；εx、εy和εz为主应变；εf为微裂缝张开引起的（附加）断裂应变；E是混凝土的杨氏模量；ν为泊松比。

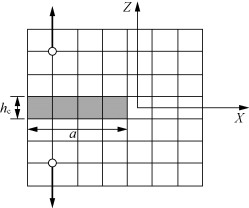
图9.9　裂缝带模型

当材料中的微裂缝发展时，微裂缝的张开并不对X方向和Y方向（Y方向垂直于裂缝表面，见图9.9）的应变造成影响。假设断裂带宽度hc为材料常数，由试验确定，并与素混凝土的集料尺寸成比例。断裂应变εf通过所有微裂缝引起的变形求和确定，是与Z轴相交的微裂缝引起的变形总和。直线裂缝上正应力σz的相对位移δf为

当裂缝尖端的应力达到拉伸强度时，开始发生断裂行为，此时εf仍为零。当裂缝张开时，δf开始增加，而σz则逐渐减小。建模的简便方法是选择线性函数，如图9.10所示。

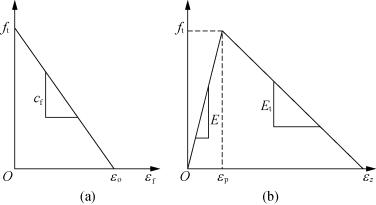
图9.10　CBD的应力-应变关系

断裂应变εf可以表示为关于应力σz的函数：

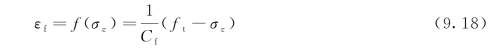
式中，Cf=ft/εo，εo是应变软化曲线的端点应变值，应变达到该点时，微裂缝聚集形成连续的裂缝，同时σz消失。由式（9.18），将式（9.16）修正为

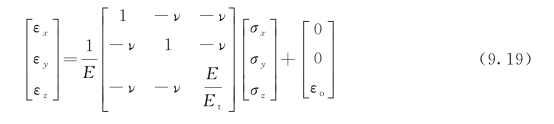(www.xing528.com)

荷载峰值之后的应力-应变关系由切线模量Et描述，由下式给出：

定义形成裂缝所需要吸收的能量为断裂能GF，由下式给出：

积分式表示应力达到ft之后应力-应变曲线包围的面积。假设应力-应变之间为线性关系，那么有：

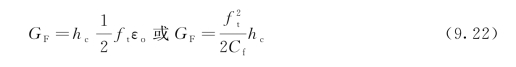
如果GF、ft和hc由试验已知，那么应力-应变关系的基本参数可由下式计算：

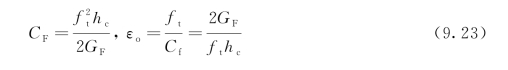
同样地，断裂能也可由应力-应变关系的总面积表达。利用式（9.20）可得：

裂缝带模型是一种弥散裂缝方法，它基于传统连续介质力学的概念，其本构关系是随着局域化最小尺寸而变的软化应力-应变曲线。该裂缝带宽度本质上是一个处理的数值，需要根据特定的问题来准确确定。

裂缝带模型也存在一些局限（Bažant和Lin，1989），例如，①网格划分的尺寸不能小于断裂区宽度；②锯齿形的裂缝带扩展需要特殊的数值处理；③对于斜裂缝，方形网格会导致一定程度的方向偏差。为了改善这些缺陷，Bažant及其团队发展出了非局域弥散裂缝等方法（Bažant，1986，2002；Planas等，1993a；de Borst，2003；de Borst等，2004）。