混凝土断裂力学：有限元离散

CCM（FCM）假定FPZ在二维和三维分析中分别坍塌成线和面。纯Ⅰ型加载时，当一个单一的宏观裂缝在固定方向张开时，黏聚裂缝可以很容易地通过Petersson（1981）提出的方法模拟，由Carpinteri（1989a，b，c）以及Planas和Elices（1991）进一步修改。在这种方法中，沿着潜在裂缝线，断裂节点的数量保持不变，取决于前处理中建立的模型。在有限元执行时，沿着潜在断裂线，裂缝张开节点从底部到顶部依次标记为1和n，如图9.4所示。

为了方便起见，沿着潜在断裂区n个节点的裂缝张开位移列向量以下面的形式表达：

图9.4　混凝土Ⅰ型张开裂缝的黏聚裂缝扩展模拟

式中，{w}是n阶断裂节点的裂缝张开位移向量；[K]是对称矩阵，Kij是作用在j断裂节点的单位力引起的i断裂节点的裂缝张开位移；{p}是节点力向量；{C}是P=1时n阶断裂节点的裂缝张开位移向量；{pg}是试件自重引起的n阶断裂节点裂缝张开位移向量。

使用增强影响法（Planas和Elices，1991）来求解式（9.5）。假设断裂节点总数为n，初始裂缝尖端位于第k个节点，根据增强影响法，式（9.5）可以分割为缺口部分的节点i=1，2，3，…，（k－1）和连接部分的节点i=k，（k＋1），（k＋2），…，n。那么，分割后的式（9.5）可以写成如下形式：

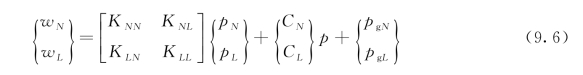
下标N和L分别表示缺口部分的i=1，2，…，（k－1）和连接部分的i=k，（k＋1），（k＋2），…，n。由于连接区裂缝开口宽度为零，而初始缺口部分为无牵拉区，故可写成：

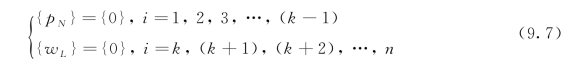
式（9.6）和式（9.7）可以写成：

其中，

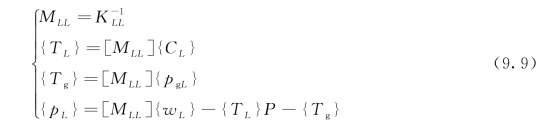(www.xing528.com)

此外，沿着断裂线，纽带部分可以分割为黏聚（受损）区和未破裂（未受损）区。假设黏聚区节点是j=k，（k＋1），…，l，未受损区节点为j=（l＋1），（l＋2），…，n。因此，在进一步分割式（9.7）之后，可以写成：

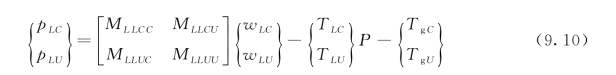
下标C和U分别表示黏聚区的j=k，（k＋1），…，l和未受损区的j=（l＋1），（l＋2），…，n。未受损区和黏聚区的最后一个节点的裂缝张开位移为零，在数学上可以表示为

根据式（9.10）和式（9.11）得出：

对于j=lth节点，施加的荷载P可以写成以下形式：

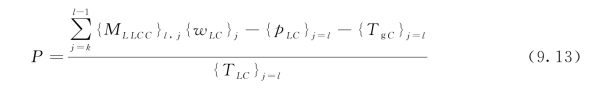
对于节点j=k，（k＋1），（k＋2），…，（l－1），使用式（9.12）和式（9.13），随着黏聚区裂缝的张开，可以形成许多非线性联立方程，其函数形式可以表示为

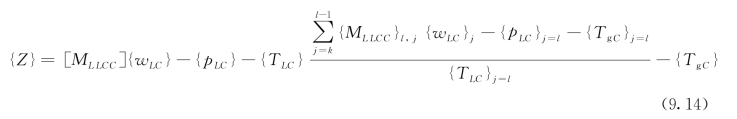
采用适当的符号规约，则可以写为{pLC}=－Fuc f（wLC），对于规则离散化为均匀网格尺寸h的情况，除了i=k和i=n之外，对于所有i值，Fuc=Bhft；对于i=k和i=n，Fuc=。式（9.14）可用牛顿-拉夫逊方法求解，求解式（9.14）得到{wLC}，再分别使用式（9.13）和式（9.12）确定P和{pLC}。返回到式（9.11）—式（9.5），可以确定{w}和{p}的所有未知值。

对于已知的{p}和P的值，梁的跨中挠度δ可以由下式确定：

式中，DL是外部荷载P为单位力时加载点的挠度；{Dp}是单位荷载矢量{p}={1}时的加载点挠度矢量；Dg是由试件自重引起的加载点挠度。