混凝土断裂力学：裂缝扩展KR阻力曲线

根据图8.7读取与三个样本（B250－80b，B150－80b和B63－80b）加载点相关的CMOD试验数据。应用解析法[式（8.5）]计算裂缝扩展阻力作为参考值，与应用权函数法计算得到的裂缝扩展阻力值进行比较。因为在积分边界存在一个奇异问题，可以用高斯-切比雪夫正交数值方法求解式（8.5）。如果使用权函数法的闭合表达式[式（8.13）或式（8.15）]，则可以避免使用该数值积分方法。结果表明，使用四项式通用权函数计算双K断裂参数误差可以控制在2%以内，而用五项式通用权函数可以得到几乎相同的结果。

为了验证当前权函数法，在确定裂缝扩展阻力时仅采用四项式权函数。在该方法中，首先用式（4.23）和表4.1计算四项权函数的三个参数M1，M2和M3。初始韧度值用式（8.5）的解析法计算。使用四项权函数的闭合表达式（8.13）计算裂缝扩展阻力。在荷载达到峰值前的每个阶段，沿虚拟裂缝的Δac计算值满足式（6.15）。

研究发现，非线性软化函数中材料常数c1，c2和wc的选择会影响KR曲线。考虑这些材料参数时，采用试错法，其中c1和c2的值始终保持为常数3和7，wc的值则可以是160μm，150μm和140μm。例如，图8.8展示了尺寸为150 mm的试件，使用权函数法获得的wc值对KR曲线的影响。从图中可以看出，KR曲线受到wc值的影响，特别是对于尺寸为63 mm的试件，与K曲线相比，在wc为150μm和160μm时，KR值出现了不合理的错误。因此，根据最终计算，参数c1，c2和wc分别取3μm，7μm和140μm。这个假定也比较合理，因为混凝土的抗拉强度计算值是3.805 MPa，与假设wc值为140μm时抗拉强度的计算值4.12 MPa接近（Phillips和Zhang，1993）。

使用解析法[式（8.5）]和权函数法[式（8.13）]所获得的全部三个不同尺寸梁试件（63 mm，150 mm，250 mm）的裂缝扩展阻力KR（Δa）和裂缝尖端的应力强度因子K（P，a）与裂缝扩展增量Δa的关系如图8.9—图8.11所示。相应的荷载P与裂缝扩展增量Δa的关系曲线也显示在图中。图8.9—图8.11分别对应于尺寸为63 mm，150 mm和250 mm试件的断裂行为。符号B，B＇，C，C＇，ΔaB和Δac用来表示这些图上的特征点。比较式（8.5）与闭合表达式（8.13）所获得的KR曲线可以发现，三个样本在裂缝扩展的任意值处都没有明显的差异，计算值只能观察到一个极小的数值差异。如果考虑五项式权函数法[式（8.15）]，这个差异还可以更小，可以获得数值上几乎相同的裂缝扩展阻力。因此，式（8.13）或式（8.15）可以直接用于准确地计算混凝土结构的裂缝扩展阻力。

因为解析法的积分边界存在奇异性问题，使用权函数法的这些闭合表达式可避免特殊的数值积分情况。此外，权函数法的这些表达式在计算机程序中的实现流程更简单，裂缝扩展阻力的计算效率得到了提高。值得指出的是，使用解析法计算断裂参数的准确性取决于数值积分的步长。特别是使用双线性软化函数时，如果选择的积分点数相对较少，或者积分点的位置相对远离转折点，解析法将可能导致一定程度上的误差。而式（8.13）是一个闭合解，不存在这种误差。

图8.8　非线性软化参数wc对KR曲线的影响

(www.xing528.com)

图8.9　KR曲线对比及裂缝扩展的稳定分析（63 mm）

图8.10　KR曲线对比及裂缝扩展的稳定分析（150 mm）

图8.11　KR曲线对比及裂缝扩展的稳定分析（250 mm）

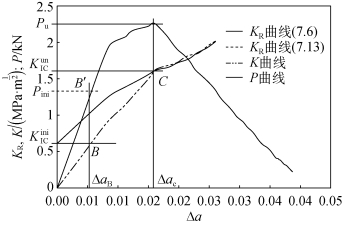
从图8.9—图8.11可以看出，KR曲线和K曲线之间的相互比较可以当作一个断裂准则，来描述断裂全过程中裂缝稳定扩展的条件。从这些图中可以看到，在P－Δa曲线的上升段，K曲线的值低于KR曲线的值。这意味着，裂缝在P－CMOD曲线的上升段为稳定扩展，直到裂缝延伸长度达到ac。在P－Δa曲线的下降段，K曲线则高于KR曲线，这意味着裂缝扩展是不稳定的。在峰值荷载处，KR曲线等于K曲线的值，对应于不稳定裂缝扩展的开始。

KR曲线的起点对应的是材料的初始韧度，荷载峰值点则对应的是材料的断裂韧度。因此，裂缝扩展的稳定性可以用双K参数和来描述。从KR曲线分析可知，是材料的固有韧度，对应KR曲线在B点处的起始点。过纵坐标绘制一条与Δa轴平行的水平线，直到穿过K曲线。从B点绘制一条垂直线直到它在B＇点切断P－Δa曲线。B＇点给出了起始裂缝荷载Pini，类似地，从KR曲线和K曲线的交点（点C）绘制一条与Δa轴平行的线，与纵轴的交点称为不稳定断裂韧度。如果从交点C画一条垂直线，直到它穿过P－Δa曲线并交于点C＇，对应的荷载点即为峰值荷载。与相关的裂缝扩展长度Δa是临界等效裂缝长度。Δac－ΔaB的值是临界宏观裂缝延伸长度，即稳定缓慢发展裂缝的增加长度。实际上，断裂全过程可用双K断裂准则描述，这与KR曲线断裂准则是等价的。