混凝土断裂力学试验结果及分析

Xu和Reinhardt（1998）使用了一共8个标准切口的混凝土梁试验，这些梁的尺寸和初始裂缝长度/深度比（a0/D）各不相同。在这8个试件中，有1个试验梁来自Karihaloo和Nallathambi（1991），有4项结果取自Refai和Swartz（1987），有3个试验梁来自Jenq和Shah（1985）。从这些计算结果发现，KR曲线不依赖于样本尺寸和初始裂缝长度/深度比（a0/D）。

本节主要目标是用解析法验证权函数法，以确定基于黏聚力分布的KR曲线。采用Roesler等人（2007）公布的一组试验结果，名称分别为B250－80，B150－80和B63－80，其包括完整的P－CMOD曲线，分别对应于梁深250 mm，150 mm和63 mm三种情况。表8.1汇总了试验结果的主要特征以及材料特性。图8.7显示了试验的平均P－CMOD曲线。混凝土的抗拉强度用关系式MPa（Karihaloo和Nallathambi，1991）确定。

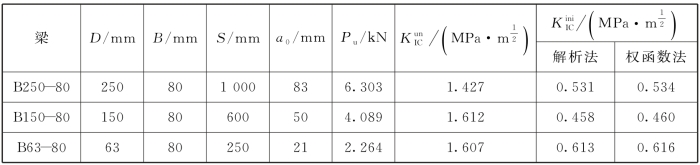
表8.1　切口混凝土梁的试验参数和计算结果（E＝32 GPa，fc＝53.8 MPa）

(www.xing528.com)

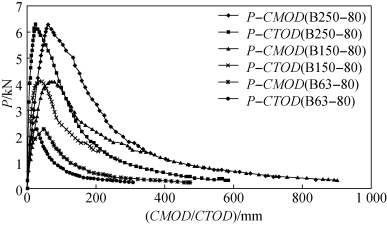
图8.7　P－CMOD平均包络线以及计算得到的P－CTOD曲线

实际上，非线性软化函数中的材料常数值应该由单轴拉伸试验来确定。当缺乏试验数据时，普通混凝土的非线性软化参数值c1，c2和wc可以分别取3μm，6.93μm和160μm（Reinhaedt等，1986）。此外，当抗拉强度在2.93~4.12 MPa范围内时，混凝土wc的值可以取100~140μm，（Phillips和Zhang，1993）。Xu和Reinhardt（1998）对研究中报道的三种混凝土混合物采用了试错法来确定常数c1，c2和wc。

在KR曲线的计算中（Xu和Reinhardt，1998），对Refai和Swartz（1987）测试的混凝土，c1，c2和wc分别取3μm，7μm和100μm；对Jenq和Shah（1985）测试的混凝土，c1，c2和wc分别取3μm，7μm和140μm；对Karihaloo和Nallathambi（1991）测试的混凝土，c1，c2和wc分别取2μm，13μm和100μm。在下面求解KR曲线的讨论中，Reinhardt和Xu（1999）使用的材料参数c1，c2和wc分别为3μm，10μm和110μm。