混凝土断裂力学计算公式

1.情况1：a=a0

因为黏聚应力分布σ（x）=0，黏聚韧度对总的裂缝增长阻力没有贡献，仍然等于。

2.情况2：a0≤a≤ac

对于这种荷载状况（a0≤a≤ac或0≤CTOD≤CTODc），黏聚力分布由式（8.6）表示。参考图8.3，为

式（8.16）可以直接用式（8.13）和式（8.15）来进行求解，其中C1=σ（wt），C2=。

3.情况3：ac≤a≤awc(www.xing528.com)

对于这种裂缝扩展情况（图8.4），黏聚力分布采用式（8.7）所示的双线性形状。因为应力分布σ1（x）和σ2（x）而产生的黏聚韧度的两个部分分别计算，相加成为总黏聚韧度：

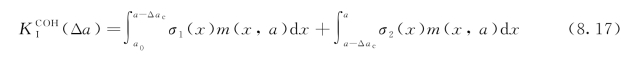
式（8.17）可以用式（8.13）或式（8.15）来求解，其中，与黏聚力σ1（x）相关的是C1=；与σ2（x）相关的是C1=。

4.情况4：a≥awc

这种情况的荷载条件如图8.5所示，黏聚应力分布由式（8.10）表示。黏聚韧度对裂缝扩展阻力的贡献为

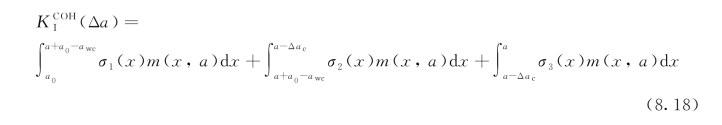
根据权函数中的项数，黏聚韧度用式（8.13）或式（8.15）进行计算。需要考虑三种相应的应力分布，即σ1（x），σ2（x）和σ3（x）。因为σ1（x）=0，则由黏聚应力σ1（x）贡献的韧度为0。对黏聚力Δac），这些值将用于式（8.13）或式（8.15）。然而对黏聚力σ3（x），这些值是C1=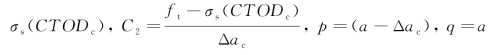。一旦的值用式（8.13）或式（8.15）求解，裂缝扩展阻力KR（Δa）就可以根据式（8.3）计算出来。