混凝土断裂力学：黏聚韧度的闭合表达式推导

为了计算裂缝扩展阻力，在断裂过程区中考虑一种线性应力分布的广义情况，如图8.6所示。假设当总的裂缝扩展长度为a时，黏聚力作用在裂缝长度p和q之间。裂缝长度p和q处的黏聚应力大小分别为σp和σq。因此，在任意裂缝长度x处，黏聚力的分布用以下形式表示：

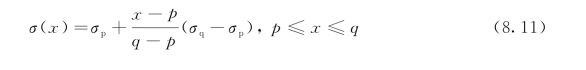
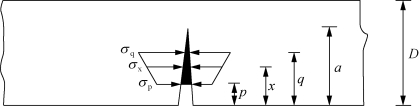
图8.6　裂缝扩展期间虚拟断裂带中黏聚力的分布（p≤x≤q）

式（8.11）中，令C1=σp且，裂缝扩展期间虚拟裂缝中黏聚力分布所产生的黏聚韧度用式（4.1）计算得到以下表达式：

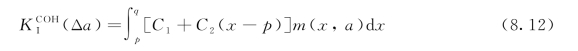
使用式（4.22）中四项式权函数，结合式（8.12）可以推导出的闭合解形式如下：

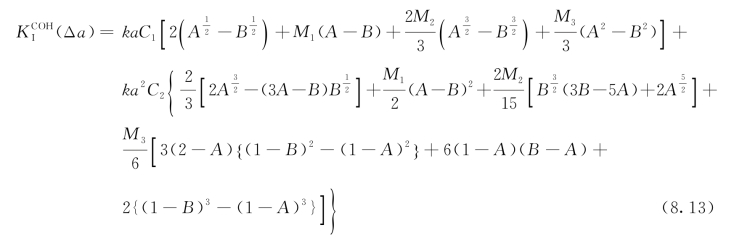(www.xing528.com)

其中，

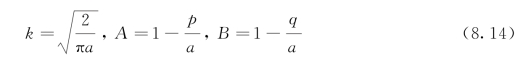
如果考虑五项式权函数，如式（4.24）所示，的值可由式（8.12）确定，闭合解的形式表达如下：

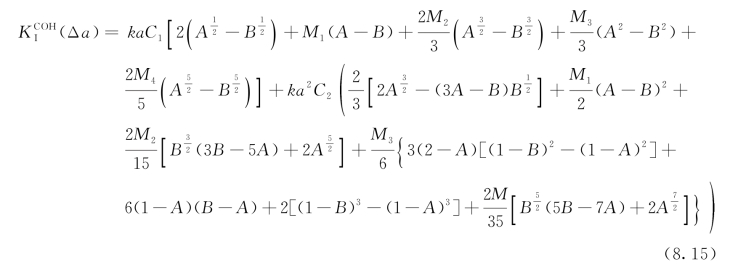
这里提出的权函数法是基于黏聚力分布来求解裂缝扩展阻力的一种替代方法，权函数法不需要特别的数值积分方法来获得KR曲线。在第5章中介绍了一种使用权函数的类似方法来获得双K断裂模型的断裂参数，其中黏聚韧度的闭合表达式被推导出来，针对虚拟断裂带中的黏聚力为梯形分布的情况，但不适用于黏聚力双线性变化的区域。

式（8.13）和式（8.15）则是以一种更广义的方式推导得到的，不同于之前提出的那些公式。确切地说，第5章中列出的公式是式（8.13）和式（8.15）的特例，且仅适用于作用在过程区全长（a－a0）上黏聚力为线性变化的情况。而式（8.13）和式（8.15）则适用于作用在过程区部分或全长上的黏聚力为线性和双线性分布的情况。

根据裂缝扩展的四个阶段，黏聚韧度引起的裂缝扩展阻力可以用式（8.13）或式（8.15）来确定。在裂缝扩展的每个阶段，扩展裂缝长度a、黏聚应力分布（即常数C1和C2）、过程区范围以及黏聚力沿着裂缝作用值（p和q）在式（8.13）和式（8.15）中都是不同的。