混凝土断裂力学：快速求解KR曲线

与虚拟断裂带的黏聚力分布相关的断裂全过程中，裂缝扩展阻力的一般表达式（Xu和Reinhardt，1998；Reinhardt和Xu，1999）如下：

式中，是格林函数。对于三点弯曲（TPBT）试件，则有：

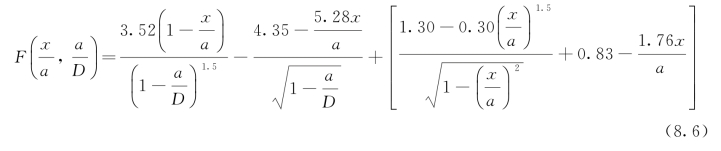
根据图8.2中出现的裂缝扩展情况，裂缝扩展阻力可以用式（8.5）来确定。在加载的每一个阶段，扩展裂缝的长度不同，黏聚力分布形式在式（8.5）中都不相同，可分成下列四种情况。

1.情况1：a=a0

在此加载阶段，初始缺口长度不会增长，物体仍保持弹性状态，承受小荷载（直至Pini）无任何缓慢的裂缝扩展。因此，黏聚应力σ（x）=0且裂缝扩展阻力仍与材料的初始韧度相等，为垂直于水平坐标的垂直线。KR（Δa）的值为

2.情况2：a0≤a≤ac

在此加载阶段，结构表现为稳定缓慢的裂缝扩展，直到与荷载最大值Pu相关的临界裂缝长度值ac。在临界情况下，CTOD=CTODc，如图8.3所示。在这期间，a0≤a≤ac，0≤CTOD≤CTODc，黏聚力的分布近似为线性。黏聚力沿虚拟裂缝带的变化可表示为

式中，σ（wt）为黏聚应力值；wt为初始缺口尖端处的裂缝张开位移。

σ（wt）的值是由混凝土的软化函数确定的。根据KR曲线法的上述发展过程，虚拟断裂带中只有两个黏聚应力值σ（wt）和σs（CTODc）需要被确定。

(www.xing528.com)

图8.3　裂缝扩展期间虚拟断裂带中黏聚力的分布（a0≤a≤ac）

3.情况3：ac≤a≤awc

在此加载阶段，施加的荷载P、CTOD的值、虚拟裂缝长度分别比Pu、CTODc的值和临界虚拟裂缝长度ac增大。黏聚力分布表现为双线性，如图8.4所示，表达式如下：

裂缝扩展阻力可以通过式（8.5）获得，积分区域应该分为两步：a0≤x≤（a－Δac）范围内的黏聚力σ1（x）和（a－Δac）≤x≤a范围内的黏聚力σ2（x）。

图8.4　裂缝扩展期间虚拟断裂带中黏聚力的分布（ac≤a≤awc）

4.情况4：a≥awc

这种情况出现于P－CM OD曲线在下降段时相应的荷载状况。当虚拟裂缝长度为awc时，黏聚力分布的完整形状得以发展，并且随着裂缝进一步扩展，初始缺口尖端前面还形成了一个新的无应力裂缝。在这种情况下，应力分布如图8.5所示，用下列关系式表示：

图8.5　裂缝扩展期间虚拟断裂带中黏聚力的分布（a≥awc）

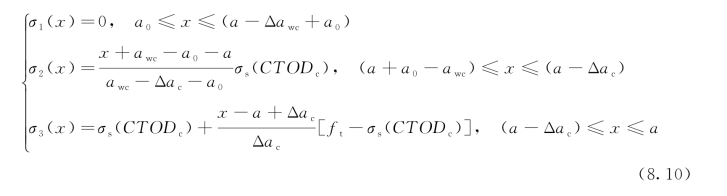
与情况3相似，这种情况下的裂缝扩展阻力也用式（8.5）和格林函数来求解。