混凝土断裂力学：确定DKFM方法的对比

使用FCM获得的TPBT和CT试件在a0/D比值为0.15~0.80和D=200 mm情况下的P－CMOD和P－COD曲线分别如图6.9和图6.10所示。双K断裂参数使用解析法、简化法和权函数法（包括四项式和五项式）计算。使用解析法和权函数法计算ac时均采用试错法。使用简化法的经验公式来确定TPBT和CT试件的ac值。

对于D=200 mm的TPBT和CT试件，使用LEFM公式和简化经验公式确定的无量纲参数与a0/D的关系如图6.11所示。直到a0/D=0.75时，由简化法和解析法求解的TPBT试件的最大差别为3.25%，在a0/D=0.8时略高一些，为5.34%。在不同a0/D下计算得到的平均值的差别在0.13%。对于CT试件，这个最大差别直到a0/D=0.8时仍为0.31%，而对于平均值的差别为0.26%。从图中还可以看出，结果不受试件形状太大的影响。直到a0/D=0.6时，的值几乎保持恒定，超过这个值，两种试件的值都观察到略有下降。这两种几何形状之间平均值的差异约为1.76%。

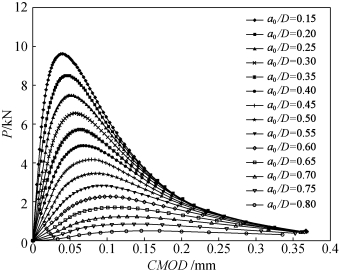
图6.9　D=200 mm，TPBT试件的P－CMOD曲线　

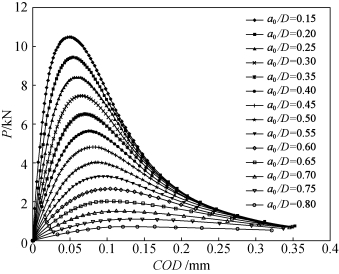
图6.10　D=200 mm，CT试件的P－COD曲线

图6.11　解析法和简化法获得的TPBT和CT试件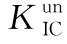（D=200 mm）

针对D=200 mm的TPBT试件，图6.12对比了使用不同方法得到的无量纲量和与a0/D的关系曲线。与随a0/D的变化趋势十分相似。将权函数法和简化法获得的结果与标准解析法确定的结果进行对比，可以发现，在a0/D较大时简化法会有更大的差异。对于尺寸为200 mm的试件，使用四项式和五项式权函数法以及简化法获得的平均值的百分比差别分别为0.85%，0.07%和0.78%。计算值的差别分别为1.62%，0.13%和1.86%，如图6.13所示。在图6.14和图6.15中，对于D=200 mm的CT试件，可以观察到类似结果。从图6.14可以发现，与解析法相比，采用四项式和五项式权函数以及简化法求得的平均值的百分比差别分别为0.89%，0.07%和0.78%。从图6.15可以发现，使用四项式和五项式权函数以及简化方法求得的平均值的差别分别为1.61%，0.13%和1.52%。(www.xing528.com)

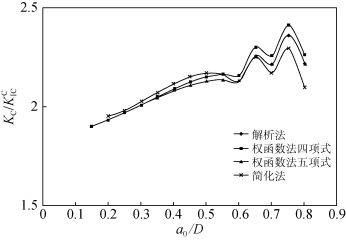
图6.12　解析法、权函数法、简化法获得的TPBT试件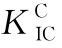（D=200 mm）

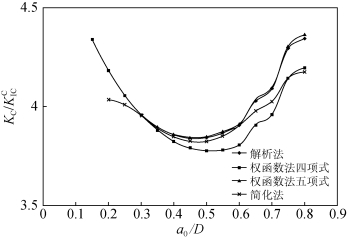
图6.13　解析法、权函数法、简化法获得的TPBT试件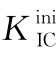（D=200 mm）

图6.14　解析法、权函数法、简化法获得的CT试件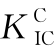（D=200 mm）

图6.15　解析法、权函数法、简化法获得的CT试件（D=200 mm）