【摘要】：Xu和Reinhardt提出了计算黏聚韧度的简化方法，该简化方法是通过校正函数以及式计算得到。式中的F由式计算，FCIC的值由式和式获得。对于0.6≤γ≤0.7，0.2≤α0≤0.8，α直到0.975的情况，可以查阅有关文献。采用解析法和简化方法计算无量纲量，比较结果表明，简化方法计算结果的最大误差小于3.6%。
Xu和Reinhardt（2000）提出了计算黏聚韧度
的简化方法，该简化方法是通过校正函数
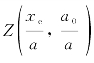以及式（4.13）计算得到。分布的黏聚应力σ（x）被转换成单个的等效力Pe，如图6.6所示。
的绝对值可用下式表示：
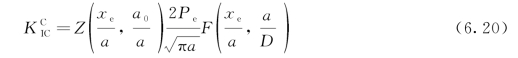
在式（6.20）中，令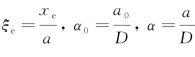
，则无量纲值
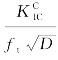为
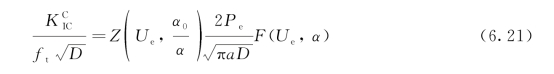
对于梯形黏聚应力分布的情况，使用无量纲系数γ：
则式（6.14）可用无量纲形式表示为
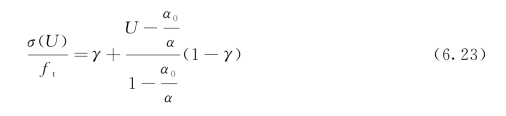
从图6.6可以看出，合力Pe可以写成以下形式：
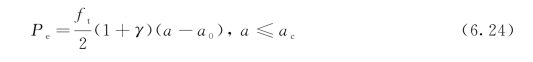
若写成无量纲形式，则式（6.24）可表达成：(www.xing528.com)
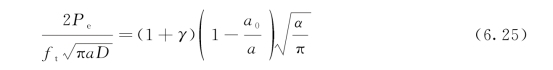
从扩展裂缝尖端测得的黏聚力合力的形心d可通过下式求得：
以及有：
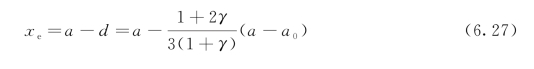
并有：
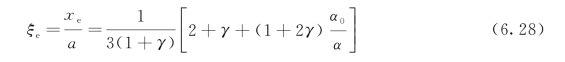
最后，校正函数由以下经验式确定：
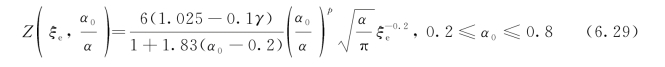
式中，当0.2≤α0≤0.6时，p=1.5（α0－0.2）＋0.8；当0.6≤α0≤0.7时，p=3（α0－0.6）＋1.4；当0.7≤α0≤0.8时，p=6（α0－0.7）＋1.7。
式（6.21）中的F（ξe，α）由式（6.19）计算，FCIC的值由式（6.21）和式（6.29）获得。对于0.6≤γ≤0.7，0.2≤α0≤0.8，α直到0.975的情况，可以查阅有关文献（Xu和Reinhardt，2000）。采用解析法和简化方法计算无量纲量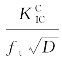
，比较结果表明，简化方法计算结果的最大误差小于3.6%。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
