混凝土断裂力学:探究尺寸效应式的成果

Bažant等（Bažant，1984，2002；Bažant等，1986，1991；Bažant和Kazemi，1990，1991；Gettu等，1990；Bažant和Jirâsek，1993）提出了描述混凝土类材料断裂行为特征的尺寸效应模型，该模型包含两个断裂参数：无限大尺寸试件的断裂能Gf和临界等效裂缝长度cf。这两个断裂参数可根据不同尺寸的几何相似缺口试件最大极限荷载Pu确定，即不需要力-位移曲线。

设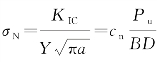， 其中σN为名义强度，a为裂缝长度，Pu为结构的极限荷载，cn为一个与应力强度因子有关的系数，B为平面结构的厚度，D为结构的特征尺寸，如梁高或板宽。同时，设总势能为），其中，对于平面应变问题，E＇=E，对于平面应力问题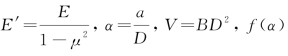是一个与裂缝特征长度比 有关的一个函数。因此能量释放率，其中，因此有：

式中，。对于标准试件，g（α）可在相关手册中查到（Tada等，1985），对于复杂形状也可以通过线弹性有限元分析得到。

按照Bažant的假设，能量释放率G和等效弹性裂缝长度cf将取决于断裂过程区的尺寸，并且与极限荷载时刻近似存在相似关系，因此有将g（α1）按照泰勒级数在处展开，取前两项，则有，将其代入式（5.8）可以得到：

令可得Bažant尺寸效应模型的一般形式如下：

当D⇒∞，则有α⇒α0，联合式（5.10）和式（5.8）可以得到无限大尺寸试件的断裂能Gf：

对于较小尺寸的情况，D⇒0，因此式（5.10）中β⇒0，联合式（5.10），据此也可以得到。

式（5.10）中的β又称为脆性指数，同时可引入参数，其表达式为

(www.xing528.com)

尺寸效应模型的一个优点是，无限大尺寸试件的断裂能Gf和临界等效弹性裂缝长度cf可以通过对几何相似结构的最大极限荷载Pu进行回归分析获得。RILEM方法（1990b）描述了如何利用尺寸效应模型，基于回归分析，确定非线性断裂特性。将式（5.10）扩展变化为

令则有：

在X－Y坐标系中绘制Y和X的关系，如图5.8所示。式（5.14）中的系数通过线性回归分析确定，分别取回归线斜率的变异系数和截距的变异系数。离散带的相对宽度不超过0.1，0.2和0.2。断裂能Gf、等效弹性裂缝长度cf和脆性指数β分别由下式计算：

图5.8　试验数据回归分析

通常当β>10时，可以通过线弹性断裂力学来进行断裂分析；当β<0.1时，则可以通过强度理论来预测断裂行为；当0.1≪β≪10时，结构需要根据非线性断裂力学来分析。

另外，R阻力曲线和裂缝扩展过程中的裂缝增量可由下式确定：

尺寸效应模型中定义的断裂能Gf与试件形状和尺寸无关，但实际上它只是一种近似描述。该模型近似地描述了介于无尺寸效应的强度理论和尺寸效应显著的LEFM准则之间的过渡区。具有简单性是尺寸效应法的一个重要的优势，它只需要知道几何相似的不同尺寸试件的最大荷载值，不需要采用专门的闭路试验系统。既不需要确定峰值荷载后的软化响应，也不用知道裂缝的实际长度。尺寸效应法的另一个优点是，它不仅可以获得材料的断裂能，还能得到断裂过程区的等效弹性裂缝长度。

需要指出的是，尺寸效应式（5.9）和式（5.10）是在式（5.8）的级数展开式中取一次项，因此，当构件特征尺寸W偏大时，式（5.9）和式（5.10）相对于式（5.8）将会有一定的精度损失。另外，与线弹性断裂力学尺寸效应式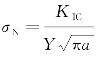相比较而言，Bažant尺寸效应式在几何尺寸趋于零时将得到一个确定的值，而线弹性断裂力学尺寸效应式将会趋于无穷大，显然Bažant尺寸效应式在极小尺寸范围内对尺寸效应的描述比线弹性断裂力学尺寸效应式更加符合实际。