混凝土断裂力学-断裂参数确定

为了确定两参数断裂模型中的两个断裂控制参数，首先需要确定最大荷载时刻的等效弹性裂缝长度（即临界等效弹性裂缝长度ac）。临界等效弹性裂缝由两部分组成：第一部分是初始裂缝，第二部分是加载到峰值时刻的等效扩展裂缝长度。由于很难直接测量裂缝尖端张开位移（CTOD），故一般采用测量裂缝口张开位移（CMOD）的办法进行反算。

如图5.4所示，在超过0.5倍峰值荷载并且未达到峰值荷载时的P－CMOD曲线会呈现出较明显的非线性特征，这主要是由于混凝土裂缝尖端断裂过程区中的亚临界裂缝扩展造成的。两参数断裂模型认为，随着这种亚临界裂缝扩展，体系将产生非线性变形。也就是说，P－CMOD曲线在非线性部分的任何一个阶段，裂缝口张开位移（CMOD）可以分解为弹性部分（CMODe）和塑性部分（CMODp）之和，即CM OD=CMODe＋CMODp。与之相对应的裂缝尖端张开位移（CTOD）分解为弹性部分（CTODe）和塑性部分（CTODp）之和，即CTOD=CTODe＋CTODp。

两参数断裂模型中的临界等效弹性裂缝长度ac定义为与裂缝口张开位移（CM OD）的弹性部分（CM ODe）相对应的等效裂缝长度。因此，两参数断裂模型采取峰值荷载卸载法获得CMODe（该方法称为卸载柔度法），并将其代入线弹性断裂力学给出的相应公式，确定ac的值。

图5.4　（a）等效Griffth裂缝；（b）P－CMOD曲线

然而事实上，试验中无法准确预知实际结构所能承受的峰值荷载，因此两参数断裂模型放宽了卸载的条件，可选择在峰值后下降不超过5%的荷载阶段卸载来获得CMODe。值得指出的是，在两参数断裂模型中，临界裂缝口张开位移CTODc实际上指的是弹性部分CMODe对应的，在绝大多数的参考资料中简化为CTODc。

以三点弯曲梁试验为例，根据线弹性力学的解，裂缝口张开位移（CMODe）和弹性裂缝长度ac的关系由下式给出（D为高度，B为厚度，E为弹性模量）：(www.xing528.com)

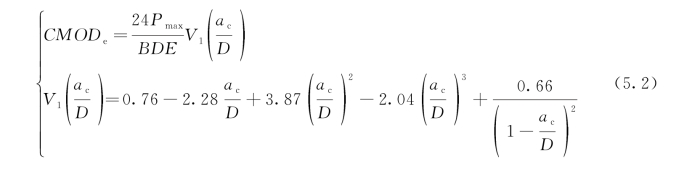
由上述卸载方法得到CM ODe并确定临界等效弹性裂缝长度ac后，就可以根据线弹性力学的解确定两参数断裂模型的两个控制参数和CTODc的值。对于三点弯曲梁试验，计算式如下：

为了便于使用两参数断裂模型研究混凝土断裂的规律，常常将研究曲线归一化处理。脆性指数Q是两参数断裂模型中常用的归一化参数，可采用下式计算：

脆性指数Q越小，则说明材料越脆。对硬化水泥净浆、砂浆和混凝土材料，Q值分别为1.25~5 cm，5~15 cm，15~35 cm。