混凝土断裂力学：5项通用权函数

如果期望得到更高精度的预测，可将式（4.22）修正为五项式通用权函数：

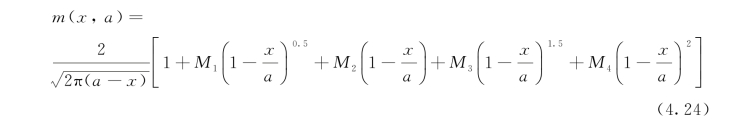
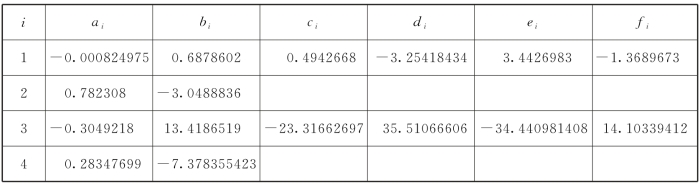
如上文所述，参数M1，M2，M3，M4的值可通过最小二乘法获得。其中，参数M1和M3的数值可由式（4.23）的第一式确定，参数M2和M4可由式（4.23）的第二式确定。相应的系数ai，bi，ci，…，fi由表4.2给出。

表4.2　五项式权函数参数M1，M2，M3，M4的系数值

五项式权函数与格林函数的比较如图4.5所示。通用权函数的最大绝对误差，在裂缝长度范围，当时小于1.5%，当时小于1%。对于的情况，通常不属于工程实践感兴趣的分析范围。(www.xing528.com)

从上述分析可知，四项式通用权函数与标准格林函数的误差小于3%，而五项式通用权函数的误差可以进一步减小到1.5%以下。因此，在工程运用中，对于有限宽板的边缘裂缝，四项式通用权函数替代格林函数不会产生过大的误差。五项式通用权函数可以作为应力强度因子更高精确性预测的替代解决方案。

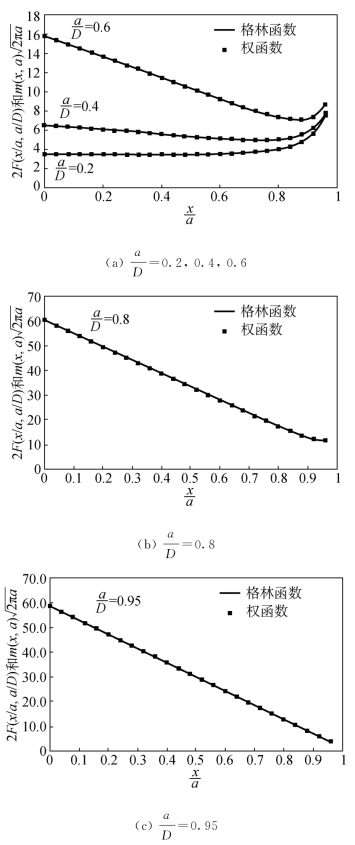
图4.4　不同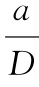取值的对比情况（四项式权函数）

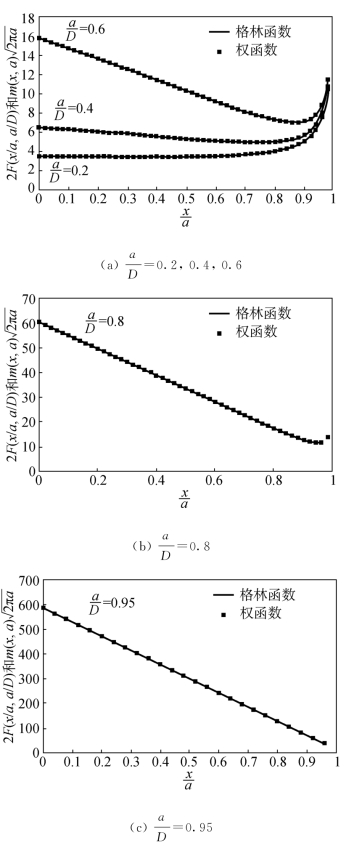
图4.5　不同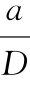取值的对比情况（五项式权函数）

使用通用权函数替代格林函数不仅可以减少确定应力强度因子的时间，并且可以得出工程实践中应力强度因子沿着裂缝线局部应力分布为复杂多项式时的闭合解。由于需要考虑准脆性材料（如混凝土）断裂过程区的黏聚应力，混凝土结构中采用权函数确定应力强度因子可以简化积分表达式，避免使用复杂的数值积分方法。