基于软化函数的混凝土断裂力学

1.线性软化函数

图3.13所示的线性软化函数可以用以下形式表达：

以及

2.双线性软化函数

图3.14所示的双线性软化函数可以用以下形式表达：

软化曲线以下的区域有：

扭结点的无量纲形式的值分别为和，其中σs和ws分别是双线性软化曲线斜率变化点处的纵坐标和横坐标。Petersson（1981）使用和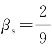的取值，代入式（3.8）得到：

在双线性应变软化图表中，Wittmann等（1988）发现，和的值适合模拟CT试件的P－COD行为。在这种情况下，可以获得以下关系：

CEB－FIP Model Code 1990（1993）引入了各种经验关系以获得双线性软化曲线的不同参数。根据规范，wc和常数kd的值取决于所给集料的最大尺寸da，这些参数列于表3.2。

表3.2　双线性软化曲线的不同参数

对于最大骨料尺寸如19 mm，wc和常数kd采用线性插值，其值为wc=0.1688 mm，kd=6.75。按照CEB－FIP Model Code 1990的规定，αs=0.15的值保持固定，而给定GF时，βs的值可以使用规范中给出的经验公式来获得：

根据式（3.8）和式（3.9）获得以下关系：

双线性软化的特征参数也可由Xu和Reinhardt（1999）以及Xu和Zhang（2008）提出的关系式来确定。这种软化函数可以称为修正的双线性软化函数，在这种情况下，GF可以根据CEP－FIP Model Code 1990中给出的关系式来计算。修改的双线性软化的其他参数如下：(www.xing528.com)

式中，。

3.指数软化函数

指数软化函数（Gopalaratnam和Shah，1985）最初是以下列形式提出的：

式中，λ和k是常数，λ=1.01，k=0.063；w以μm为单位。

一种常用的指数函数形式（Karihaloo，1995）为

式中，μ是材料常数，当σ=0.01ft，w=wc时，有μ=4.6052，wc用下式计算：

4.非线性软化函数

非线性软化关系（Reinhardt等，1986）最初是以下列形式提出的：

式中，c1，c2和wc是材料常数。对于普通混凝土，式（3.17）中的这三个参数可以取c1=3，c2=6.93，wc=160 mm。

wc也可以用式（3.18）中给定的GF和前面的c1和c2计算：

5.准指数软化函数

准指数软化函数（Planas和Elices，1990）由以下表达式给出：

式中，c1，c2是材料常数。