混凝土断裂力学：拉伸行为的应变局域化效应

了解了混凝土的微观结构之后，可以知道混凝土的力学行为具有复杂性，实际情况也是如此，从混凝土拉伸行为的宏观表现即可见一斑。由于材料在裂缝尖端附近承受拉应力，在断裂分析中不可避免需要了解受拉混凝土拉伸断裂的全过程特性。20世纪60年代，许多研究者（Hughes和Chapman，1966；Evans和Marathe，1968）使用大刚度拉伸试验机，通过直接拉伸试验得到了混凝土稳定且完整的应力-位移图。直接拉伸试验中混凝土典型的应力-位移曲线如图3.8所示。

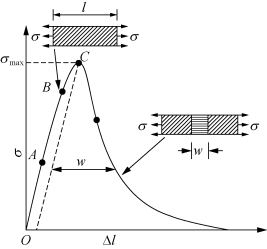
图3.8　混凝土典型的应力-位移曲线

试验结果（Heilmann等，1969）表明，直接拉伸试验中出现了变形局域化这一有趣的现象。当应力到达最大数值后，随着试件变形的增加，试验机的拉力将下降，而增加的变形集中于一个狭小的区段内，在这个区段之外，试件处于卸载状态。这个在后峰下降段变形不断增加的区域即是变形局域化的区域。混凝土的这种拉伸行为中的局域化行为与混凝土微观结构的多相性和不均匀性实际上有着十分密切的关系。

此外，基于声发射和电子散斑图案干涉测量的试验技术证实，在达到峰值荷载前混凝土表现出明显的非线性（Shah和Ouyang，1994）。用图3.8中的A、B、C三个转折点来进行说明。点A对应达到荷载峰值的30%左右，此时应力应变处于弹性关系，点B对应于峰值荷载的80%左右。点A与点B之间混凝土内部的微裂缝扩展是孤立的，并且在试件体积上呈现为随机分布。在这一阶段，拉应力沿试件长度的受荷方向基本均匀分布。点B和点C之间混凝土微裂缝开始合并形成宏观裂缝，并且拉应变沿试件受荷方向不再均匀分布。当达到峰值荷载（点C）时，一条稳定发展的裂缝便产生了。随着加载的进行，该裂缝区域成为仅存的裂缝发展区域。在峰值荷载处，形成一个条带区，被称为断裂区。超过峰值荷载后，断裂区的拉应变继续增加，而断裂区之外的材料则开始卸载。因此，断裂区的应力-位移关系可通过从总位移中减去弹性位移而得到。因此，受拉混凝土的特性可考虑由两种特征曲线描述：达到峰值荷载前的应力-应变曲线和达到峰值荷载后的应力-位移曲线，如图3.9所示。

(www.xing528.com)

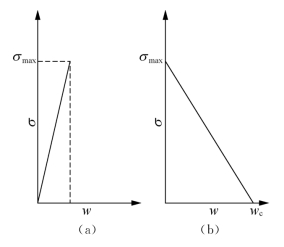
图3.9　（a）峰值前应力-应变关系；（b）峰值后应力-位移关系

一个初始长度为l的混凝土拉伸试件，经历荷载极值之后，试件的伸长量Δl由下式计算：

如果ε0表示断裂区外材料的均匀应变，w表示断裂区的长度增量，那么平均应变εm由下式计算：

由于w相对稳定，表现为混凝土材料的一种固有属性，从式（3.2）可以看到，超过峰值应变之后，平均应变取决于试件的长度。因此，平均应力-应变曲线不再是材料的固有特征。这种现象被称为应变局域化效应（Gdoutos，2005）。