J积分破坏准则在《混凝土断裂力学》中的研究结果

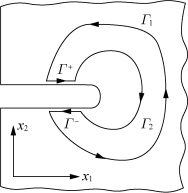
图2.24　J积分的定义

1.J积分的定义

Rice（1968a，b）提出了一种与路径无关的环路积分方法，用于裂缝扩展的分析，称之为J积分。如图2.24所示，考虑裂缝尖端附近任意逆时针回路Γ=Γ1＋Γ＋＋Γ2＋Γ－，则J积分由下式给出：

式中，U是应变能密度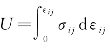，；Tx和Ty分别为路径Γ上的应力分量；ux和uy分别为路径Γ上的位移分量；d s是沿回路Γ的长度增量。

假设裂缝扩展使得裂缝尖端向前移动了一个微小距离d a，这使得围道Γ也随之平动d a，则围道Γ表面应力所做的功（单位板厚）为

由于仅仅朝着裂缝尖端正前方平动，故d x=－d a，d y=0，因此可得：

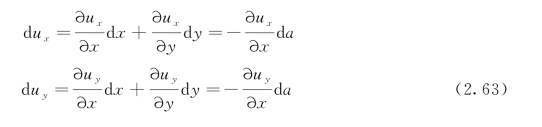
则式（2.62）可修正为

围道平动时，右侧进入的体积将流入应变能，而左侧退出的体积则流出应变能，因而围道平动时其所围域内势能变化为

因此，J积分的含义是当裂缝扩展单位长度时，每单位厚度流入围道Γ的能量。在弹塑性断裂力学中，J积分具有很重要的作用。它避开了直接计算裂缝尖端附近的弹塑性应力场，而用J积分表示裂缝尖端应变集中特征的平均参量，并且被证明：①J积分具有与积分路径无关的属性；②J积分可作为起裂的弹塑性断裂准则：J=JIC，其中JIC为临界值。

2.积分路径无关性

设有包围不含裂缝尖端耗散区的面积Q的任一闭合围道Γ。格林公式指出，函数u（x，y）和v（x，y）有以下关系：

因为，

所以，

根据卡氏定理：(www.xing528.com)

对应变能密度微分，则有：

将式（2.70）代入式（2.68），可见积分号里面的被积函数等于零。因此，对于在不含裂缝尖端耗散区的围道Γ有：

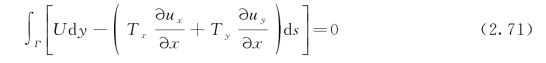
如图2.24所示，先从裂缝下表面按逆时针方向沿Γ1到上表面Γ＋，再由上表面Γ＋到与Γ2的交点，再按顺时针方向沿Γ2回到下表面Γ－，最后回到与Γ1的交点，从而得到封闭曲线Γ，在Γ内没有裂缝尖端的耗散区，于是有：

在Γ＋到Γ－上，即裂缝的上、下表面上，有Tx=Ty=0，且d y=0，所以式（2.72）中后两项积分约为零，于是简化为

这里Γ2的积分路径是按顺时针方向进行。当将Γ2的积分路径也按逆时针方向进行时，就有：

由于Γ1到Γ2是围绕裂缝端部的任意曲线，这就证明了J积分与积分路径的无关性。

3.J积分与能量释放率G和应力强度因子K的关系

由于J积分不依赖于路径，所以在线弹性条件下，裂缝尖端没有塑性耗散区。由于切口是表面自由的，在切口表面上应为零，于是有

可见在线弹性范围内，J积分就是线弹性能量释放率G，因而可以认为J积分就是裂缝扩展单位长度时每单位厚度流向裂缝尖端的能量。已有学者证明，在小范围屈服条件下，J积分依然等于线弹性能量释放率G。

设Q为二维裂缝体的截面，而Γ为其边界曲线，则每单位厚度的势能为

式中，Γt是有牵引力的那部分边界。一般来说，一个力场的势能是物体到零位置（势能为零的位置）过程中该场的力所做的功。所以，牵引力势能也就等于牵引力Tx和Ty通过位移－ux和－uy到零位置过程中所做的功。势能的降低－d V等于流向裂缝尖端的能量J d a，于是有：

所以，J积分也就是裂缝面积的势能减少率。因此，在小范围屈服条件下，J积分等于线弹性能量释放率G。对于弹塑性材料，只要不出现卸载，J积分仍然等于。可见，J积分是线弹性能量释放率的一种推广。

由于塑性变形具有不可逆性，所以将一般弹塑性问题当作非线性弹性问题处理时不允许卸载。但在裂缝扩展过程中，新裂缝面附近的应力总在不断松弛，发生卸载。因此，大范围屈服时式（2.77）将不再适用。