混凝土断裂力学：裂纹尖端塑性区的研究成果

金属材料裂缝尖端会形成塑性区，裂缝扩展所需要克服的塑性功在量级上可高达断裂表面能的三个数量级。因此，裂缝尖端塑性流变为抗裂的主要因素，线弹性断裂力学的方法在一定程度上失效。如前所述，弹塑性断裂力学中，目前应用最广泛的是裂缝尖端张开位移（COD）理论和J积分理论（Rice，1968a，b）。

COD和J积分的临界值给出了近乎与尺寸无关的断裂韧度度量方法，即使对具有较大范围的裂缝尖端塑性区的情况也同样适用。然而，COD和J积分准则仍具有局限性，但它们的局限性远小于线弹性断裂力学（Anderson，2005）。

1.Irwin理论（小范围屈服）

Irwin提出了裂缝尖端塑性区大小的理论。根据式（2.14），无限平板平面应力状态下Ⅰ型裂缝尖端的三个主应力为

Von Mises屈服应力为

由线弹性下的应力场分布可知，对于σs≥fy的范围，必定处于屈服状态。因此，根据式（2.37）和式（2.38），对于平面应力，容易得到该屈服范围的边界曲线方程为

边界曲线形状如图2.15中实线所示，在裂缝尖端的正前方，塑性区尺寸为

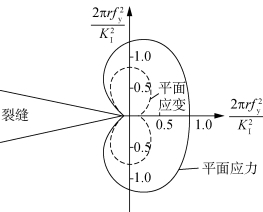
图2.15　裂缝尖端塑性区形状

裂缝正前方的应力分布表达式为

式（2.39）和式（2.40）的塑性区范围只是裂缝尖端线弹性解屈服的范围，实际上由于该区域屈服，将形成所谓的松弛效应，在一定程度上改变了裂缝尖端应力场。

如图2.16所示，虚线AB代表线弹性解下的理想应力分布，考虑屈服导致应力场重新调整后，应力分布将如图中实线CEF所示。假设弹性区内应力积分不变，即曲线EF下的面积等于曲线DB下的面积。对于许多金属材料，这个假定的有效性与试验测得的结果是相符合的。同时，由于线弹性应力场和弹塑性应力场的总应变能维持相等，可推断出曲线AD下的面积等于CE下的面积，故：

图2.16　塑性变形引起的应力松弛效应

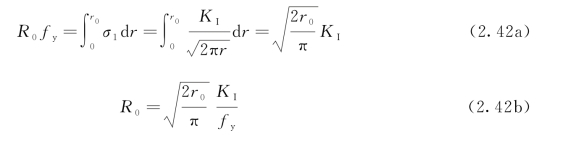
根据式（2.41），有，代入式（2.42b）得到：

由式（2.43）可知，考虑应力松弛效应，塑性区尺寸将增加1倍。以上讨论为平面应力状态，在平面应变状态下，第三个主应力不为0，由下式给出：

将式（2.44）代入式（2.38），得到屈服区的边界曲线方程为

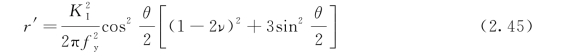
在裂缝尖端的正前方，塑性区尺寸为

同理可得，考虑应力松弛后塑性区尺寸为

其形状如图2.16中的虚线所示。可见平面应变状态下的塑性区比平面应力状态下的塑性区显著缩小了。

需要指出的是，在平面应变状态下，三轴屈服应力fY实际上显著超过单轴屈服应力fy。假设，则可以得到：

由上述讨论可知，Irwin在推导过程中采用了裂缝尖端的单参数K表达近似解，故只在K控制区的范围内才具有可以接受的误差，如果屈服范围超出K控制区，则推导结果应当视为失效。因此，Irwin塑性区范围的理论必须要求屈服范围在K控制区范围内，满足这种情况即可称为小范围屈服。(www.xing528.com)

平面应力状态下的屈服区域较大，小范围屈服应当满足：

平面应变状态下的屈服区域较小，按照式（2.48），则小范围屈服应当满足：

2.Dugdale-Barenblatt理论（大范围屈服）

对于一些韧性好、受荷载比较大的材料，其裂缝尖端不再满足小范围屈服的条件，裂缝尖端的行为已经超出了K控制区，属于大范围屈服的情况。图2.17象征性地表明了这些情况，为方便起见，图中K控制区和塑性区都象征性地绘制为圆。图2.17（a）的塑性区在K控制区以内，故把材料当成理想线弹性体计算得到的弹性应力场的强度因子K，仍然控制着塑性区中的形变和断裂，Irwin理论适用。图2.17（b）中所示的塑性区则已经超出了K控制区，故属于大范围屈服的情况，Irwin理论不再适用。

Irwin关于塑性区大小的修正模型是对LEFM模型相对粗略的改进。而Dugdale-Barenblatt则发展了条带（strip-yield）模型，考虑了更为精确的改进，并得出了封闭解。这一理论（D－B理论）随后促进了内聚区模型的发展，是弹塑性断裂力学中的一个经典例子。

图2.17　小范围屈服和大范围屈服示意图

如图2.18（a）所示，小范围屈服塑性区理论解呈扩散型。1960年，Dugdale通过对软钢薄板裂缝尖端塑性区的试验结果发现，当薄壁容器管道有穿透壁厚的裂缝时，其裂尖的塑性区是狭长块状（图2.19）。在对裂缝尖端塑性区的实际观测中，大范围屈服情况下塑性区的确往往呈现条带型，如图2.18（b）所示。Rice和Druker曾证明，在Tresca屈服条件和平面应力状态下，屈服区确为带状。Dugdale据此建立了裂缝尖端的条带塑性区模型，被称为Dugdale模型。

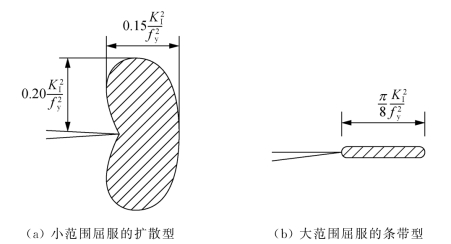
图2.18　裂缝尖端塑性区形状示意图

图2.19　管道轴向裂缝的尖端塑性区　　　

图2.20　Dugdale模型计算示意图

设材料为理想弹塑性，则在沿裂缝扩展方向的屈服带内的应力可取作屈服应力fy（单轴拉伸情况下的屈服应力，讨论平面应力状态）。在屈服区内，解除位移约束，代之以上、下表面之间的作用力fy，如图2.20所示，求解结果必须满足屈服区内位移连续的条件。

将x=a处的裂缝尖端称为物理裂缝尖端。塑性带的出现可以等效为将裂缝尖端向前运动了距离l，屈服应力fy施加在a≤|x|≤a＋l范围内，x=±（a＋l）处称为虚拟裂缝尖端。Dugdale假设，在带状塑性区的虚拟裂缝尖端，由于应力并不存在奇异性，在顶端处总的应力强度因子为零，如图2.21所示。利用这一假设，可以求解带状塑性区的长度。

前文已经给出无限大板中的Grifitth裂缝的应力强度因子，故有：

在裂缝两端长度为l的范围内作用均匀应力fy时对应的应力强度因子为

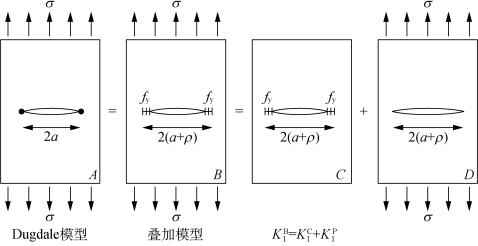
图2.21　Dugdale模型的推导原理

根据可得，条带长度为

当σ≪fy（即应力较小）时，将正割函数展开成幂级数，可近似地得到：

与Irwin的解相比，即式（2.38），可得：

可见，其解比Irwin的结果要大一些。Barenblatt则对Dugdale假设进行了改进，可考虑非理想弹塑性的情况，如图2.22所示。

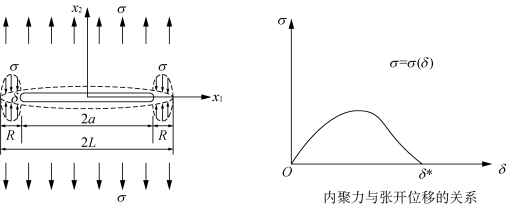
图2.22　Barenblatt内聚力模型