混凝土断裂力学：K控制区边界确定

式（2.14）—式（2.20）实际上是只取Williams级数第一项而得出，可代表应力尖端很小区域范围较精确的近似解，但对于较远端区域，用该略去奇异项的表达式将产生较大误差。以Ⅰ型裂缝正前方为例（即θ=0），由于在对应力应变场分析时略去了r的高次项，所以当式（2.14）中r→∞时，σyy→0，但实际上当r→∞时，σyy→σ。所以，式（2.14）—式（2.20）又称为单参数K表示的裂缝尖端应力应变场，仅适用于裂缝尖端小区域范围的较精确的简洁表达，这个范围即称为K控制区，或者称为K主导区、K场。

通过取Williams级数的前几项，即考虑展开式的奇异项，可以得到精确表达式为

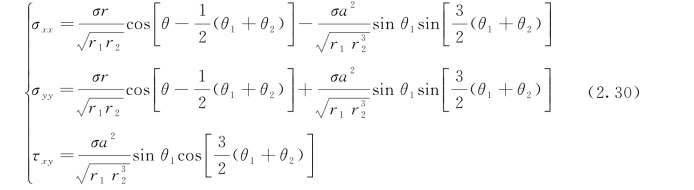
对于裂缝尖端正前方，取θ1=θ2=θ=0，则有：

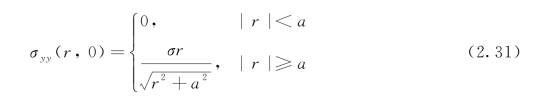
式（2.30）中表达式参数的含义可参见图2.13。当式（2.31）中r→∞时，σyy→σ，因此式（2.31）给出的是无限大板上任意一点的精准应力分量。因此，此解称为全解。

近似解和精确解的误差由下式给出：(https://www.xing528.com)

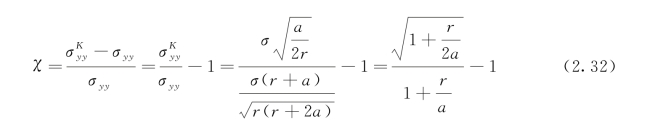
式（2.32）为无限大板的近似解和精确解的误差，同样可以得到类似的三点弯曲试件和紧凑拉伸试件的近似解和精确解的误差，这三种情况下误差百分数随参数r/a的关系如图2.14所示。

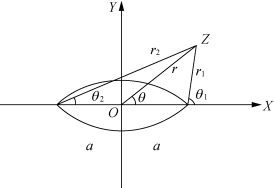
图2.13　应力场精确解中符号的含义　　

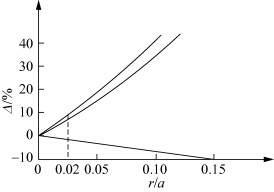
图2.14　近似解和全解的误差

从图2.14可见，当r/a≤0.02时，含中心裂缝无限平板、三点弯曲试件、紧凑拉伸试件三种情况的近似解和精确解的误差分别为－1.5%，6%和7%。因此，工程上通常取r/a≤0.02，能保证三点弯曲试件和紧凑拉伸试件用K来描述其线弹性材料的应力应变场时，精度可在93%以上。因此，r/a≤0.02可作为线弹性材料K控制区的边界。