应力强度因子是线弹性断裂力学里面一个十分重要的概念。Inglis（1913）的研究表明，裂缝尖端附近的应力场具有奇异性。基于已有的数学原理（Westergaard，1939），一系列线弹性裂缝应力场理论得到了发展（Irwin，1957）。研究发现，裂缝尖端附近的应力与裂缝尖端半径r的平方根成比例地减小（r≪a，a为裂缝长度）。在开裂体中，该奇异性独立于边界条件、几何形状及荷载。
图2.6 极坐标表示的Ⅰ型裂缝尖端的应力场
两端受均匀应力的无限宽板的Ⅰ型裂缝尖端附近的应力和位移如图2.6所示（Irwin，1957），由式（2.14）和式（2.15）给出（Irwin，1957）。采用以原点位于裂缝尖端的极坐标，其中半径坐标为r，角坐标为θ，ν为泊松比。
Ⅰ型裂缝尖端应力场：
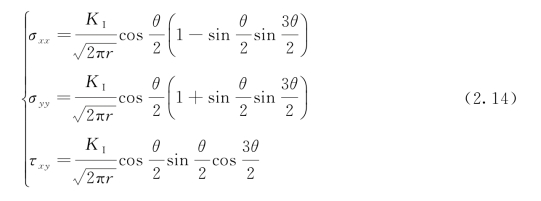
Ⅰ型裂缝尖端位移场：
KI称为Ⅰ型裂缝的应力强度因子（Shear Intencity Factor，SIF）。同样可以写出Ⅱ型和Ⅲ型破坏条件下的应力和位移的类似表达式，它们的应力强度因子分别用KII和KIII表示。
Ⅱ型裂缝为无限宽板，无限远处受平面内的剪切力作用（图2.7）。Ⅱ型裂缝尖端应力场：
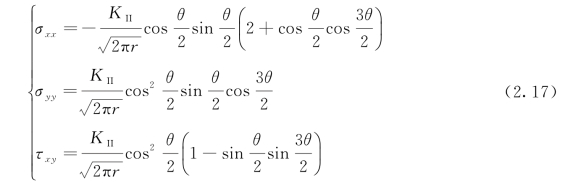
Ⅱ型裂缝尖端位移场：
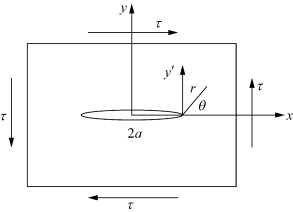
图2.7 Ⅱ型裂缝受力条件
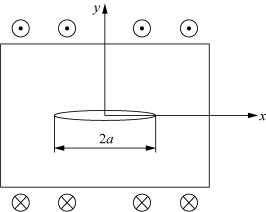
图2.8 Ⅲ型裂缝受力条件
Ⅲ型裂缝为无限宽板，无限远处受与平面方向垂直的剪切力作用（图2.8）。Ⅲ型裂缝尖端应力场：(www.xing528.com)
Ⅲ型裂缝尖端位移场：
上述三种裂缝应力场和位移场表达式，虽然是根据含有裂缝的无限宽板在均布应力条件下获得，但有研究表明，这些解具有普遍性。也就是说，对于其他有限尺寸板的裂缝，在非均匀受力条件下，裂缝尖端附近的应力场表达式是相同的。其不同之处在于，应力场强度因子和结构形状、荷载、边界条件相关联。
需要指出的是，“应力强度因子”与“应力集中系数”两者完全不同，后者用于表征几何不连续处实际应力与平均（或名义）应力之间的比值，而应力强度因子定义了裂缝尖端奇异性的程度，裂缝尖端区域的应力场奇异程度与应力强度因子成正比。当构件受到拉应力或弯曲应力时，弹性条件下裂缝尖端附近的应力场表现出奇异性，并与到裂缝尖端距离的平方根成反比。总而言之，应力强度因子描述了奇异性的程度。
由于裂缝尖端附近的应力场和位移场都由应力强度因子控制，所以可以进一步假设，对于任意破坏类型，裂缝尖端的临界应力可以用临界应力强度因子来定义。因此，可以使用单一参数即应力强度因子来合理地表征线弹性断裂力学的强度概念。
上述三种情况下，应力强度因子分别为
一般都将应力强度因子乘以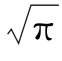
，这样的好处是使以后导出的G与K的关系式较为简洁。对于其他结构和裂缝形态下的应力强度因子，其形式通常需要在式（2.21）上再乘以一个非1的形状系数Y（表2.1）。
表2.1 若干有限宽板应力强度因子K的形状系数Y
举例来说，半无限平面内的边缘裂缝的
（图2.9）；无限宽板内的周期裂缝
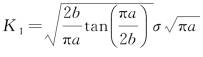（图2.10）；紧凑拉伸试件
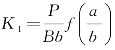（图2.11），其中
。其他一些有限宽板的裂缝尖端应力强度因子形状系数Y如表2.1所示。
图2.9 半无限平面内的边缘裂缝
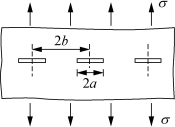
图2.10 无限宽板内的周期裂缝
图2.11 紧凑拉伸试件
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
