混凝土断裂力学-能量释放率

根据晶体材料的理论强度公式：

式中，E为材料弹性模量；γ为表面能密度；β为晶体材料的晶格间距。

按照式（2.2），玻璃的理论强度应该可以达到1 000 MPa以上。这与当时试验得到的强度100 MPa相差极大，令研究人员十分困惑。

Griffith开展的试验还发现，随着玻璃纤维直径减小，断裂应力将增加，强度表现出了尺寸效应。通过试验观察到，小的缺陷对材料性能的损伤作用比大的缺陷小得多。这在理论上让人困惑，因为根据当时所用的断裂判据预测，如果这些缺陷在几何上相似，如图2.3和式（2.1）所示例子，那么这些缺陷引起的应力集中程度应该是一样的，而与缺陷的大小无关。因而按照经典的强度理论，不管缺陷的大小如何，它们对强度的影响应该是一样的，这与试验观察到的结果并不一致。

为了解释缺陷尺寸对宏观断裂强度的影响，Griffith创新性地提出了一种基于能量平衡的方法，这种方法不仅基于外荷载的势能与储存的弹性应变能，而且还基于断裂表面能，用来解释缺陷的尺寸效应。这种断裂表面能与断裂过程中产生的新鲜表面有关。Griffith的方法将图2.3中的椭圆短边设为0，得到Griffith裂缝，如图2.4所示，为方便讨论，此处假设板为单位厚度（即板厚B=1）。

如图2.4（b）所示，对于不同的裂缝长度，在裂缝长度不变的前提下，对于线弹性体，力P和对应的位移Δx成正比关系。当裂缝长度由2a变为2a＋Δa时，系统刚度将降低，位移Δx将变为Δx＋dΔx。由图可知，前后两种情况下弹性体系的应变能增量为0.5PΔx，而该过程中外力所做的功为PΔx。也就是说，外荷载所做的功是应变能增量的2倍。Griffith创新性地认为，与增加的应变能相等的另外一半功将被用于克服裂缝扩展产生的新表面所需的断裂表面能。由于裂缝扩展，在该过程中与结构增加的弹性应变能相等的外力功的一半，将从应变能释放成为新增的断裂表面能。

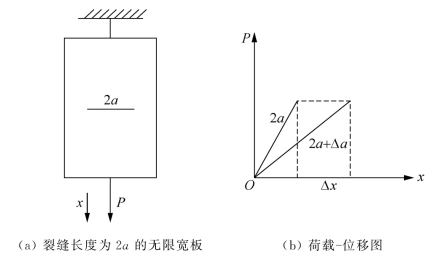
图2.4　Griffith提出的能量释放率概念

裂缝延长过程中，断裂表面能的增量为4aγ（注意，裂缝长度为2a，应包括裂缝的上、下两个表面）。Griffith（1921）采用Inglis（1913）的研究成果并进一步推导得到：两端受均匀应力的平板中一条椭圆形裂缝引起的应变能变化为。因此，外荷载做功为。因裂缝的引入导致系统的能量变化为

根据虚位移原理，当无限板中已经存在裂缝长度2a时，裂缝不会扩展的稳定条件为

即当裂缝扩展单位长度所释放的应变能大于形成新断裂自由表面所需要的断裂能2γ时，该裂缝长度2a所处状态是不稳定的，裂缝将扩展。由式（2.4）可知，如果给定裂缝长度2a，当时，得到裂缝处于扩展的临界应力（平面应力）为

在满足裂缝扩展的前提下，裂缝稳定扩展的条件为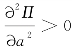，裂缝失稳扩展的条件为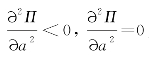则为临界状态。对于本算例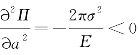，。因此，裂缝如果扩展，总是不稳定的扩展，即一旦裂缝扩展，将导致裂缝贯穿无限平板。因此，式（2.5）即为有缺陷情况下的宏观抗拉强度。

式（2.5）意义重大，因为它将缺陷尺寸2a与材料的抗拉强度联系起来。它预测小的缺陷比大的缺陷对材料的损伤作用要小，这与试验观察到的结果一致。Griffith的工作为线弹性断裂力学的创立和发展开拓了道路，尽管他的工作最初也被忽视了许多年。

Griffith提出的断裂能实际上为克服分子键所需要的能量，而非仅仅热力学意义上的表面能。因此，Irwin提出应该测定材料在断裂试验中的特征表面能，而不是使用热力学表面能。他引入Gc变量作为增加单位裂缝面积所需要做的功，也称为临界能量释放率。Gc一般可采用形状简单的试件通过试验来确定。一旦材料的Gc值已知，假定它是一种材料性能，通过一定的方法可以确定一条给定的裂缝在任何其他加载条件下会不会扩展。这个方法的过程很简单：计算每增加单位面积的裂缝所释放的能量G，如果这个能量释放率低于临界能量释放率G<Gc，则裂缝不会扩展；相反，如果G>Gc，则裂缝会扩展。对于能量释放率与临界能量释放率相等的特殊情形G=Gc，裂缝处于临界的平衡状态。

以上为方便分析得到简单的解析解[式（2.5）]，假设无限板两端受均布应力作用，当假定临界能量释放率Gc作为材料的一种固定属性时，则与外荷载的形式无关。因此，为了计算和测试Gc，则无须采用均布应力。为方便起见，采用一个集中力，说明如何计算Gc值。依然考虑图2.4所示的平板，板厚度为B，这时可用裂缝长度的增加量Δa来得到释放的能量：

(www.xing528.com)

式中，ΔUe是裂缝长度增加Δa所引起的弹性应变能变化，以微分的形式可表达为

引入柔度，则应变能Ue为

得到：

因此，对于一个给定的试件形状，当柔度与裂缝长度的关系已经获得时，临界能量释放率Gc可通过记录断裂时的荷载确定。

【例2.1】　计算如图2.5所示的双悬臂梁的能量释放率。另外，分析在荷载控制和位移控制条件下裂缝在其自身平面内的稳定性。忽略剪切挠度。

图2.5　算例

采用简支梁理论容易得到每根悬臂梁的挠度：

式中，E为弹性模量；I为惯性矩，。

因此，柔度由下式给出：

能量释放率为

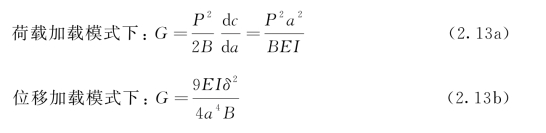
在荷载控制条件下，有，因此在荷载控制条件下，随着裂缝的扩展，能量释放率在增加，裂缝将失稳扩展。

在位移控制条件下，有，因此在位移控制条件下，随着裂缝的扩展，能量释放率在降低，裂缝将稳定扩展。