裂缝的基本形态可分为张开型、划开型和撕开型三种（图2.1），裂缝的扩展也可能是这三种形态的复合模式。
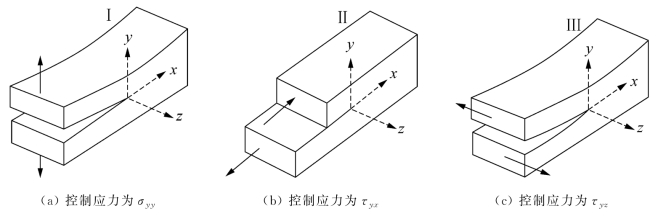
图2.1 裂缝的三种基本形态：（a）Ⅰ型（张开型）；（b）Ⅱ型（滑开型，或面内剪切型）；（c）Ⅲ型（撕开型，或反平面剪切型）
线弹性断裂力学（Linear Elastic Fracture Mecachins，LEFM）研究理想脆性材料裂缝尖端材料行为、扩展准则和规律，其发展起源可以追溯到20世纪初。当时，Inglis（图2.2）发表了一项在外边界加载的无限长线弹性板中的椭圆形孔应力分析的开创性研究工作，模拟了类似裂缝的非连续性，通过使短轴远小于长轴，可在裂缝尖端观察到应力奇异点（即无限应力集中）。之后，Griffith（1921）提出了一种基于能量准则的新方法，至此，这一领域的研究得以正式发展。从那时起，又经过了四十多年的时间，Irwin（1957）提出“应力强度因子”的概念后，线弹性断裂力学这门学科正式诞生。
1913年，Inglis发表了基于弹性力学分析得到的一个两端受均匀应力且含有椭圆形孔的薄板（即平面应力问题）的位移场和应力场解析解。由于假设椭圆孔相对于薄板尺寸可以忽略，因此可以认为薄板为无限大（图2.3）。Inglis根据之前的研究得出，最大应力将发生在椭圆的A点，其大小为
(www.xing528.com)
图2.2 Inglis
根据该结果，可以知道，椭圆的A点将存在应力集中现象，而应力集中的程度和椭圆的两个主轴长度比成正比关系。当b趋向于无穷小时，A点应力将趋向于无穷大；而当a趋向于无穷小时，该微小椭圆孔对无限板的应力不产生任何影响。可见，当a趋向于无穷小时，A点的应力存在奇异现象。而裂缝尖端的力学行为与这种情况有类似之处。
图2.3 无限宽板中的椭圆形孔
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
