多元回归分析及预测模型解释

多元统计方法包括多元回归分析、逐步回归分析。多元分析方法具有很严密的数学推理，自然也必须在满足其苛刻的应用条件（即各因素之间不相关、因素与目标线性强相关）的前提下才能得出较好的结果。但是，在实际评价过程中，往往已知样本的取得已经是非常困难的一件事，更为糟糕的是形成的已知样本常常通不过假设检验。因此这种方法在鲁棒性上较神经网络、模糊综合评判要差一些，其应用也相应受到一定的限制。下面对多元线性回归的原理作一阐述。

（1）线性回归方程的建立。设变量y与变量χ1，χ2，…，χp有关，则其p元线性回归模型为

其中，ε是随机误差。对y及χ1，χ2，…，χp作n次抽样得到n组数据：

其中，ya为样本值，εa为遵从正态分布N（0，σ2）的n个相互独立同分布的随机变量，a=1，2，…，n。于是有

设b0，b1，…，bp分别为参数β0，β1，…，βp的估计值，则得回归方程：

式中 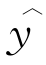——回归值。(www.xing528.com)

ya-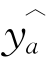（a=1，2，…，n）为残差，它刻画了样本值与回归值的偏差。

根据最小二乘法使残差平方和达到最小的原理，即

根据微积分极值原理，b0，b1，…，bp必须满足：

解出b1，b2，…，bp，并解出b0代入即得多元回归方程。

（2）回归方程的预测和外推。在使用回归方程前，必须对回归方程和回归系数进行检查，如果通过了显著性检查，就可以进行回归方程的预测和外推。在预测区，划分出评价预测单元（共k个），选出评价因素p个，利用已建立的回归方程可进行预测，将评价单元i的各评价因素代入回归方程，得到用作为y（i）的估计。