模糊综合评判在公路地质灾害危险性评价中的应用

模糊综合评判就是以模糊数学为基础，应用模糊变换原理的最大隶属度原则，考虑与被评判事物相关的各个因素，对其所做的综合评判。由于在很多问题上，人们对事物的评价常常带有模糊性，因此，应有模糊学的方法进行综合评判将会取得很好的实际效果。

如果评判对象的有关因素很多，很难合理的定出权重数分配，即难以真实地反映各因素在整体中的地位，这是采用多级综合评判。

设因素集U={u1，u2，…，um}。

设危险性等级集V={v1，v2，…，vn}。

评价因素和危险性等级之间的模糊关系用矩阵来表示：

其中，rij=μ（ui，vj）（0≤rij≤1），表示就因素ui而言被评为vj的隶属度；矩阵中第i行Ri=（ri1，ri2，…rin）为第i个评价因素ui的单因素评判，它是V上的模糊子集。

实际上，不同因素在地质灾害危险性评价中所起的作用是有大小之分的，即必须考虑因素的权重问题。(www.xing528.com)

假定a1，a2，…，am分别是评价因素{u1，u2，…，um}的权重，并满足a1+a2+…+am=1，令=（a1，a2，…，am），则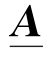为反映因素权重的模糊集（即权向量）。

由权向量与模糊矩阵进行“合成”得到综合隶属度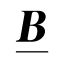，即通过模糊运算求出模糊集B=（b1，b2，…，bn）（0≤bj≤1），其中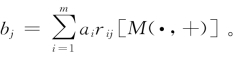

根据最大隶属度准则，所对应的分级即为危险性等级i0。

在实际运用模糊综合评判的过程中，常常首先遵循地质和灾害发生的规律，将评价目标分划为几个子目标，每个子目标又对应数个评价因素指标，对每个子目标进行模糊综合评判，然后再以子目标为评价因素，以对评价总目标进行模糊综合评判，称之为两级模糊综合评判。

国内已有不少成功运用两级模糊综合评判的例子，两级模糊综合评判最大的好处在于分层次评价与人脑通常的思维方式吻合，特别是各个子目标下的因素指标相对较少、便于比较，这样便大幅度降低了确定权重和隶属度的难度。然而子目标的分划常常也不是件很容易的事情，何况往往无法保证各子目标所对应的因素指标完全独立。

两级模糊综合评判的数学原理和方法与一级模糊综合评判完全相同，此处不再赘述。