回旋线：道路工程中的缓和曲线

（一）回旋线的数学表达式

回旋线是公路路线设计中最常用的一种线型。我国《标准》规定缓和曲线采用回旋线。其基本公式为

式中　r——回旋线上某点的曲率半径，m；

　　　l——回旋线上某点到原点的曲线长，m；

　　　A——回旋线的参数。

由于rl的单位是长度的二次方（m2），为使量纲一致，故令C＝A2，A表征回旋线曲率变化的急缓程度。在回旋线的任一点上，r是随l的变化而变化的，但在缓和曲线的终点处，l＝Ls，r＝R，则上式可写作

则参数

式中　R——回旋线所连接的圆曲线半径；

　　　Ls——回旋线型的缓和曲线长度。

设计上可以由已知R和Ls计算A，也可以按各种条件选择R和A，再计算Ls。

图4-12为回旋线及其应用范围。

如图4-12所示，在回旋线上任一点P取微分单元，则有

以r·l＝A2代入，得

当l＝0，β＝0，l·dl＝A2·dβ

积分得：

以rl＝A2代入，得

再代入式（4-21）、式（4-22），得

将上式积分并将sinβ、cosβ用级数展开整理，即得用参数r和l表示的回旋线直角坐标方程：

在回旋线终点处，l＝Ls，r＝R，于是

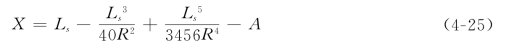
用切线支距法敷设回旋线，采用以下近似公式：

式中，l为任意点的弧长；C＝RLs，R是圆曲线半径；Ls是缓和曲线长度。应用上，上述长度单位均以m计。

图4-12　回旋线

图4-13　回旋线要素

（二）回旋线的几何要素

1.各要素的计算公式

如图4-13所示，任意点P处的曲率半径为(www.xing528.com)

P点的回旋线长为

上二式中的β是回旋线上任一点P的切线方向与x轴的夹角，称作“缓和曲线角”。其值为

P点曲率圆的内移值为

P点曲率圆的圆心M点的坐标为

长切线长为

短切线长为

P点的弦长为

P点的弦偏角为

2.有缓和曲线的道路平曲线几何要素

如图4-14所示，道路平面线形三要素的基本组成是：直线—回旋线—圆曲线—回旋线—直线。计算公式为

用切线支距法敷设回旋线的公式如式（4-24）。用切线支距法敷设带有回旋线的圆曲线公式为

图4-14　“基本型”平曲线

式中　lm——圆曲线商任一点m至缓和曲线终点的弧长，m；

　　　αm——lm所对应的圆心角，rad。

公式的推导和详细敷设方法参见《测量学》。

【例4-1】已知某弯道交点JD5的桩号为K4＋099.51，R＝200m，转角α＝30°04′。试计算曲线要素和主点桩号。

解1.曲线要素计算

2.主点桩号计算

校核：QZK4＋098.27＋J/2＝K4＋099.51（JD）

校和无误。

【例4-2】　已知某弯道JD6的桩号为K4＋650.56，R＝300，ls＝60m，α＝35°00′。试计算曲线要素及主点桩号。

解1.曲线要素计算

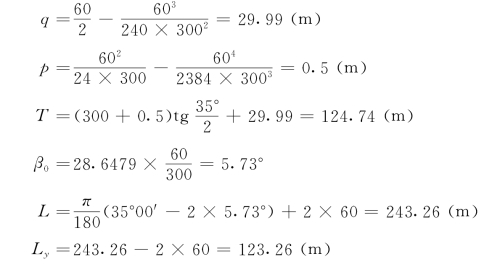
2.主点桩号计算