路段超高缓和段或超高过渡段的规定及要求

（一）超高及其作用

为抵消车辆在曲线路段上行驶时所产生的离心力，将路面做成外侧高于内侧的单向横坡的形式，这就是曲线上的超高。合理地设置超高，可以全部或部分抵消离心力，提高汽车行驶在曲线上的稳定性与舒适性。当汽车等速行驶时，圆曲线上所产生的离心力是常数，而在回旋线上行驶则因回旋线曲率是变化的，其离心力也是变化的。因此，超高横坡度在圆曲线上应是与圆曲线半径相适应的全超高，在缓和曲线上应是逐渐变化的超高。这段从直线上的双向横坡渐变到圆曲线上的单向横坡的路段，称作超高缓和段或超高过渡段。四级公路不设回旋线，但曲线上若设置有超高，从构造的角度也应有超高缓和段。

各级道路圆曲线部分最大超高值规定见表3-14和表3-15。超高值的大小与计算行车速度、半径、路面类型、当地的自然条件等因素有关，设计时可参照《规范》。

表3-14　公路最大超高值

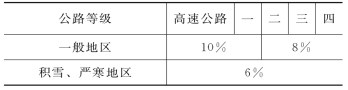
表3-15　城市道路最大超高值

高速公路、一级公路的超高横坡度不应大于10%，其他各级公路不应大于8%，积雪冰冻地区，最大超高横坡度不宜大于6%。当超高横坡度的计算值小于路拱坡度时，应设置等于路拱坡度的超高。因此，各级公路和城市道路圆曲线部分的最小超高值是该道路直线部分的路拱坡度之值。此外，当圆曲线半径很大时，则可不设超高，这时的曲线路段与直线路段一样，做成双向倾斜的路拱。

（二）超高的过渡

1.无中间带道路的超高过渡

无中间带的道路行车道，无论是双车道还是单车道，在直线路段的横断面均为以中线为脊向两侧倾斜的路拱。路面要由双向倾斜的路拱形式过渡到具有超高的单向倾斜的超高形式，外侧须逐渐抬高，在抬高过程中，行车道外侧是绕中线旋转的，若超高横坡度等于路拱坡度，则直至与内侧横坡相等为止，如图3-19所示。

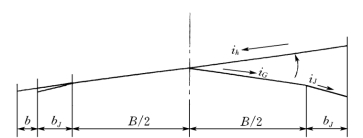
图3-19　超高值等于路拱时的过渡

当超高坡度大于路拱坡度时，可分别采用如下三种过渡方式：

（1）绕未加宽前的内侧车道边缘旋转。先将外侧车道绕路中线旋转，待达到与内侧车道构成单向横坡后，整个断面再绕未加宽前的内侧车道边缘旋转，直至超高横坡值，如图3-20（a）所示。

（2）绕中线旋转，先将外侧车道绕路中线旋转，待达到与内侧车道构成单向横坡后，整个断面绕中线旋转，直至超高横坡度，如图3-20（b）所示。

（3）绕外边缘旋转。先将外侧车道绕外边缘旋转，与此同时，内侧车道随中线的降低而相应降低，待达到单向横坡后，整个断面仍绕外侧车道边缘旋转，直至超高横坡度，如图3-20（c）所示。

图3-20　无中间带道路超高过渡方式

（a）绕内侧边缘旋转；（b）绕中线旋转；（c）绕外侧边缘旋转

上述各种方法中，绕边线旋转，由于行车道内侧不降低，有利于路基纵向排水，一般新建工程多用此法。绕中线旋转可保持中线标高不变，且在超高坡度一定的情况下，外侧边缘的抬高值较小，多用于旧路改建工程。而绕外侧边线旋转是一种比较特殊的设计，仅用于某些为改善路容的地点。

2.有中间带公路的超高过渡

（1）绕中间带的中心线旋转。先将外侧行车道绕中间带的中心旋转，待达到与内侧行车道构成单向横坡后，整个断面一同绕中心线旋转，直至超高横坡度值。此时中央分隔带呈倾斜状，如图3-21（a）所示。

图3-21　有中间带道路超高的过渡方式

（a）绕中间带的中心线旋转；（b）绕中央分隔带边缘旋转；（c）绕各自行车道中线旋转

（2）绕中央分隔带边缘旋转。将两侧行车道分别绕中央分隔带边缘旋转，使之各自成为独立的单向超高断面。此时中央分隔带维持原水平状态，如图3-21（b）所示。

（3）绕各自行车道中线旋转。将两侧行车道分别绕各自的中心线旋转，使之各自成为独立的单向超高断面。此时中央分隔带两边缘分别升高与降低而成为倾斜断面，如图3-21（c）所示。

三种方式的优缺点与无中间带的公路相似。中间带宽度较窄的（≤4.5m）可采用（1）法；各种中间带宽度的都可以用（2）法；对于车道数大于4条的公路可采用（3）法。城市道路的超高过渡方式与公路相同。分离式断面的道路由于上、下行车道是各自独立的，其超高的设置及其过渡可按两条无分隔带的道路分别予以处理。

（三）超高缓和段长度

为了行车的舒适、路容的美观和排水的通畅，必须设置一定长度的超高缓和段，超高的过渡则是在超高缓和段全长范围内进行的，双车道公路超高缓和段长按式3-24计算：

式中　Lc——超高缓和段长，m；

　　　β——旋转轴至行车道（设路缘带时为路缘带）外侧边缘宽度，m；

　　　Δi——超高坡度与路拱坡度的代数差，%；

　　　p——超高渐变率，即旋转轴线与行车道（设路缘带时为路缘带）外侧边缘线之间的相对坡度，其值可按表3-16确定。

表3-16　超高渐变率

根据式（3-24）计算的超高缓和段长度应凑成5m的整倍数，并不小于10m的长度。多车道公路的超高缓和段长度，视车道数按上式计算之值乘以下列系数：

从旋转轴至行车带边缘的距离　系数

　　　　　　　2车道　　　　1.5

　　　　　　　3车道　　　　2.0

因为在确定缓和曲线长度时已经考虑了超高缓和段的长度，所以在一般情况下超高缓和段的长度与缓和曲线的长度相等。但有时为照顾线形的协调性，在平曲线中配置了较长的回旋线，则超高的过渡可仅在回旋线某一区段内进行。因为过小的渐变率对路面排水不利。从利于排除路面降水考虑，横坡度由2%（或1.5%）过渡到0%路段的超高渐变率不得小于1/330。

四级公路可不设缓和曲线，但圆曲线上如有超高，则应设置超高缓和段。超高的过渡在超高缓和段的全长上进行。超高加宽示意图如图3-22所示。

图3-22　平曲线上路面的超高加宽示意图

（a）超高加宽示意图；（b）超高加宽平面图

（四）横断面上超高值的计算

在公路工程施工中，路面的超高横坡即正常路拱横坡是不便于用坡度值来控制，而是用路中线及路基、路面边缘相对于路基设计高程的相对高差来控制的。因此，在设计中为便于施工，应计算出路线上任意位置的路基设计高程与路肩及路中线的高差。所谓超高值就是指设置超高后路中线、路面边缘及路肩边缘对路基设计高程的高差。

图3-23　正常断面超高值计算图

路基设计高程一般是指路肩边缘的高程，在设置超高、加宽路段，为未设超高、加宽前的路肩边缘的高程。如图3-23所示。

设路面宽度为b，路肩宽度为a，路拱坡度为i1，路肩横坡为i2，路面加宽值为bj，路面超高坡度为ib，则对于直线段及不设超高、加宽的平曲线段上的标准横断面中，其路中线与设计标高的高差为h中：

而两侧路肩边缘与设计标高的高差为零。

对于设置超高的平曲线段，其路中线及路肩边缘与设计高程的高差（超高值）的计算方法则随超高的旋转方式而异，现分别加以介绍。

1.绕路面边缘旋转的超高值计算

由前面的分析可知，平曲线上路面的超高值随其在平曲线上所处的位置的不同而变化。在超高缓和段上，路面由直线上的正常路拱逐渐变化到圆曲线的超高横坡，而在圆曲线上路面保持这一超高横坡不变。因此，缓和段的路拱形式与坡度大小和圆曲线段都不同，所以就要根据在平曲线上的不同位置，分别计算其相应的超高值。

（1）圆曲线段的全超高断面。圆曲线段全部为超高坡度ib的超高横坡，如图3-24所示。

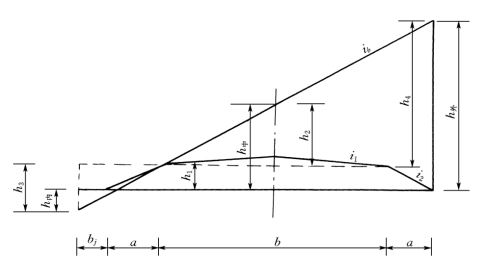
图3-24　全超高断面超高值的计算图

由图3-24可知，h1＝ai2，h2＝，h3＝－（a＋bj）ib（负值表示低于旋转轴），h4＝（a＋b）ib，则

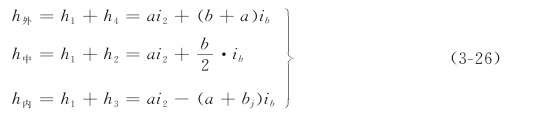
式中　h外——曲线外侧路肩边缘与设计高程之高差，m；

　　　h中——路中线与设计标高程的高差，m；

　　　h内——曲线内侧路肩边缘与设计高程的高差，m；

其余符号意义同前。(www.xing528.com)

上式就是绕路面内边缘旋转的超高的圆曲线段上的超高值的计算公式。圆曲线上任一点的超高值都相等。

（2）超高缓和段上的超高值的计算。按超高设置方法，超高缓和段的渐变是按路面外边缘线相对于设计高程的高差值随离缓和段起点的距离成正比例增加的规律进行的，而路中线及路面外边缘随之也做相应的变化，路肩边缘也就随路面做相应渐变。

由于超高渐变过程是经过三个阶段完成的，而每一阶段的路拱形状都不相同，所以超高缓和段上的超高值就要分阶段分别计算。

①起始断面。在超高缓和段起、终点处，经过提肩，形成路肩与路面相同横坡度的双坡断面，如图3-25所示。由图3-25可看出：

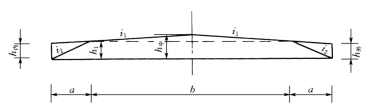
图3-25　起始断面超高值计算

②双坡断面（x≤L1）。设x为超高缓和段上任一点离开缓和段起点的距离，L1为缓和段内双坡断面长度。双坡断面就是指双坡断面内任一点的断面，即从超高缓和段起点至路面外侧变成与内侧相同坡度这一阶段内的断面。如图3-26所示，缓和段上任一点距起点的距离为x，路肩边缘由A升高到C点，则曲线外侧的超高值为AC与提肩高度之和。

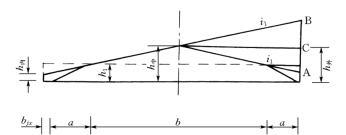
图3-26　双坡断面超高值计算图

C点为超高渐变过程中从起始断面的A点逐渐向双坡阶段终点B过渡过程中的一点，根据超高渐变规律，AC/AB＝x/L1，，其中AB＝2（b/2＋a）i1＝（b＋2a）i1，则

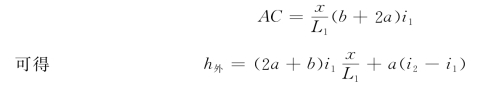
在双坡阶段中，路中线是保持不变的，其超高值为

路面内侧的横坡保持不变，但当路面设置加宽时，路面及路肩边缘则随路面加宽值的渐变而做相应的变化，其超高值为

因此，双坡断面的超高计算公式为

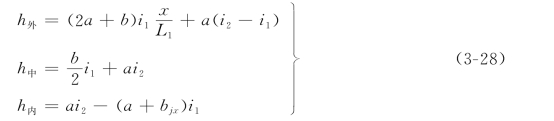
式中　bjx——超高缓和段上任一点的路面加宽值，根据所采用的加宽过渡方式选定相应的计算公式进行计算；

其余符号意义同前。

③旋转断面（x≥L1）。旋转断面是指旋转阶段内的任意断面的路拱情况。

如图3-27所示，设旋转阶段中任一点离开缓和曲线起点的距离为x（x＞L1），其路面横坡度为ix，根据超高渐变规律，在超高缓和段上，超高坡度是由零按直线比例增加到设计超高坡度ib的，故

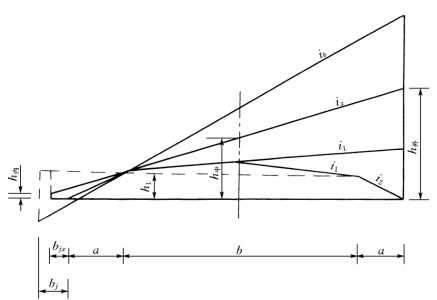
图3-27　旋转断面超高值计算图

但当缓和段较长，L1是按330i1b计算出来时，ix的计算公式应为

根据图3-27得旋转阶段上的超高值计算公式为

式中　bjx——缓和段上任一点的路面加宽值，计算方法同前。

2.绕路中线旋转的超高值计算方法

其计算公式的推导方法同绕路面内边缘旋转的相同，这里不再详细推导，只列出计算公式。

（1）圆曲线段内全超高断面超高值的计算：

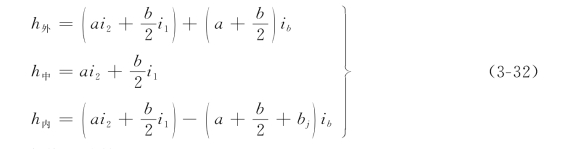
（2）超高缓和段内超高值的计算：

1）起始断面为

2）双坡断面（x≤L1）为

与绕路面内边缘旋转方式同理，若按上式计算的L1值来计算超高渐变率p，则得

若p值小于1/330，则说明L1太长，而应按满足p＝1/330的要求确定：

3）旋转断面（x＞L1）为

若L1是按330i1b计算出来的，则

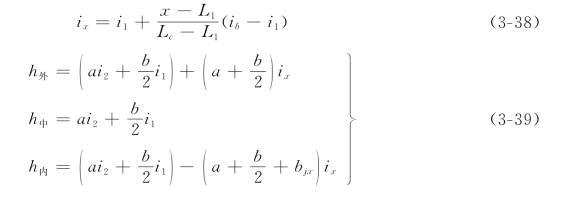
各符号意义同前。

【例3-1】　某平原区四级公路，计算行车速度为40km/h，路基宽度7.0m，路面宽6.0m，路面横坡度3%，路肩横坡4%，有一半径125m的弯道。试计算该弯道圆曲线段，超高缓和段起点以及距离起点15m和30m的超高值（按一般地区考虑，旋转方式为路面内边缘）。

解：

1.确定超高缓和段长度Lc

根据公路等级、自然条件及圆曲线半径可采用的超高横坡度ib＝6%。四级公路绕路面边缘旋转方式的超高渐变率p＝1/100，则可计算出

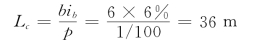
2.确定路面加宽值及加宽缓和段长度

根据公路等级及圆曲线半径查表，按一类加宽选用路面加宽值bj＝0.8m，加宽缓和段长度采用超高缓和段长度，加宽过渡方式按正比例增加方式确定。

3.计算超高值

（1）计算圆曲线段内的超高值。因为路面宽b＝6.0m，路基宽B＝7.0m，因此路肩宽度为a＝0.5m，则得

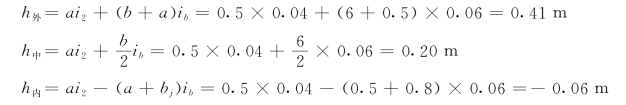
（2）计算超高缓和段起点的超高值。因为超高缓和段起点即为起始断面，则得

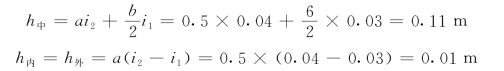
（3）计算距离缓和段起点15m处的超高值。首先应判断该处是在双坡断面还是在旋转断面，为此需计算出双坡阶段长度L1：

因为该点距离起点的距离小于L1，所以该处是在双坡断面上。则

其中×0.8＝0.33 m

（4）计算距离起点30m处的超高值。因为x＝30m，x＞L1，所以该处是在旋转阶段内，这时路面的横坡度ix为