(一)考试要求
1.《考试大纲》的要求:一级掌握,二级了解
2.“试题”回顾:
【试题7.4.1】 预拱度的设置(1998年)
预应力混凝土公路简支梁桥预拱度设置时考虑的因素,以下何项为正确?
(A)恒载影响 (B)预应力影响
(C)活载影响 (D)恒载+预应力+1/2静活载影响(不计冲击力)
【试题7.4.2】 预拱度的设置(2000年)
按全预应力混凝土构件设计的简支梁桥,变形验算时,在活载作用下截面的几何特性应为以下何项所示?(Eh为混凝土弹性模量,I0l为开裂截面换算惯性矩,I0为构件换算截面惯性矩)
(A)Eh·I0 (B)Eh·I01
(C)0.85Eh·I0 (D)0.85Eh·I01
【试题7.4.3】~【试题7.4.4】(2007年)
某单跨预应力钢筋混凝土屋面简支梁,混凝土强度等级为C30,计算跨度l0=17.7m,要求在使用阶段不出现裂缝。
【试题7.4.3】 预应力混凝土构件的刚度
该梁跨中截面按荷载效应的标准组合计算的弯矩值Mk=700kN·m,按荷载效应的准永久组合计算的弯矩值Mq=650kN·m,换算截面惯性矩I0=3.4×1010mm4。试问,该梁按荷载效应标准组合并考虑荷载长期作用影响的刚度B(N·mm2),应与下列何项数值最为接近?
(A)3.85×1014 (B)4.50×1014 (C)5.70×1014 (D)5.82×1014
【试题7.4.4】 预应力混凝土构件的挠度
该梁按荷载短期效应组合并考虑荷载长期作用影响产生的挠度值f1=56.6mm。计算求得的预应力短期反拱值f2=14.2mm;该梁属于在使用上对挠度有较高要求的构件。试问,该梁的挠度值与规范允许的挠度值之比,应与下列何项数值最为接近?
(A)0.59 (B)0.64 (C)0.83 (D)1.28
【试题7.4.5】 预应力混凝土构件的长期刚度(2009年)
某预应力钢筋混凝土受弯构件,截面尺寸为b×h=300mm×550mm,要求不出现裂缝。经计算,跨中最大弯矩截面Mq1=0.8Mk1,左端支座截面Mq左=0.85Mk左,右端支座截面Mq右=0.7Mk右。当用结构力学的方法计算其正常使用极限状态下的挠度时,试问,刚度B按以下何项取用最为合适?
(A)0.47EcI0 (B)0.42EcI0 (C)0.50EcI0 (D)0.72EcI0
(二)《混凝土结构设计规范》规定和算例
《混凝土结构设计规范》规定:
3.4.3 钢筋混凝土受弯构件的最大挠度应按荷载的准永久组合,预应力混凝土受弯构件的最大挠度应按荷载的标准组合,并均应考虑荷载长期作用的影响进行计算,其计算值不应超过表3.4.3规定的挠度限值。
表3.4.3 受弯构件的挠度限值
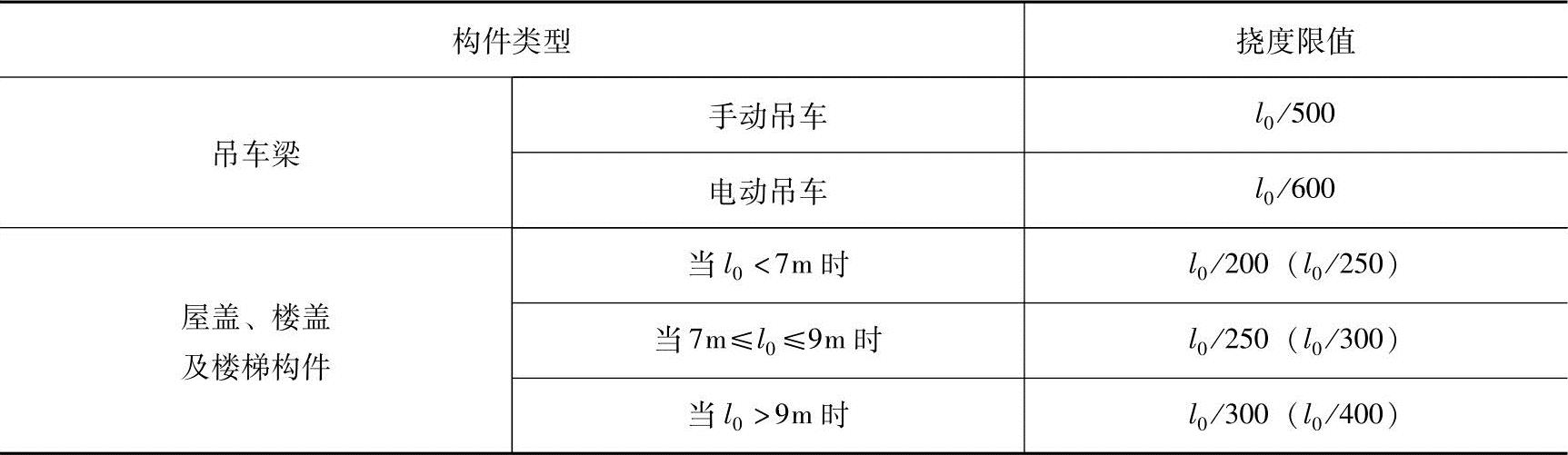
注:1.表中l0为构件的计算跨度;计算悬臂构件的挠度限值时,其计算跨度l0按实际悬臂长度的2倍取用;
2.表中括号内的数值适用于使用上对挠度有较高要求的构件;
3.如果构件制作时预先起拱,且使用上也允许,则在验算挠度时,可将计算所得的挠度值减去起拱值;对预应力混凝土构件,尚可减去预加力所产生的反拱值;
4.构件制作时的起拱值和预加力所产生的反拱值,不宜超过构件在相应荷载组合作用下的计算挠度值。
7.2.3 按裂缝控制等级要求的荷载组合作用下,钢筋混凝土受弯构件和预应力混凝土受弯构件的短期刚度Bs,可按下列公式计算:
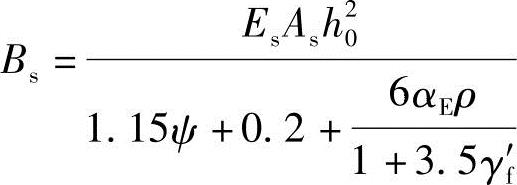
2.预应力混凝土受弯构件
1)要求不出现裂缝的构件
Bs=0.85EcI0 (7.2.3-2)
式中 I0——换算截面惯性矩。
7.2.2 矩形、T形、倒T形和I形截面受弯构件考虑荷载长期作用影响的刚度B可按下列规定计算:
1.采用荷载标准组合时

式中 Mk——按荷载的标准组合计算的弯矩,取计算区段内的最大弯矩值;
Mq——按荷载的准永久组合计算的弯矩,取计算区段内的最大弯矩值;
Bs——按荷载准永久组合计算的钢筋混凝土受弯构件或按标准组合计算的预应力混凝土受弯构件的短期刚度,按本规范第7.2.3条计算;
θ——考虑荷载长期作用对挠度增大的影响系数,按本规范第7.2.5条取用。
7.2.5 考虑荷载长期作用对挠度增大的影响系数θ可按下列规定取用:
2.预应力混凝土受弯构件,取θ=2.0。(https://www.xing528.com)
7.2.6 预应力混凝土受弯构件在使用阶段的预加力反拱值,可用结构力学方法按刚度EcI0进行计算,并应考虑预压应力长期作用的影响,计算中预应力筋的应力应扣除全部预应力损失。简化计算时,可将计算的反拱值乘以增大系数2.0。
【例7.4.7】 使用阶段挠度验算
条件:某预应力混凝土简支梁,跨度I0=9.75m,截面尺寸如图7.4.6所示,A0=12174.3mm2,I0=1.243×1010mm4,Ap=890.68mm2,Ap′=190.86mm2。
C50混凝土:Ec=3.45×104N/mm2
控制内力标准组合值为:Mk=499.08kN·m,
控制弯矩准永久组合值为:Mq=427.78 kN·m
完成全部预应力损失后预应力筋的总拉力为:Np0Ⅱ=935461N,偏心距ep0Ⅱ=265.8mm
要求:检验使用阶段的构件挠度。
答案:(1)求短期刚度Bs
因为构件裂缝抗裂等级为二级,根据《混规》第7.2.3条式(7.2.3-2),构件的短期刚度Bs为
Bs=0.85Es=0.85EcI0=0.85×3.45×104×1.243×1010
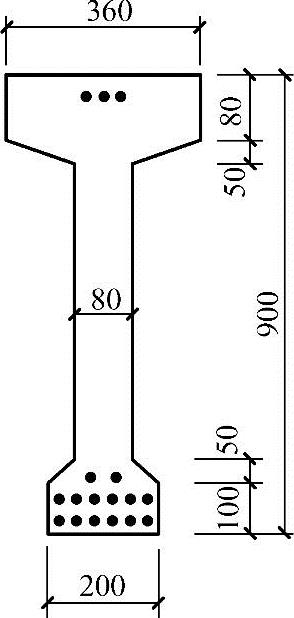
图 7.4.6
=3.645×1014N·mm2
(2)根据《混规》第7.2.2条式(7.2.2-2),长期刚度B为
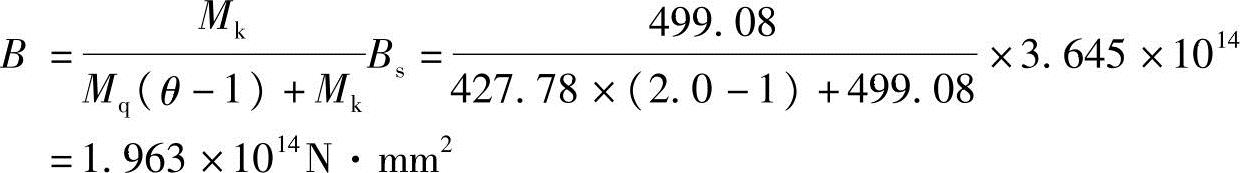
(3)标准荷载作用下构件的长期挠度为
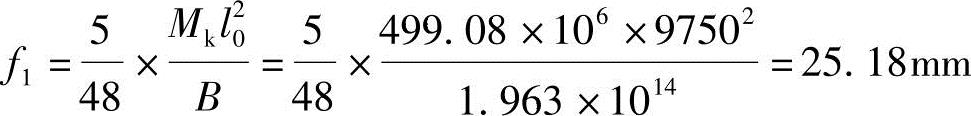
(4)计算预应力产生的反拱
认为沿梁全长均承受弯矩Np0Ⅱep0Ⅱ,按短期刚度求得反拱值后,再按《混规》第7.2.6条规定乘以挠度增大系数2,得到长期反拱值。
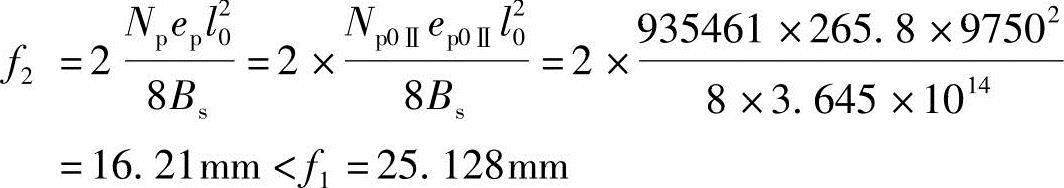
(5)构件的总挠度为
f=f1-f2=25.18-16.21=8.97mm
(6)根据《混规》第6.4.3条表3.4.3:
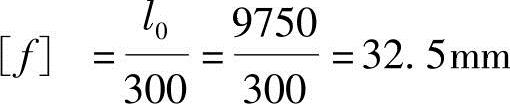
所以,f=8.97mm<[f]=32.5mm,使用阶段构件挠度满足要求。
【例7.4.8】 梁的长期刚度
条件:某单跨预应力钢筋混凝土屋面简支梁,混凝土强度等级为C40,计算跨度l0=17.7m,要求使用阶段不出现裂缝。该梁跨中截面按荷载效应的标准组合计算弯矩值Mk=800kN·m,按荷载效应准永久组合Mq=750kN·m,换算截面惯性距I0=3.4×1010mm4。
要求:求该梁按荷载效应标准组合并考虑荷载效应长期作用影响的刚度B(N·mm2)。
解答:查《混规》表4.1.5得Ec=3.25×104N/mm2
应用《混规》式(7.2.3-2)得短期刚度
Bs=0.85EcI0=0.85×3.25×104×3.4×1010N·mm2=9.393×1014N·mm2
根据《混规》第7.2.5条第2款,取影响系数θ=2.0
应用《混规》式7.2.2,得长期刚度:
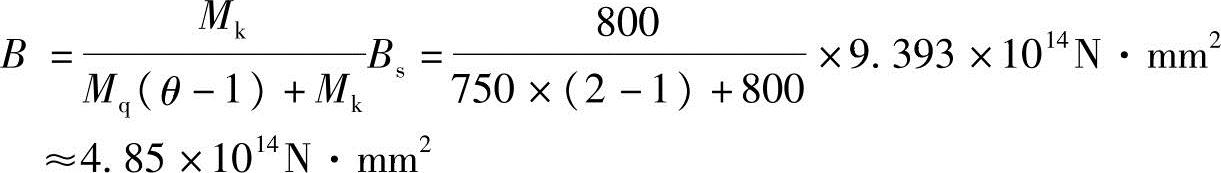
【例7.4.9】 挠度比
条件:仍讨论上题的单跨预应力钢筋混凝土屋面简支梁,该梁按荷载短期效应组合并考虑预应力长期作用产生的挠度f1=56.6mm,计算的预加力短期反拱值f2=15.2mm,该梁使用上对挠度有较高要求。
要求:求该梁挠度与《混凝土结构设计规范》中允许挠度[f]之比。
解答:根据《混规》第7.2.6条规定,考虑预压应力长期作用的影响,将计算求得的预加力短期反拱值f2乘以增大系数2.0,即f2=2×15.2mm=30.4mm。
根据《混规》第3.4.3条表3.4.3注3得梁的挠度:
f=f1-f2=(56.6-30.4)mm=26.2mm
查《混规》表3.4.3,l0>9m的对挠度有较高要求的构件挠度限值
[f]=l0/400=17700/400=44.25mm
该梁挠度与《混规》中允许挠度[f]之比为
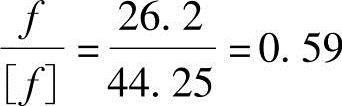
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




