挠度计算与最小刚度原则-混凝土结构

（一）考试要求

1.《考试大纲》的要求：一级掌握，二级了解

2.“试题”回顾

【试题5.3.7】 简支梁的跨中挠度（2001年）

某办公楼的钢筋混凝土简支梁，计算跨度l₀=6.90m，梁的截面尺寸为b×h=250mm×650mm。梁的混凝土强度等级为C25，钢筋为HRB335级。该梁承受均布恒载标准值（包括梁自重）g_k=16.20kN/m及均布活载标准值q_k=8.50kN/m。根据正截面受弯承载力计算结果，梁跨中下部配有纵向受拉钢筋320（A_s=941mm²），梁的混凝土保护层厚度c=25mm。

假定荷载短期效应组合的跨中最大弯矩M_s=M_gk+M_qk=96.41+50.59=147kN·m，B_s=5.5×10¹³ N·mm²，试确定该梁跨中挠度值f（mm）最接近于下列何项数值？

提示：该简支梁无受压钢筋；均布荷载作用下简支梁跨中挠度公式为。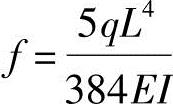

（A）f=23.75 （B）f=24.22 （C）f=30.13 （D）f=17.44

【试题5.3.8】 楼梯平台悬挑板的挠度（2006年）

已知图5.3.8a所示楼梯平台板在荷载效应标准组合作用下的短期刚度B_s=3.3×10¹²N·mm²，图5.3.8b表示楼梯平台板计算简图及折算均布荷载标准值（具体荷载值暂略）。当不考虑平台梁的扭转变形，只考虑板在竖向荷载作用下的变形时，试问平台板的最大挠度f（mm）与下列何项数值最为接近？

提示：①可变荷载的准永久值系数ψ_q=0.4，考虑荷载长期作用对挠度增大的影响系数θ=2.0。

②悬臂构件端部的挠度计算式为。

（A）1.3 （B）1.5 （C）2.0 （D）2.3

图 5.3.8

【试题5.3.9】 连续梁的挠度（2006年）

假定AB跨（即左端边跨）按荷载效应标准组合并考虑长期作用影响的跨中最大弯矩截面的刚度和B支座处的刚度，依次分别为B₁=8.0×10¹³N·mm²，B₂=6.0×10¹³N·mm²；作用在梁上的永久荷载标准值q_Gk=20kN/m，可变荷载标准值q_Qk=30kN/m。试问，AB跨中点处的挠度值f（mm），应与下列何项数值最为接近？

提示：在不同荷载分布作用下，AB跨中点挠度计算式如图5.3.9所示。

（A）20.5 （B）22.6

（C）30.4 （D）34.5

【试题5.3.10】 悬挑扳的挠度（2010年）

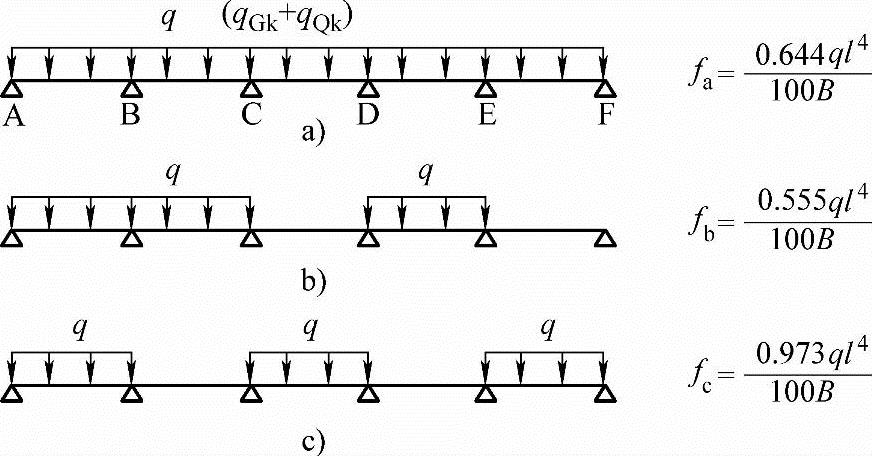
图 5.3.9

某钢筋混凝土不上人屋面挑檐剖面如图5.3.10所示，屋面板混凝土强度等级采用C30。屋面面层荷载相当于100mm厚水泥砂浆的重量，梁的转动忽略不计。板受力钢筋保护层厚度c=20mm。

假设挑檐根部按荷载效应标准组合计算的弯矩M_k=15.5kN·m，按荷载效应准永久组合计算的弯矩M_q=14.0kN·m，荷载效应的标准组合作用下受弯构件的短期刚度B_s=2.6×10¹²N·mm²，考虑荷载长期作用对挠度增大的影响系数θ=1.9。试问，该悬挑板的最大挠度（mm）与下列何项数值最为接近？

（A）8 （B）13

（C）16 （D）26

【试题5.3.11】 框架梁挠度（2012年一级）

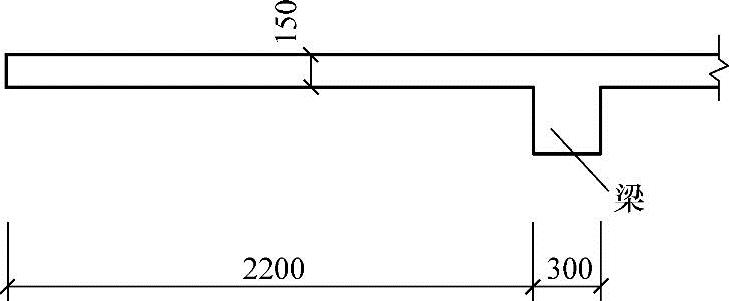
图 5.3.10

某钢筋混凝土框架结构多层办公楼局部平面布置如图5.3.11所示（均为办公室），梁、板、柱混凝土强度等级均为C30，梁、柱纵向钢筋为HRB400钢筋，楼板纵向钢筋及梁、柱箍筋为HRB335钢筋。

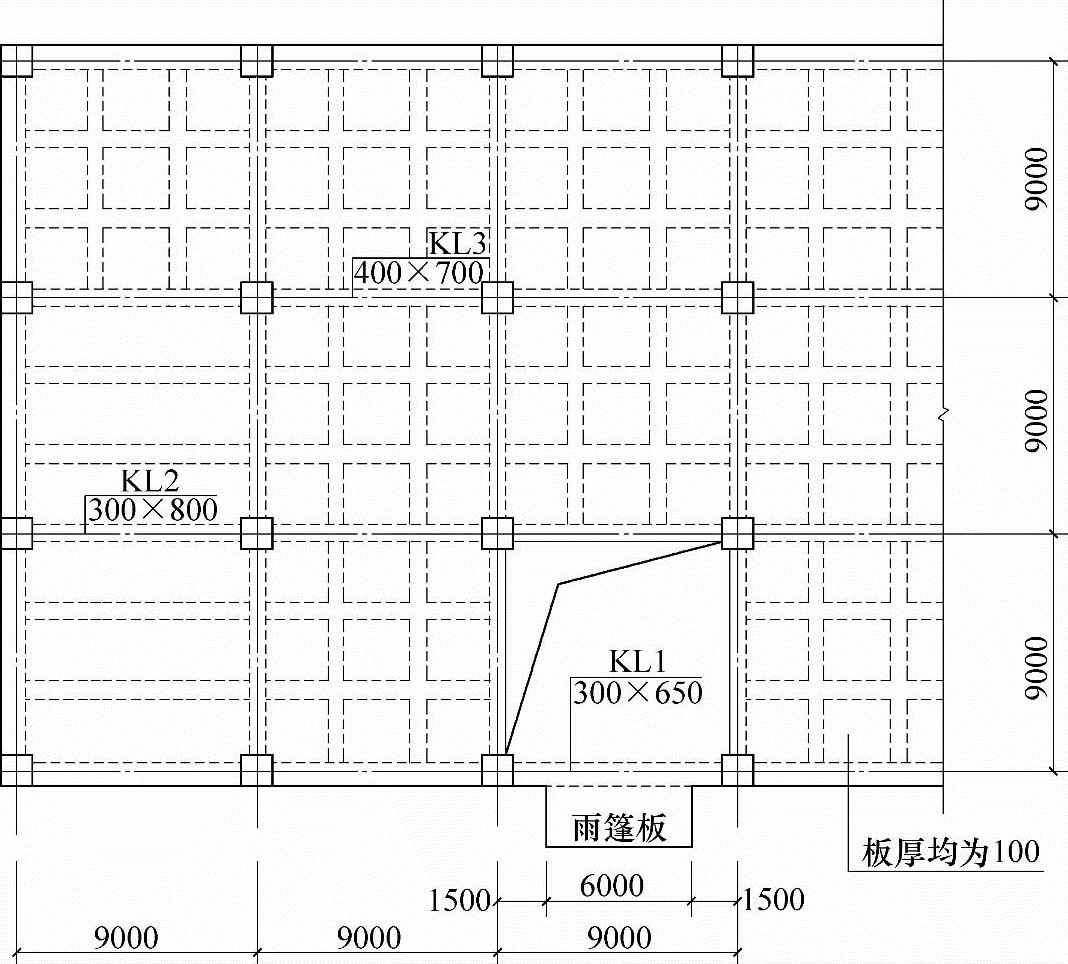
图 5.3.11

假设，框架梁KL2的左、右端截面考虑荷载长期作用影响的刚度B_A、B_B分别为9.0×10¹³N·mm²、6.0×10¹³N·mm²；跨中最大弯矩处纵向受拉钢筋应变不均匀系数ψ=0.8，梁底配置4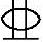25纵向钢筋。作用在梁上的均布静荷载、均布活荷载标准值分别为30kN/m、15kN/m。试问，按规范提供的简化方法，该梁考虑荷载长期作用影响的挠度f（mm）与下列何项数值最为接近？

提示：①按矩形截面梁计算，不考虑受压钢筋的作用，a_s=45mm。

②梁挠度近似按公式计算。

③不考虑梁起拱的影响。

（A）17 （B）21 （C）25 （D）30

（二）《混凝土结构设计规范》规定

《混凝土结构设计规范》规定：

7.2.1 钢筋混凝土和预应力混凝土受弯构件的挠度可按照结构力学方法计算，且不应超过本规范表3.4.3规定的限值。

在等截面构件中，可假定各同号弯矩区段内的刚度相等，并取用该区段内最大弯矩处的刚度。当计算跨度内的支座截面刚度不大于跨中截面刚度的2倍或不小于跨中截面刚度的1/2时，该跨也可按等刚度构件进行计算，其构件刚度可取跨中最大弯矩截面的刚度。

【例5.3.6】 梁的刚度

条件：图5.3.12所示为一两端承受弯矩的简支梁，计算跨度l₀=4.2m，矩形截面尺寸为b×h=200mm×400mm，C30级混凝土，纵向钢筋为HRB400。左端支座配置2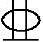12（A_sA=226mm²）；跨中配置312（A_s中=339mm²）；右端支座配置3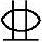14（A_sB=461mm²）。承受均布荷载，荷载准永久组合值：左端支座弯矩M_A=-16kN·m；右端支座弯矩M_B=-37kN·m，跨中弯矩M_中=48kN·m。

图 5.3.12

要求：计算该梁的刚度。

解答：从弯矩图中可以看出，简支梁跨间弯矩变号，将梁分为AC、CD、DB三段。按最小刚度原则，需分别求各段刚度。

现仅求AC段刚度，另两段刚度的计算过程不重复，仅列出计算结果。

有关参数：h₀=h-a_s=400-30-6=364mm

1.求AC段短期刚度B_s

（1）根据《混规》式（7.1.4-3），得裂缝截面处的钢筋应力σsq

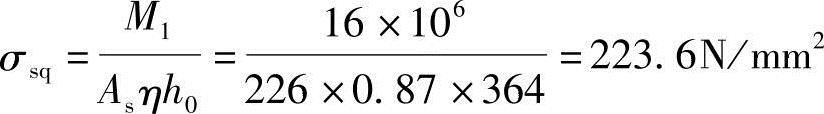
（2）根据《混规》式（7.1.2-4），得按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte

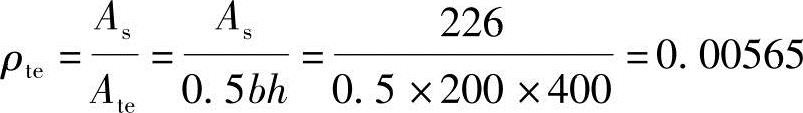
（3）根据《混规》式（7.1.2-2），得纵向受拉钢筋应变不均匀系数ψ：

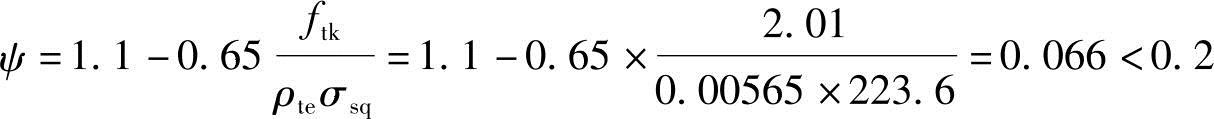，取ψ=0.2

（4）根据《混规》式（7.1.4-7）得矩形截面γ_f′=0。

（5）根据《混规》第7.2.3条：

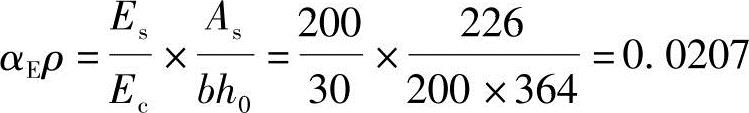
（6）根据《混规》式（7.2.3-1）计算短期刚度

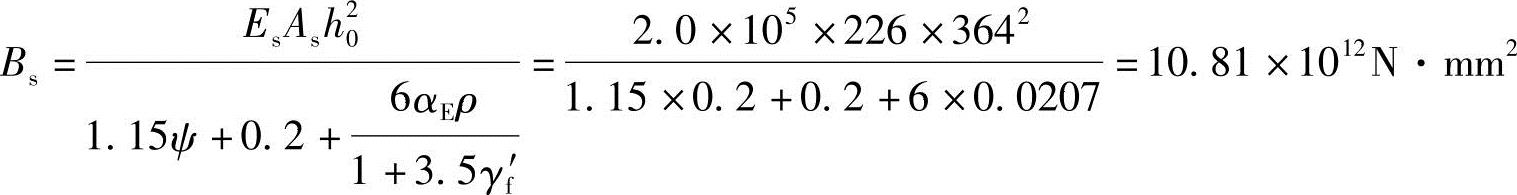
2.求AC段长期作用影响刚度B

（1）根据《混规》第7.2.5条计算增大系数θ。设ρ′=ρ，故θ=1.6。

（2）根据《混规》式（7.2.2-2），可得该梁按荷载准永久组合并考虑荷载长期作用影响的刚度，即：

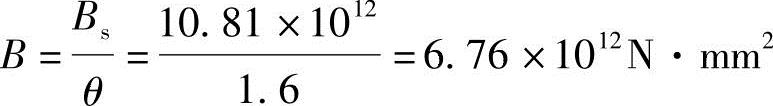
同样可求出CD段和DB段的刚度，现将计算结果列于表5.3.1和图5.3.13，计算过程不再重复。

表5.3.1 各段刚度

图5.3.13 各段刚度示意

现根据《混规》的下列规定进行讨论。

7.2.1 当计算跨度内的支座截面刚度不大于跨中截面刚度的2倍或不小于跨中截面刚度的1/2时，该跨也可按等刚度构件进行计算，其构件刚度可取跨中最大弯矩截面的刚度。讨论内容列于表5.3.2。

表5.3.2 刚度的比较 （单位：10¹²N·mm²）

讨论结果表明本题符合《混规》第7.2.1条的规定，故按等刚度梁进行计算，梁的刚度可取跨中最大弯矩截面的刚度，即B=5.05×10¹²N·mm²。

【例5.3.7】 连续梁的挠度值

条件：某钢筋混凝土五跨连续梁。其计算简图如图5.3.14所示。AB跨（即左端边跨）按荷载效应准永久组合并考虑长期作用影响的跨中最大弯矩截面的刚度和B支座处的刚度，依次分别为B₁=8.4×10¹³N·mm²，B₂=6.5×10¹³N·mm²，作用在梁上的永久荷载标准值q_Gk=15kN/m，可变荷载标准值q_Qk=30kN/m。

要求：求AB跨中点处的挠度值f（mm）。

提示：在不同荷载分布作用下，AB跨中点挠度计算式如图5.3.15中所示，ψ_q=0.4。

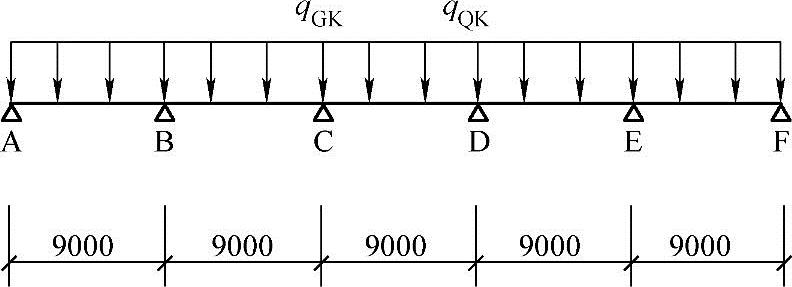
图 5.3.14

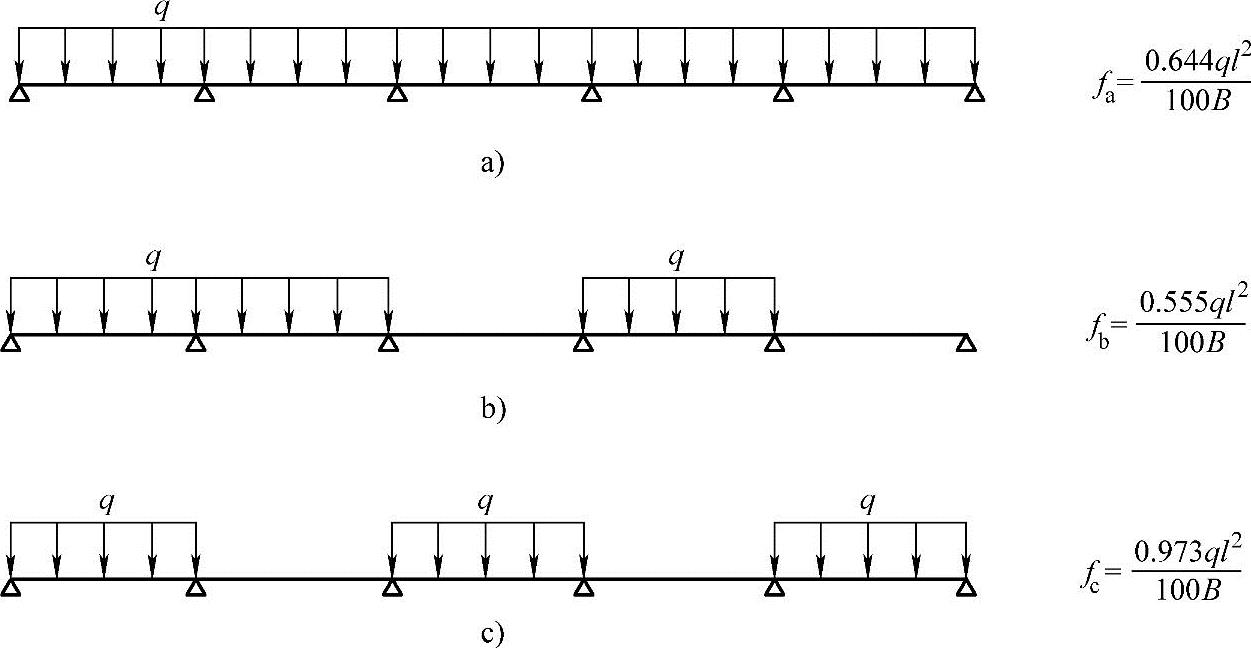
图 5.3.15

解答：

跨中B₁=8.4×10¹³N·mm²

支座B₂=6.5×10¹³N·mm²>跨中B₁/2=4.2×10¹³N·mm²

B₂=6.5×10¹³N·mm²<2B₁=16.8×10¹³N·mm2

根据《混规》第7.2.1条：B₂<2B₁且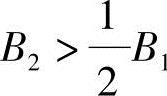，按跨中等刚度计算。

故AB跨按等刚度计算，取B=B₁=8.4×10¹³ N·mm²

又恒载q_Gk=15kN/m，活载q_Qk=30kN/m。

当恒载满跨布置，活载隔跨布置时，挠度最大。

所以

（三）计算步骤与算例

计算步骤

已知：b，h，b_f′，h_f′，b_f，h_f，l₀，f_tk；E_c，A_s，A_s′，E_s，M_q；求挠度f。

计算有关参数：f_lim，h₀，ρ=A_s/bh₀，ρ′=A_s′/bh₀，α_E=E_s/E_c。

（1）根据《混凝土结构设计规范》式（7.1.4-3）得裂缝截面处的钢筋应力σ_sq，。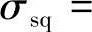

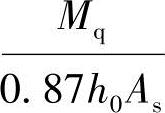（2）根据《混凝土结构设计规范》式（7.1.2-4），按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρ_te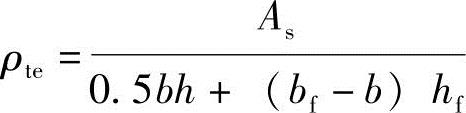：，取在裂缝宽度计算中ρ_te≥0.01，而挠度计算时不执行此项。

（3）根据《混凝土结构设计规范》式（7.1.2-2），得纵向受拉钢筋应变不均匀系数，取0.2≤ψ≤1.0

（4）根据《混凝土结构设计规范》式（7.1.4-7）

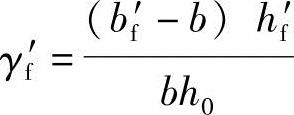
h_f′>0.2h₀，取h_f′=0.2h₀

（5）根据《混凝土结构设计规范》第7.2.3条和第7.2.5条的符号说明

ρ=A_s/（bh₀），ρ′=A_s′/（bh₀），α_E=E_s/E_c

（6）根据《混凝土结构设计规范》式（7.2.3-1）计算短期刚度

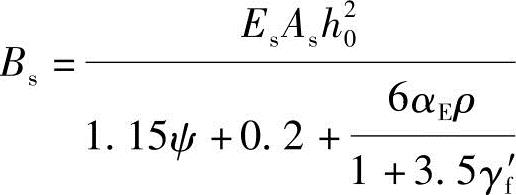
（7）根据《混凝土结构设计规范》第7.2.5条计算长期作用对挠度增大的影响系数

倒T形截面，θ值增加20%。

（8）根据《混凝土结构设计规范》式（7.2.2-2）得该梁按荷载准永久组合并考虑荷载长期作用影响的刚度

（9）可按简支梁求得该构件的挠度

【例5.3.8】 矩形截面简支梁的挠度

条件：某办公楼钢筋混凝土简支梁的计算跨度l₀=6.9m，截面尺寸为b×h=250mm×650mm，环境类别为二a级。梁承受均布恒载标准值（包括梁自重）g_k=16.20kN/m，均布活荷载标准值q_k=8.50kN/m。准永久值系数ψ_q=0.4。混凝土强度等级为C30（f_tk=2.01N/mm²，E_c=3.0×10⁴N/mm²），采用HRB400级钢筋（E_s=2.0×10⁵N/mm²）。由正截面受弯承载力计算配置3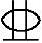20（A_s=941mm²），梁的挠度限值f_lim=l₀/200。

要求：验算梁的挠度是否满足要求。

解答：已知b=250mm，h=650mm，a_s=35mm，h₀=h-a_s=650-35=615mm，A_s=941mm²。

C30混凝土：f_tk=2.01N/mm²；E_c=3.00×10⁴N/mm²，E_s=2.00×10⁵N/mm²。

有关参数计算如下：f_lim=l₀/200=34.5mm。

准永久组合的弯矩值：

（1）根据《混规》式（7.1.4-3）得裂缝截面处的钢筋应力σsq

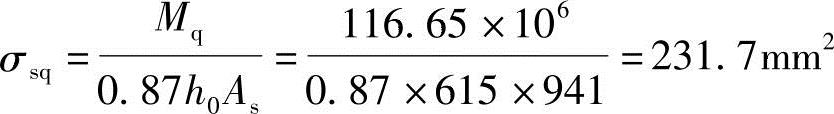
（2）根据《混规》式（7.1.2-4），按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte

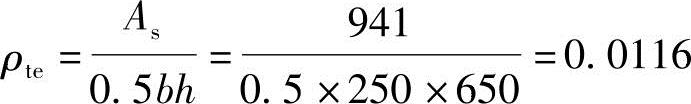
（3）根据《混规》式（7.1.2-2）得纵向受拉钢筋应变不均匀系数ψ

(www.xing528.com)

（4）根据《混规》式（7.1.4-7），取矩形截面γ_f′=0。

（5）根据《混规》第7.2.3条：

（6）根据《混规》式（7.2.3-1）计算短期刚度：

（7）根据《混规》第7.2.5条计算增大系数θ。由于ρ′=0，故θ=2.0。

（8）根据《混规》式（7.2.2-2）可得该梁按荷载准永久组合并考虑荷载长期作用影响的刚度，即：

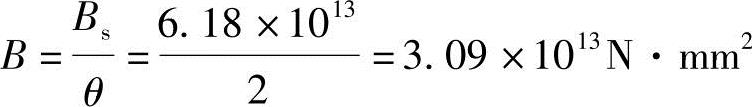
（9）计算梁的挠度：

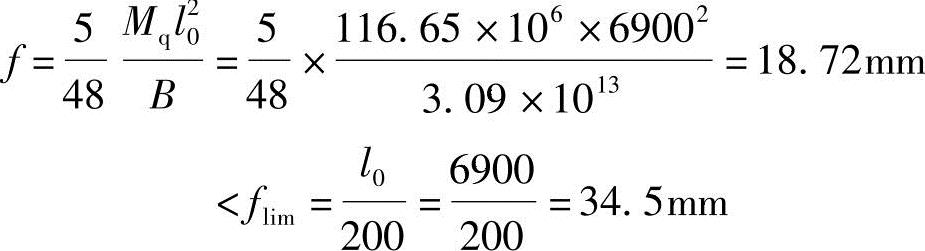
符合要求。

【例5.3.9】 矩形截面简支梁的挠度

条件：某矩形截面钢筋混凝土简支梁如图5.3.16所示，计算跨度l₀=6m，截面尺寸为200mm×500mm，环境类别为一类，混凝土设计强度等级为C30，梁底配216+220、HRB500级纵向受拉钢筋，梁顶配214（HRB500级）纵向受压钢筋，钢筋保护层厚度c=20mm，承受荷载效应的准永久组合弯矩M_q=100kN·m，挠度限值[f]=l₀/200，a_s=35mm。

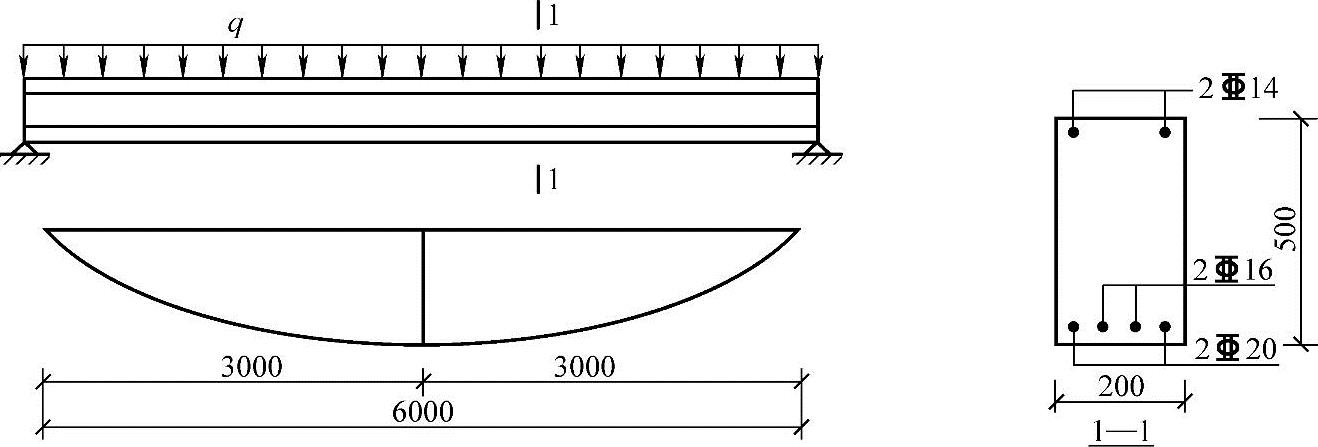
图 5.3.16

要求：验算梁的挠度是否满足要求。

解答：已知：l₀=6m，b=200mm，h=500mm，h₀=465mm，A_s=1030mm²，A_s′=308mm²，C30混凝土，f_tk=2.01N/mm²，E_c=3.00×10⁴N/mm²，E_s=2.00×10⁵N/mm²。

（1）根据《混规》式（7.1.4-3）得裂缝截面处的钢筋应力σ_sq：

（2）根据《混规》式（7.1.2-4），按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρ_te：

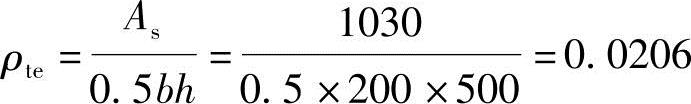
（3）根据《混规》式（7.1.2-2）得纵向受拉钢筋应变不均匀系数ψ

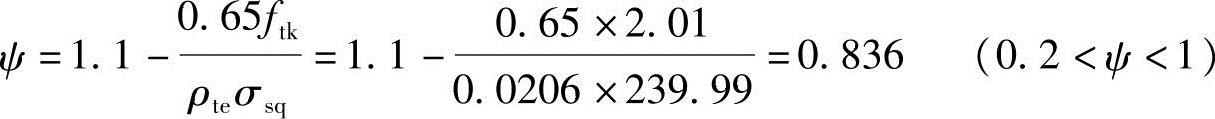
（4）根据《混规》式（7.1.4-7），取矩形截面γ_f′=0。

（5）根据《混规》第7.2.3条：

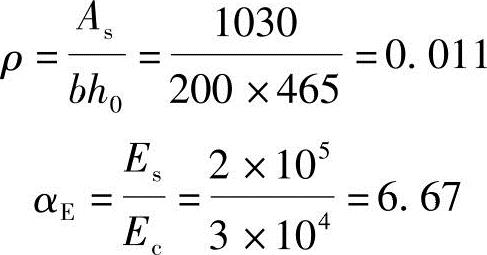
根据《混规》第7.2.5条：

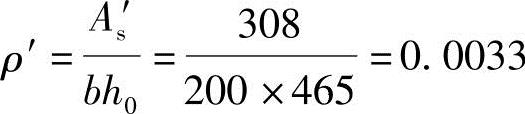
（6）根据《混规》式（7.2.3-1）计算短期刚度

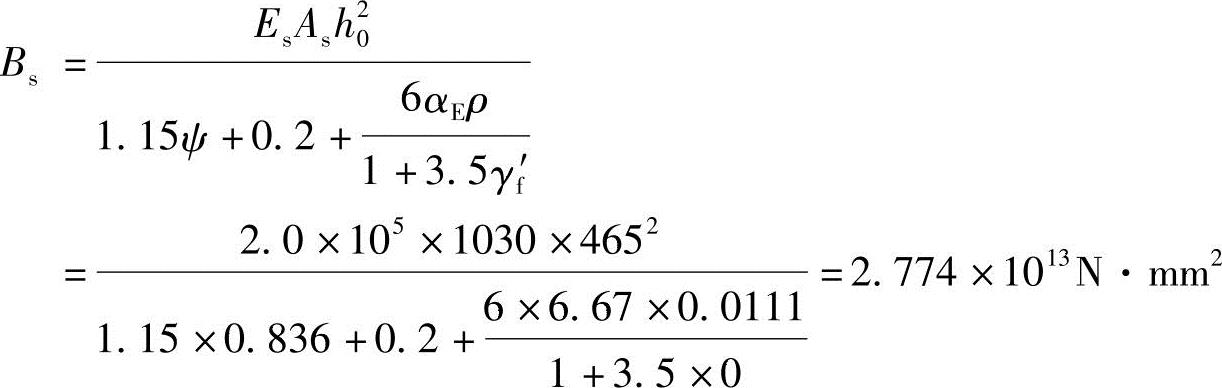
（7）根据《混规》第7.2.5条计算增大系数θ

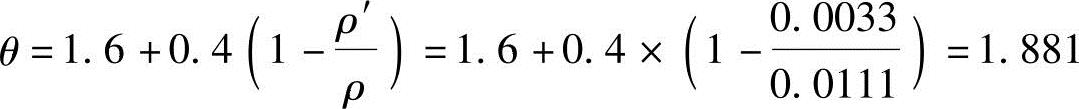
（8）根据《混规》式（7.2.2-2）可得该梁按荷载准永久组合并考虑荷载长期作用影响的刚度，即

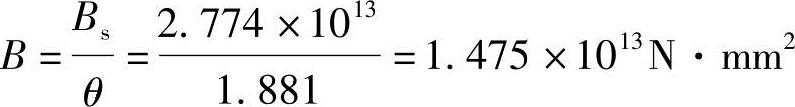
（9）可按简支梁求得该构件的挠度

满足要求。

【例5.3.10】 T形截面简支梁的挠度

条件：已知T形截面简支梁，处于室内正常环境，计算跨度l₀=6m，截面尺寸b=200mm，h=550mm，b_f′=550mm，h_f′=80mm；混凝土强度等级为C30，纵向受拉钢筋320（采用HRB400级）；箍筋直径为8mm，按荷载准永久组合计算的跨中最大弯矩值M_q=69.75kN·m。

要求：验算该梁挠度是否满足要求。

解答：已知：b=200mm，h=550mm，b_f′=550mm，h_f′=80mm，l₀=6m，C30混凝土。f_tk=2.01N/mm²；E_c=3.00×10⁴N/mm²，A_s=942mm²（320），E_s=2.00×10⁵N/mm²，M_q=69.75kN·m。

有关参数计算如下：

根据《混规》表3.4.3可得该板的挠度限值为f_lim=l₀/200=6000/200=30mm。

根据《混规》第8.2.1条可知，室内正常环境对应的环境类别为一类，其最外层钢筋的混凝土保护层厚度为c=20mm，箍筋直径ϕ=8mm，则：

a_s=c+ϕ+d/2=20+8+20/2=38mm

截面有效高度：h₀=h-a_s=550-38=512mm

（1）根据《混规》式（7.1.4-3）得裂缝截面处的钢筋应力σ_sq：

（2）根据《混规》式（7.1.2-4），按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte

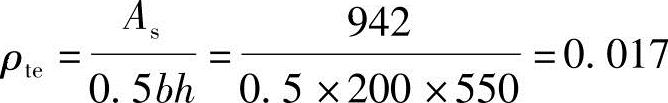
故取ρ_te=0.017。

（3）根据《混规》式（7.1.2-2）可得纵向受拉钢筋应变不均匀系数，即

故取ψ=0.638。

（4）根据《混规》式（7.1.4-7）：

（5）根据《混规》第7.2.3条：

（6）根据《混规》式（7.2.3-1）计算短期刚度

（7）根据《混规》第7.2.5条计算增大系数θ：

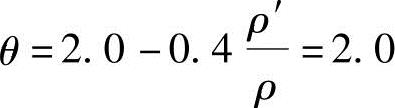
（8）根据《混规》式（7.2.2-2），可得该梁按荷载准永久组合并考虑荷载长期作用影响的刚度，即：

（9）可按简支梁求得该构件的挠度：

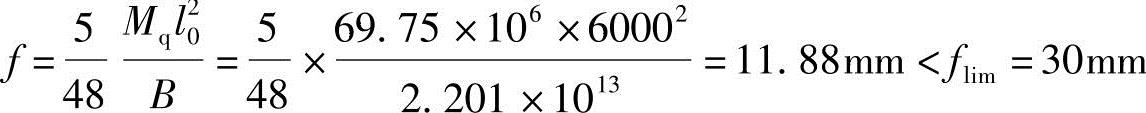
满足要求。

（四）模拟考题

【5.3.1】～【5.3.5】 混凝土T形截面简支梁属于一类室内正常环境的一般构件，计算跨度6m，截面尺寸b=250mm，h=650mm，b_f′=800mm，h_f′=120mm，a_s=70mm；采用C30级混凝土，纵筋采用HRB400级钢筋。

【5.3.1】 若配置8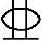25受拉钢筋，则ρ_te最接近下列何项数值？

（A）0.051 （B）0.048 （C）0.024 （D）0.036

答案：（B）

A_s=8×490.9=3927.2mm²

根据《混规》第7.1.2条的规定：

A_te=0.5bh=0.5×250×650=81250mm²

由《混规》式（7.1.2-4）得：

【5.3.2】 若梁上作用均布静载g_k=35kN/m（包括梁自重），均布活载q_k=28kN/m（ψ_q=0.5），跨中作用集中静载G_k=95kN，集中活载Q_k=128kN（ψ_q=0.4）。则M_q（kN·m）最接近下列何项数？

（A）427.2 （B）618.0 （C）439.8 （D）459.0

答案：（C）

根据《混规》式（3.2.10）得：

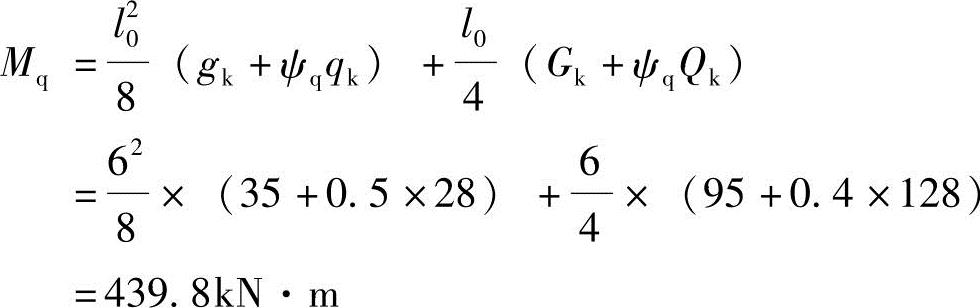
【5.3.3】 若M_q=571kN·m，ρ_te=0.06，则ψ最接近下列何项数值？

（A）0.978 （B）1.0 （C）1.103 （D）1.024

答案：（B）

f_tk=2.01N/mm²，a_s=70mm，h₀=580mm

由《混规》式（7.1.4-3）得：

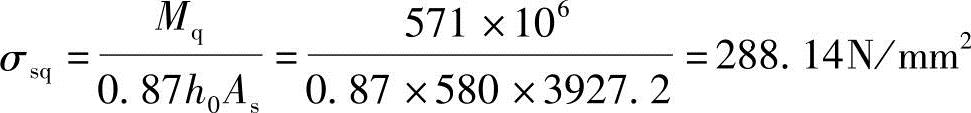
由《混规》式（7.1.2-2）：

【5.3.4】 若ψ=0.978，则B_s（×10¹⁴N·mm²）最接近下列何项数值？

（A）1.087 （B）1.099 （C）1.496 （D）1.517

答案：（D）

E_c=3×10⁴N/mm²，f_y=360N/mm²，E_s=2×10⁵N/mm2

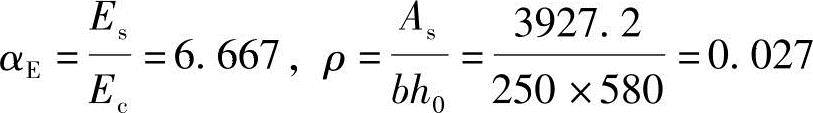
由《混规》式（7.1.4-7）得：

由《混规》式（7.2.3-1）得：

【5.3.5】 梁上作用均布荷载准永久值g_k+ψ_qq_k=105.0kN/m，B_s=2.12×10¹⁴N·mm²，则梁的最大挠度f（mm）最接近下列何项数值？

（A）18.61 （B）16.18 （C）16.72 （D）12.27

答案：（C）

根据《混规》第7.2.5条，取θ=2.0。

由《混规》式（7.2.2-2）得：

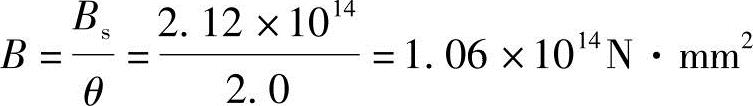
挠度计算：

【5.3.6】 为提高钢筋混凝土受弯构件的刚度，下列措施中哪几项是正确的？

（A）加大截面高度 （B）加大纵向受拉钢筋截面面积

（C）加大纵向受压钢筋截面面积 （D）提高混凝土强度等级

（E）保持受拉纵筋配筋率不变，采用较小直径钢筋

答案：（A）、（B）、（C）、（D）

由《混规》式（7.2.3-1）、式（7.1.2-2）、式（7.1.2-4）、式（7.1.4-3）及第7.2.5条

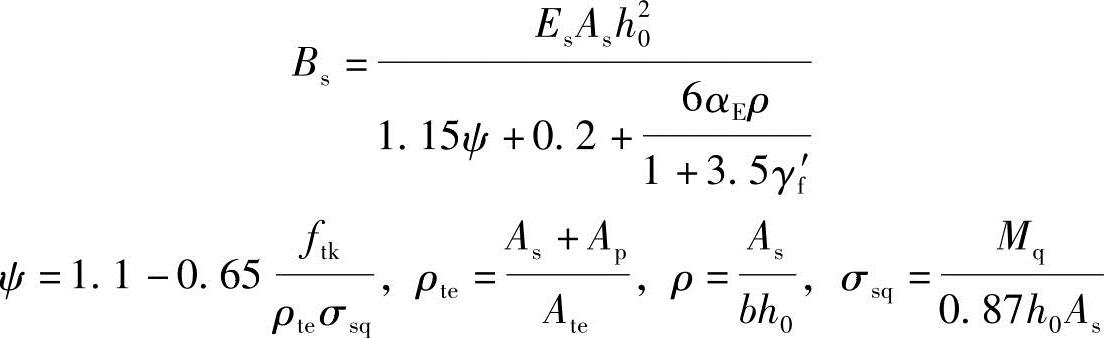
（A）B_s与h²₀成正比的增大，加大截面高度对提高构件刚度最有效。

（B）B_s与A_s成正比的增大，同时σ_sq随A_s增大而减小，使ψ减小，也使B_s增大。

（C）A_s′增大，使θ减小，使长期刚度B增大；但不及A_s显著。

（D）提高混凝土强度等级，使f_tk和E_c增大，ψ随f_tk增大而降低；α_E随E_c增大而降低；均使B_s提高。

（E）保持ρ不变，采用较小直径钢筋，可使裂缝宽度减小，对提高刚度无效。

【5.3.7】 某钢筋混凝土简支大梁，矩形截面，混凝土强度等级为C30。根据《混凝土结构设计规范》公式求出梁的挠度和裂缝稍大，需调整设计，但荷载和截面不能改变。下列减少f和w_max的几种办法中，哪几项措施是合适的？

（A）提高混凝土的强度等级

（B）取消受压钢筋（A_s′=0），同时增加剪力箍筋A_sv和缩小剪力箍筋间距s

（C）增加受拉钢筋（A_s）的截面面积

（D）增加受压钢筋（A_s′）的截面面积和减少受拉主筋的钢筋直径d

答案：（A）、（C）、（D）

由《混规》式（7.2.3-1）、式（7.1.2-2）、式（7.1.2-4）、式（7.1.4-3），取消受压钢筋（A_s′=0），同时增加剪力箍筋A_sv和缩小剪力箍筋间距s，对提高刚度无效。故（B）是错误的。