(一)《混凝土结构设计规范》规定
1.受扭塑性抵抗矩Wt
对T形和I形截面受扭构件,将截面划分为数个矩形截面,其原则是:先按截面总高度确定腹板截面,然后再划分受压和受拉翼缘(图4.2.10),对腹板、受压翼缘及受拉翼缘部分的矩形截面受扭塑性抵抗矩可按《混凝土结构设计规范》第6.4.3条的规定计算。
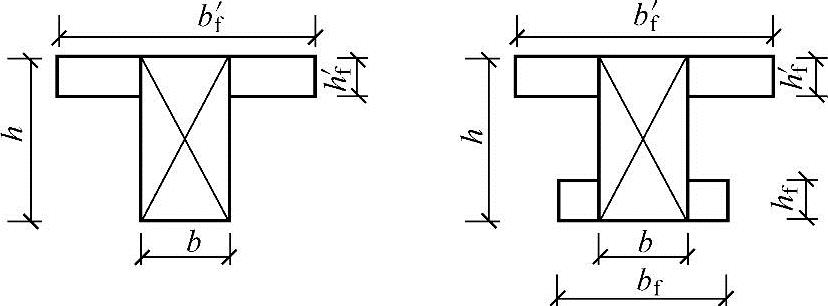
图 4.2.10
《混凝土结构设计规范》规定:
6.4.3 受扭构件的截面受扭塑性抵抗矩可按下列规定计算:
2.T形和I形截面
Wt=Wtw+Wt′f+Wtf (6.4.3-2)
腹板、受压翼缘及受拉翼缘部分的矩形截面受扭塑性抵抗矩Wtw、Wt′f和Wtf,可按下列规定计算:
1)腹板

2)受压翼缘

3)受拉翼缘

式中 b、h——截面的腹板宽度、截面高度;
bf′、bf——截面受压区、受拉区的翼缘宽度;
hf′、hf——截面受压区、受拉区的翼缘高度。
计算时取用的翼缘宽度尚应符合bf′不大于b+6hf′及bf不大于b+6hf的规定。
2.扭矩的分配
对T形和I形截面受扭构件,每个矩形截面的扭矩设计值可按《混凝土结构设计规范》第
6.4.5条的规定计算。
《混凝土结构设计规范》规定:
6.4.5 T形和I形截面纯扭构件,可将其截面划分为几个矩形截面,分别按本规范第
6.4.4条进行受扭承载力计算。每个矩形截面的扭矩设计值可按下列规定计算:
1)腹板

2)受压翼缘

3)受拉翼缘

式中 Tw——腹板所承受的扭矩设计值;
Tf′、Tf——受压翼缘、受拉翼缘所承受的扭矩设计值。
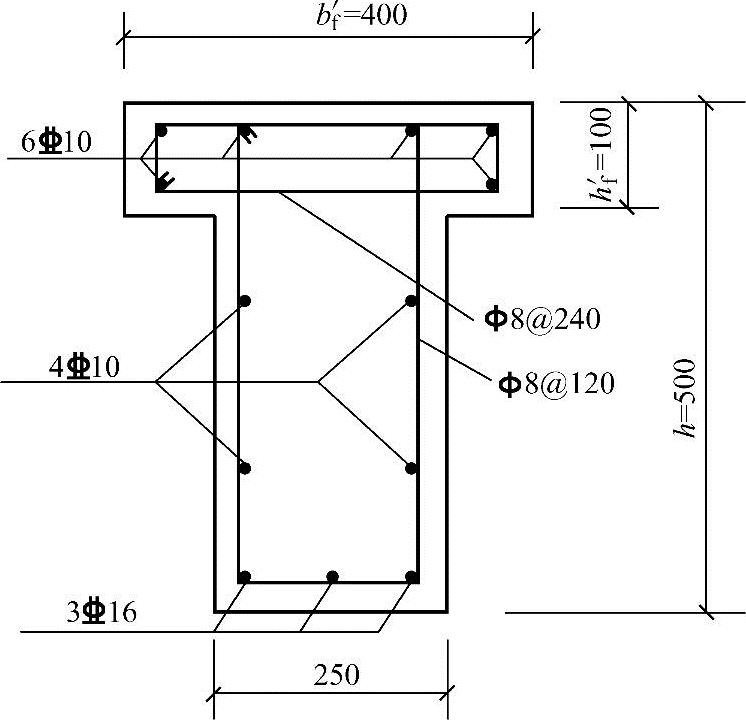
图 4.2.11
(二)算例
【例4.2.1】 T形截面纯扭构件的扭矩分配
条件:已知混凝土T形截面受扭构件(图4.2.11)bf′=400mm,hf′=100mm,b=250mm,h=500mm,承受扭矩设计值T=12.7kN·m。
要求:(1)求受扭塑性抵抗矩;
(2)求腹板、翼缘分担的扭矩。
解答:(1)受扭塑性抵抗矩
根据《混规》式(6.4.3-3)、式(6.4.3-4):
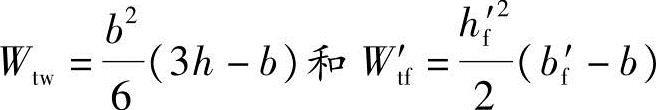
腹板的受扭塑性抵抗矩:
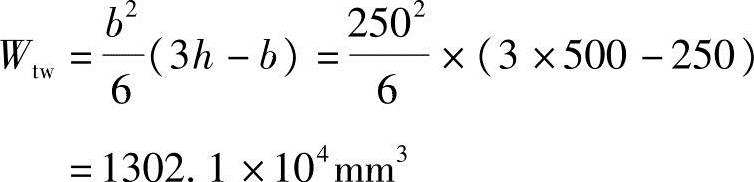
翼缘的受扭塑性抵抗矩:
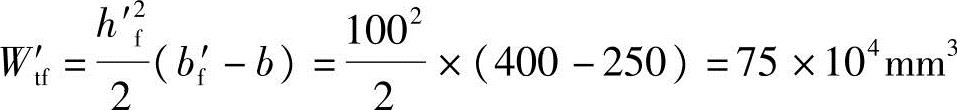
bf′=400mm<b+6hf′=250+6×100=850mm
根据《混规》式(6.4.3-2),Wt=Wtw+Wt′f+Wtf,截面的受扭塑性抵抗矩
Wt=Wtw+Wtf′=(1302.1+75)×104=1377.1×104mm3
(2)扭矩的分配
根据《混规》式(6.4.5-1)、式(6.4.5-2):(https://www.xing528.com)
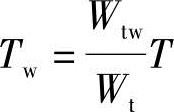 与
与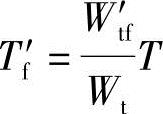
腹板的扭矩 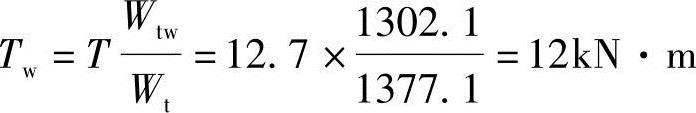
翼缘的扭矩 Tf′=12.7-12.0=0.7kN·m
(三)模拟考题
【4.2.1】 钢筋混凝土T形截面构件,b=250mm,h=500mm,bf′=400mm,hf′=150mm。若构件承受的扭矩设计值T=15kN·m,则截面上翼缘分配的扭矩Tf′(kN·m)与下列何项数值最为接近?
(A)1.72 (B)1.43 (C)1.60 (D)1.25
答案:(A)
Ⅰ.详细解答
(1)求受扭塑性抵抗矩:根据《混规》第6.4.3条,T形截面受扭塑性抵抗矩Wt=Wtw+Wt′f+Wtf
由《混规》式(6.4.3-3)知腹板的受扭塑性抵抗矩:
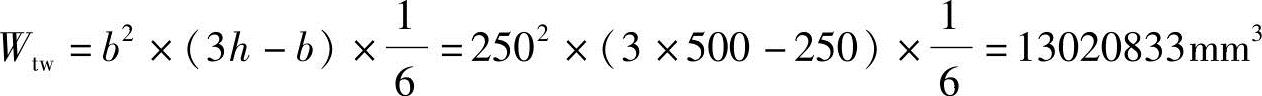
由《混规》式(6.4.3-4)知受压翼缘的受扭塑性抵抗矩:
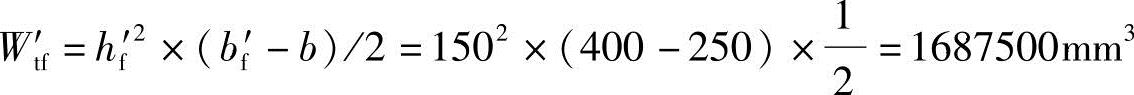
由《混规》式(6.4.3-2)知截面的总受扭塑性抵抗矩:
Wt=Wtw+Wtf=13020833+1687500=14708333mm3
(2)扭矩的分配根据《混规》第6.4.5条计算,腹板和翼缘扭矩的分配按《混规》式(6.4.5-1)和式(6.4.5-2):
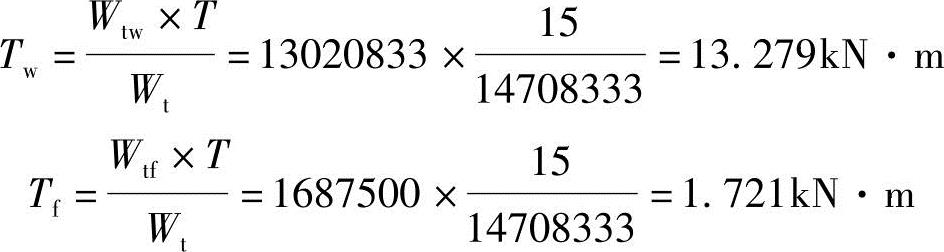
Ⅱ.简要解答
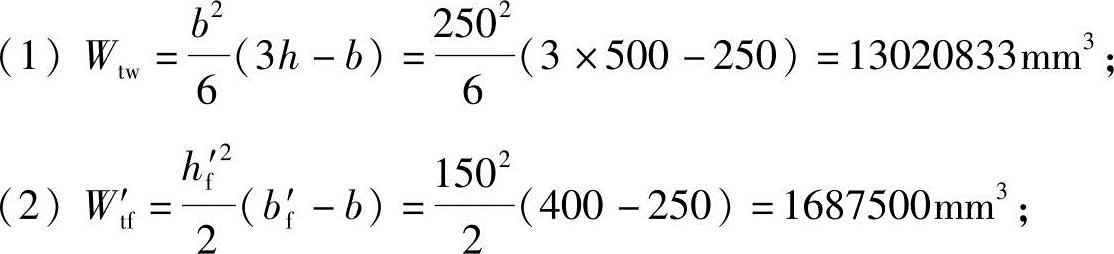
(3)Wt=Wtw+Wt′f=13020833+1687500=14708333mm3;
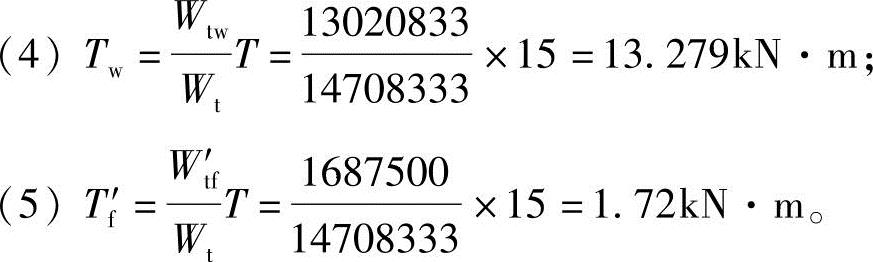
【4.2.2】 一非对称钢筋混凝土I形梁截面尺寸如图4.2.12所示,混凝土为C20,宽度b=300mm,高度h=500mm,受拉区翼缘宽度bf=800mm,受拉区翼缘高度h=80mm,受压区翼缘宽度bf′=600mm,受压区翼缘高度hf′=80mm。设截面的扭矩设计值T=20kN·m,则截面腹板所承受的扭矩值(kN·m)与何项数值最为接近?
(A)18.901 (B)17.564
(C)16.684 (D)19.013
答案:(B)
Ⅰ.详细解答
(1)求受扭塑性抵抗矩
由《混规》第6.4.3条知:
I形截面受扭塑性抵抗矩Wt=Wtw+W′tf+Wtf。
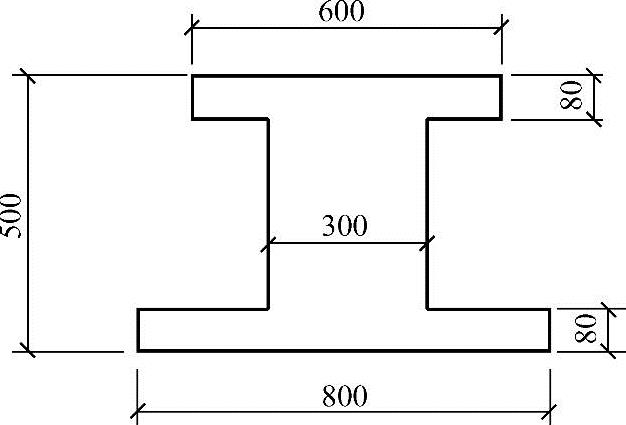
图 4.2.12
由《混规》式(6.4.3-3)知腹板的受扭塑性抵抗矩
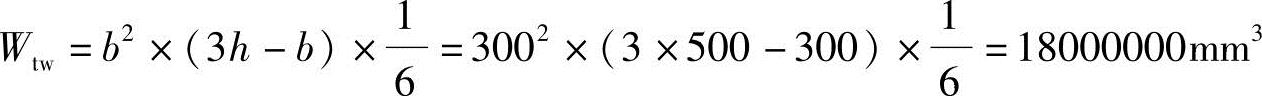
由《混规》式(6.4.3-4)知受压翼缘的受扭塑性抵抗矩
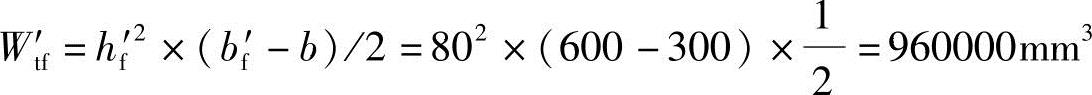
由《混规》式(6.4.3-5)知受拉翼缘的受扭塑性抵抗矩
Wtf=h2f×(bf-b)/2
bf=800mm>b+6×hf=300+6×80=780mm,取bf=780mm
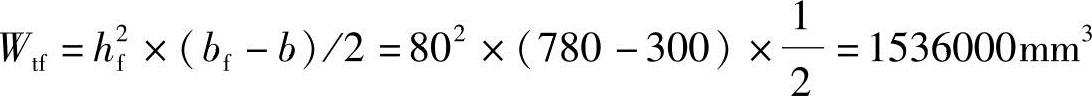
由《混规》式(6.4.3-2)知截面的总受扭塑性抵抗矩
Wt=Wtw+Wtf+Wt′f=18000000+1536000+960000=2049600mm3
(2)扭矩的分配:根据《混规》6.4.5条,腹板和翼缘扭矩的分配分别按《混规》式(6.4.5-1)、式(6.4.5-2)、式(6.4.5-3)计算:
腹板:
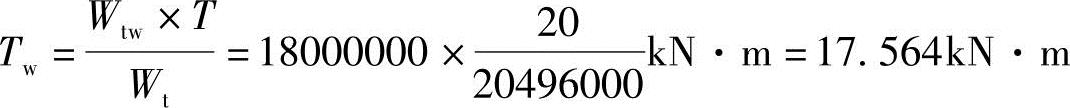
受拉翼缘:
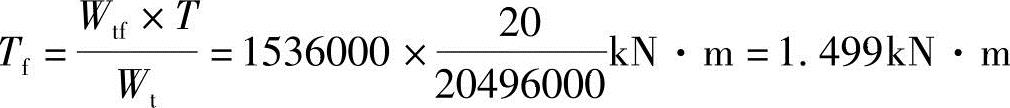
受压翼缘:
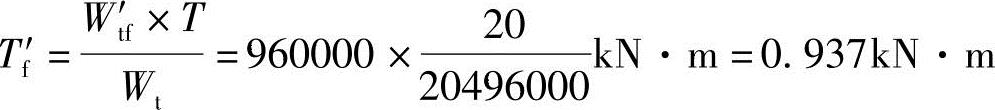
Ⅱ.简要解答
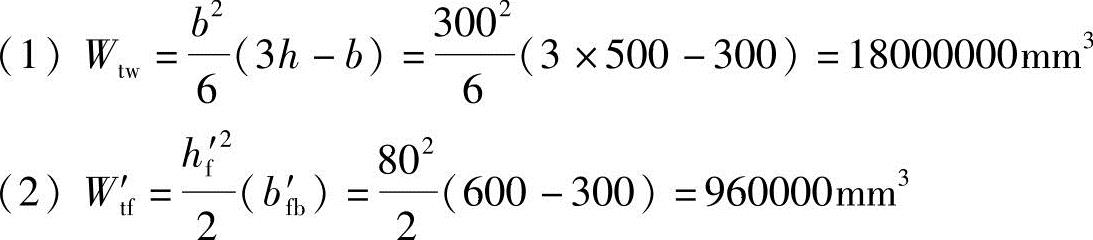
(3)bf=800=b+6hf=300+6×80=780mm,取bf=780mm

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




