(一)偏心距
1.考试要求
(1)《考试大纲》的要求:掌握
(2)“试题”回顾
【试题3.3.14】 大小偏心受压判断(1999年)
在对钢筋混凝土偏心受压构件作大小偏心受压判断时,下列何项论述正确?
(A)轴向力作用在截面核心区以内时为小偏心受压,反之为大偏心受压
(B)轴向力作用在截面范围内时为小偏心受压,反之为大偏心受压
(C)相对受压区高度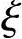 ≤
≤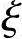 b时为大偏心受压,反之为小偏心受压(
b时为大偏心受压,反之为小偏心受压(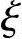 b为相对界限受压区高度)
b为相对界限受压区高度)
(D)ηi≤0.3h0时为小偏心受压,反之为大偏心受压(η为偏心受压构件考虑挠曲影响的轴向力偏心距增大系数,ei为初始偏心距)。
【试题3.3.15】 楼梯柱的偏心距es′(2006年)
楼梯梁TL-1及楼梯柱TZ-1的计算简图如图3.3.20所示。假定楼梯柱TZ-1承受的轴力设计值N=150kN,弯矩设计值M=35kN·m。试问,当进行正截面受压承载力计算时,轴向压力作用点至纵向受压钢筋合力点的距离e′(m),应与以下何项数值最为接近?
提示:对称配筋,as=as′=40mm,η=1.2。
(A)116 (B)194
(C)306 (D)416
2.《混凝土结构设计规范》规定和算例
《混凝土结构设计规范》规定:
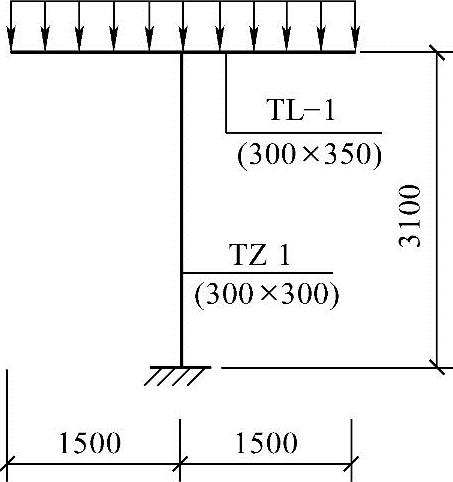
图 3.3.20
6.2.17

ei=e0+ea(6.2.17-4)
式中 e——轴向压力作用点至纵向受拉普通钢筋和受拉预应力筋的合力点的距离:
e0——轴向压力对截面重心的偏心距,取为M/N,当需要考虑二阶效应时,M为按本
规范第5.3.4条、第6.2.4条规定确定的弯矩设计值;
ea——附加偏心距,按本规范第6.2.5条确定;
ei——初始偏心距;
a——纵向受拉普通钢筋和受拉预应力筋的合力点至截面近边缘的距离。
6.2.5 偏心受压构件的正截面承载力计算时,应计入轴向压力在偏心方向存在的附加偏心距ea,其值应取20mm和偏心方向截面最大尺寸的1/30两者中的较大值。
【例3.3.11】 附加偏心距
偏心受压柱b=300mm,h=500mm,则附加偏心距ea(mm)最接近下列何项数值?
(A)30 (B)16.7 (C)20 (D)25
答案:(C)
根据《混规》第6.2.5条的规定:
附加偏心距ea=max(20,h/30)=max(20,500/30=16.7)=20mm
【例3.3.12】 轴向压力作用点至纵向受压钢筋合力点的距离e′
图3.3.21所示钢筋混凝土偏压柱、对称配筋,a=a′s=40mm。承受的轴力设计值N=150kN,弯矩设计值M=35kN·m,试问,当进行正截面受压承载力计算时,轴向压力作用点至纵向受压钢筋合力点的距离e′(mm),应与以下何项数值最为接近?
(A)116 (B)146 (C)306 (D)416
答案:(B)
根据《混规》第6.2.17条得
e0=M/N=35×106/150×103=233mm
根据《混规》第6.2.5条得
ea=max(h/30,20)=max(300/30,20)=20mm
根据《混规》式(6.2.17-4)得
ei=e0+ea=233+20=253mm
根据《混规》图6.2.17得
e′=ei-h/2+as′=253-300/2+40=143mm
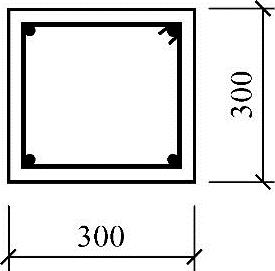
图 3.3.21
(二)偏心受压构件的受力性能
1.大偏心受压与小偏心受压
偏心受压构件随轴向力偏心距的大小和离轴向力远侧纵向钢筋配筋量的不同,存在两种破坏形态,这两种破坏形态的破坏过程、破坏性质是不同的,表3.3.1分析了二种破坏之间的差别。
表3.3.1 偏心受压短柱破坏形态的分析
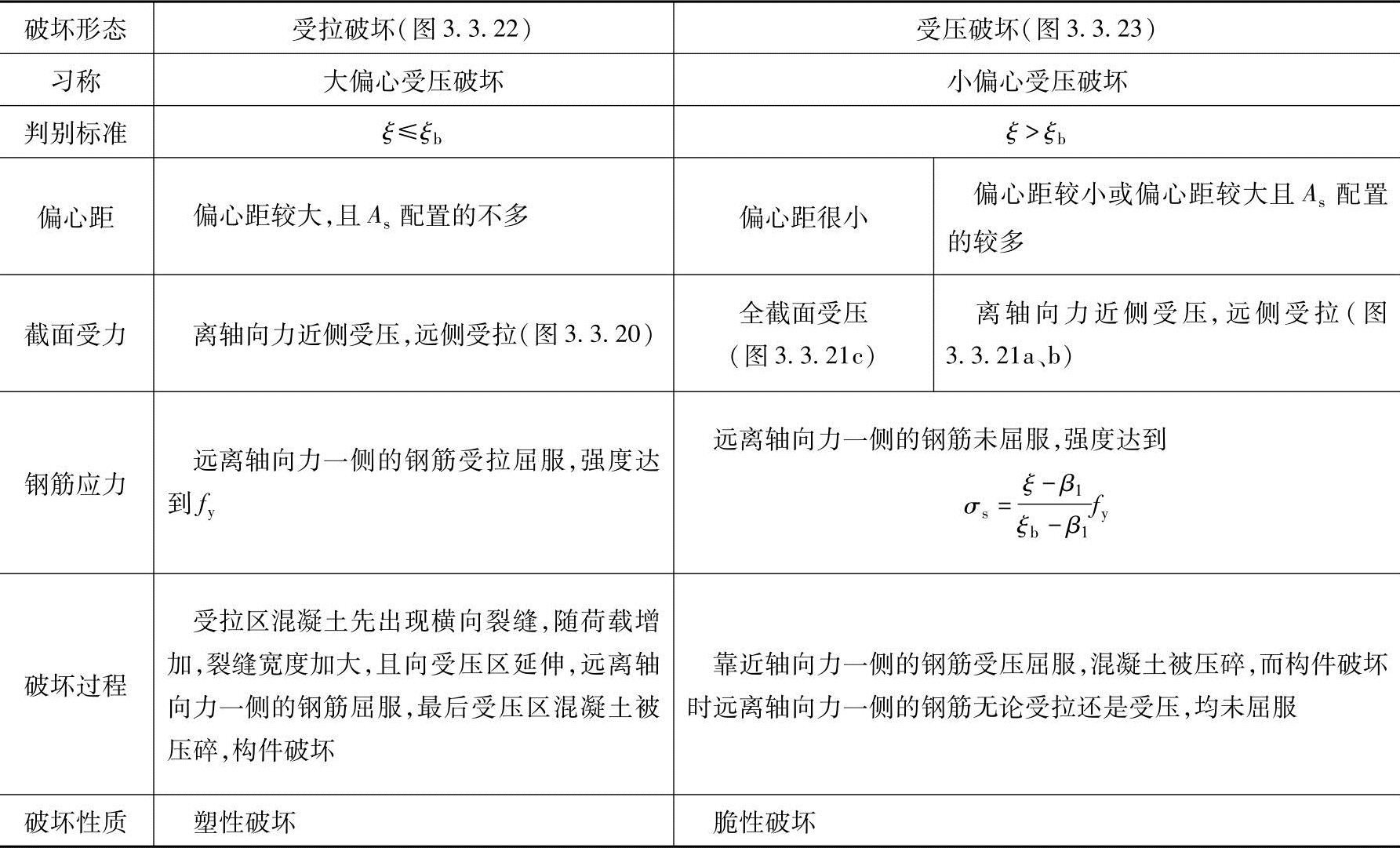
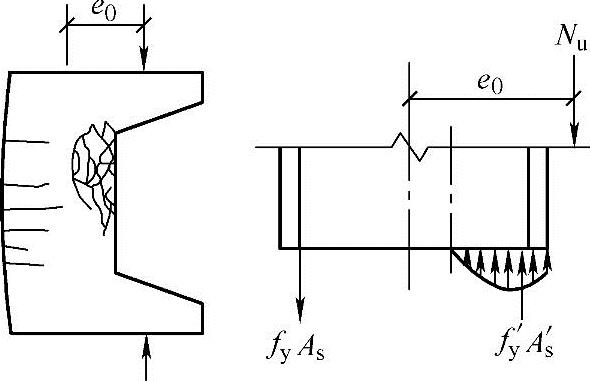
图3.3.22 大偏心受压柱的破坏形态和截面应力分布
图3.3.23 小偏心受压柱的破坏形态和截面应力分布
大偏心受压和小偏心受压构件在发生破坏时,离轴向力较远侧钢筋的应力状态存在着根本的不同。
大偏心受压破坏时,离轴向力较远侧钢筋受拉屈服,其应力达到fy。
小偏心受压破坏时随偏心距大小和离轴向力较远侧钢筋配筋量的不同,使得离轴向力较远侧的钢筋可能受拉也可能受压,但无论受拉还是受压,钢筋均未屈服,其应力为σs。《混凝土结构设计规范》式(6.2.8-3)给出了σs的简化计算方法
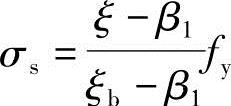
在下列三个界限状态的钢筋应力值分别为:
当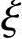 =
=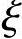 b时,σs=fy;
b时,σs=fy;
当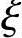 =β1时,σs=0;
=β1时,σs=0;
当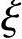 =2β1-
=2β1-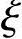 b时,σs=-fy。
b时,σs=-fy。
2.偏心受压柱的Nu-Mu相关曲线
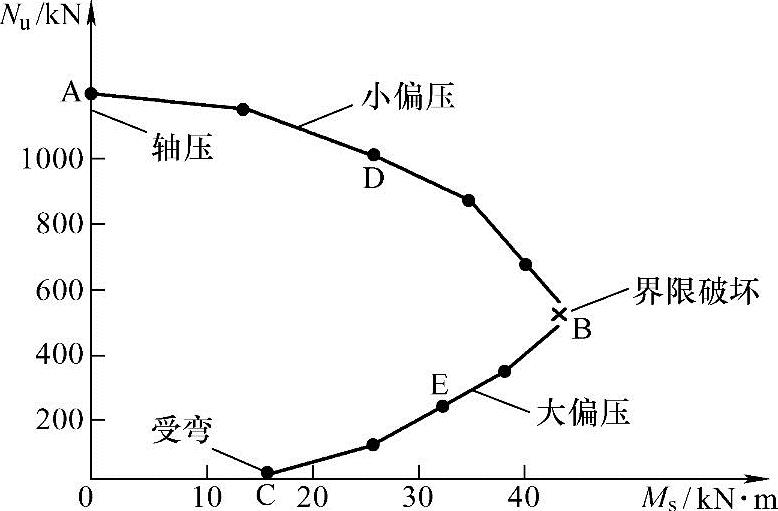
图3.3.24 Nu-Mu试验相关曲线
对于截面尺寸和材料强度确定的偏心受压构件,达到承载力极限状态时,截面承受的Nu和Mu不是相互独立的,而是存在着相关性,即Nu与Mu之间存在一一对应关系。如将一组截面、材料及配筋已知的偏压构件进行试验,可得达到极限状态的Nu和Mu组合。将实验所得的Nu和Mu组合表示在以M为横轴,以N为纵轴的坐标图内,就可以在坐标图内绘出的Nu-Mu相关曲线,如图3.3.24所示。整个曲线分两个曲线段,其中AB曲线为小偏心受压破坏的Nu-Mu曲线,而BC曲线为大偏心受压破坏的Nu-Mu曲线。试验结果表明,在截面、材料及配筋已知的情况下,可以在无数个Nu和Mu组合下达到极限状态。当给定轴力Nu时,在承载能力极限状态下有唯一对应的弯矩Mu。
从N-M相关曲线可以看出,在小偏压破坏时,随着轴向力N的增大,构件的抗弯能力减小;而大偏压破坏时,轴向力N的增大反而会提高构件的抗弯承载力。这主要是因为轴向力在截面上产生的压应力抵消了部分由弯矩引起的拉应力,推迟了受拉破坏的产生。
N-M相关曲线(图3.3.25)反映以下特征:
1)A点坐标(0,Na)是轴心受压承载力;B点坐标(Mb,Nb)是大、小偏心受压的界限点;C点坐标(Mc,0)是受弯构件的承载力。整个曲线段说明了在截面(尺寸、配筋和材料等)一定时,构件从轴心受压到偏心受压,再至受弯的全过程中正截面承载力的变化规律。
2)M=0时,N最大;N=0时,M不是最大;界限破坏B点(Mb,Nb)对应的M最大。
3)大偏心受压时,在某一M值下,N值越大越安全,N值越小越不安全,而需配更多的钢筋;但在小偏心受压时正好相反,在相同的M值下,N值越大越不安全,但无论大偏心受压还是小偏心受压,在某一N值下,M值越大越不安全,M值越小越安全。
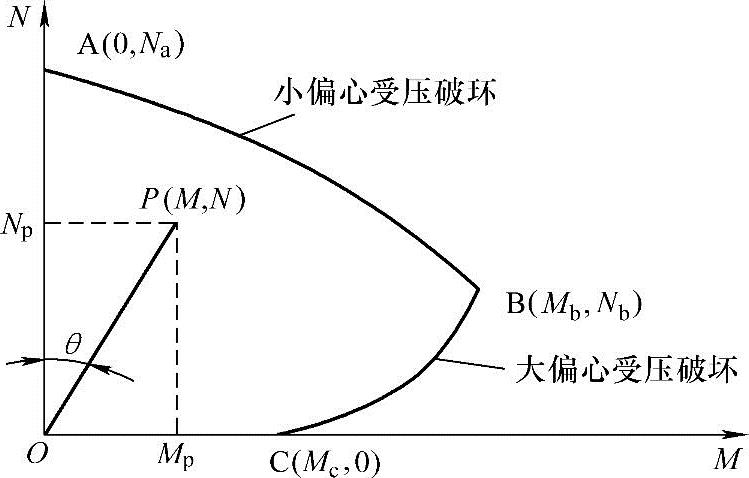
图 3.3.25
N-M相关曲线是偏心受压构件承载能力计算的依据。在坐标系中,任意一点都对应于一组内力P(N,M),如果P点位于曲线与坐标轴围成的区域内(图3.3.25),则说明这样的内力P(N,M)小于截面的承载力,截面不会发生破坏。反之,如果P点位于曲线与坐标轴围成的区域之外时,则说明这样的内力P(N,M)大于截面的承载力,截面将发生破坏;如果P点正好位于曲线上,则说明这样的内力P(N,M)与截面的承载力相等,处于极限状态。
如图3.3.25所示,对于在坐标系中的任意一点P(N,M),OP线与N轴的夹角为θ,tanθ=M/N=e0代表荷载的偏心距。对于理想的偏心受压短柱,在给定的偏心距情况下轴力从零开始,由低到高逐步增加,N和M为线性关系。图3.3.26列出两种偏心距相对值的加载线路图,图中ei/h0较小的直线与小偏压曲线段相交,临界截面的材料达到其极限抗压强度。图中ei/h0较大的直线与大偏压曲线段相交时,临界截面的材料达到其极限抗拉强度。上述情况说明截面发生何类破坏形态是取决于内因和外因的相互影响,其内因即为截面的尺寸、材料及配筋,而外因则为轴压力的大小和偏心距。
3.大、小偏心受压的界限状态
(1)界限破坏时的轴力Nb
当x=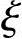 bh0时,为大小偏心受压的界限情况。当构件为矩形截面(图3.3.27),对截面中心取矩,并取as=as′,由截面受力平衡,可得界限破坏时的轴力Nb和弯矩Mb。
bh0时,为大小偏心受压的界限情况。当构件为矩形截面(图3.3.27),对截面中心取矩,并取as=as′,由截面受力平衡,可得界限破坏时的轴力Nb和弯矩Mb。
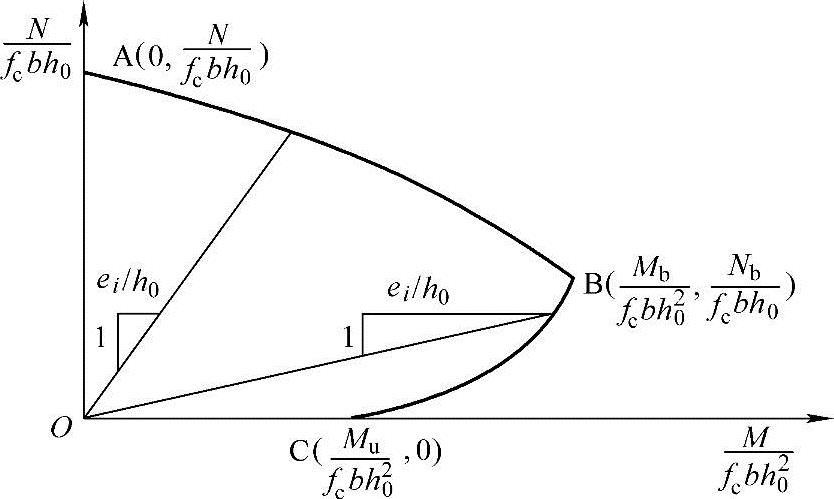
图 3.3.26
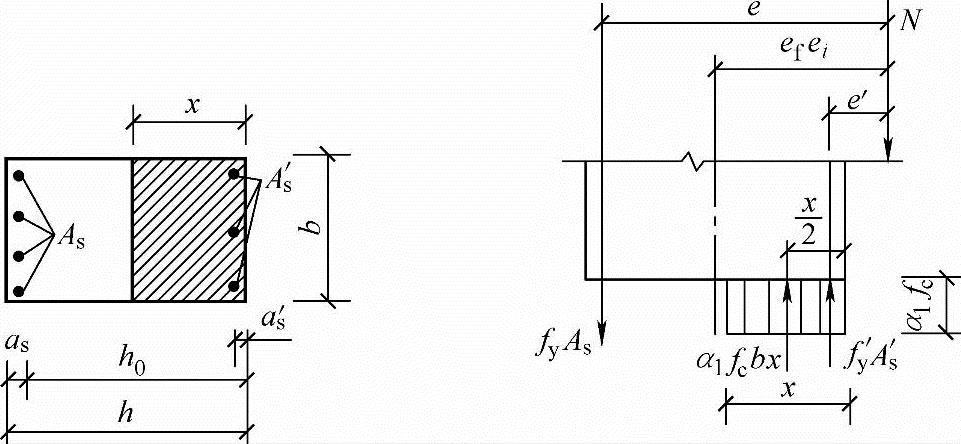
图 3.3.27
Nb=α1fcb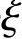 bh0+fy′As′-fyAs (3.3.1)
bh0+fy′As′-fyAs (3.3.1)
Mb=0.5α1fcb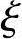 bh0(h-
bh0(h-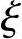 bh0)+0.5(fy′As′+fyAs)(h-2as) (3.3.2)
bh0)+0.5(fy′As′+fyAs)(h-2as) (3.3.2)
当截面尺寸、配筋面积及材料强度为已知时可按式(3.3.1)确定Nb值,如图3.3.28所示,当作用在该截面上的轴向力设计值N≤Nb,为大偏心受压情况;N>Nb则为小偏心受压情况。
(2)界限破坏时的偏心距e0b
由Mb=Nbe0b和式(3.3.1)、式(3.3.2)知:相对界限偏心距e0b/h0(图3.3.29)为
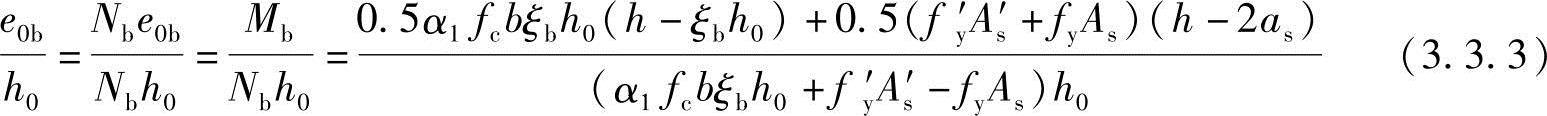
当截面尺寸及材料强度给定时,由上式可知界限偏心距e0b与截面配筋As及As′有关,如As和As′为已知,e0b也是定值。当计算的初始偏心距ei≥e0b时,为大偏心受压情况。当ei<e0b时,为小偏心受压情况。
需要注意的是,由于界限偏心距的公式是针对矩形截面推导出来的,因此它仅适合于矩形截面。
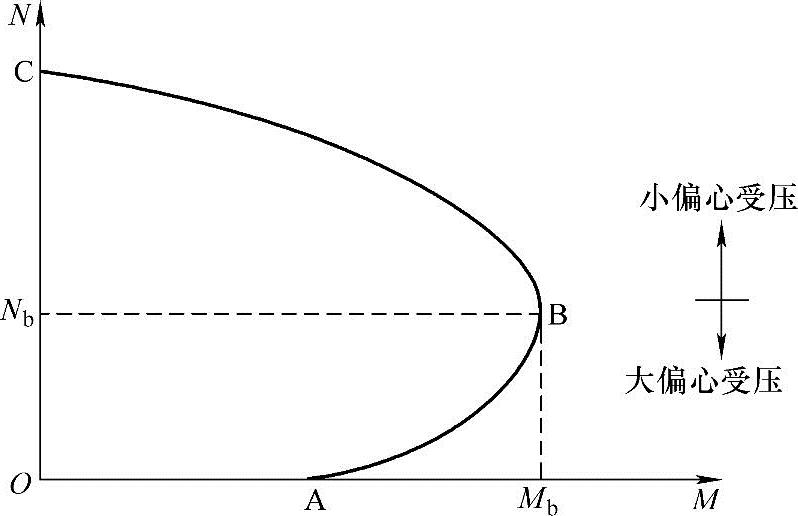
图 3.3.28
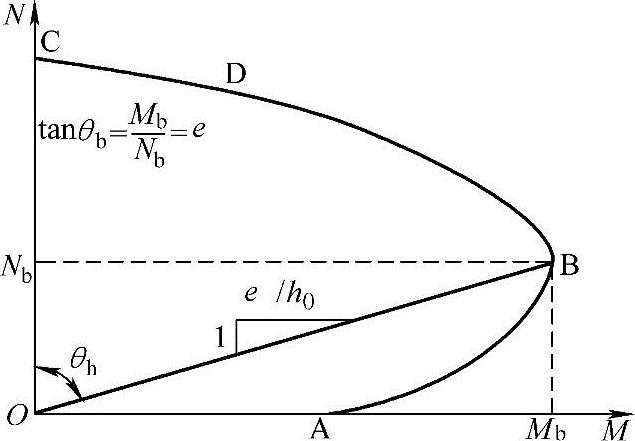
图 3.3.29
4.大小偏心受压的判别
《混凝土结构设计规范》第6.2.17条规定:
1)当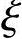 不大于
不大于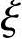 b时为大偏心受压构件,此处,
b时为大偏心受压构件,此处,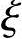 为相对受压区高度,取为x/h0;
为相对受压区高度,取为x/h0;
2)当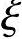 大于
大于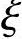 b时为小偏心受压构件。该规定给出了判别大小偏心受压的基本准则,在具体实施时尚可用下列实用方法。
b时为小偏心受压构件。该规定给出了判别大小偏心受压的基本准则,在具体实施时尚可用下列实用方法。
(1)最小的界限偏心距e0b,min
截面配筋计算时,As和As′为未知,因此将无从利用基本公式来计算相对受压区高度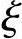 ,所以就不能根据
,所以就不能根据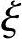 与
与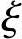 b的比较来判别。为了简化计算,避免进行反复地试算,一种变通的方法是利用式(3.3.3)可以推算出一个最小的界限偏心距e0b,min(即界限偏心距的下限)。当ei≤e0b,min时,必为小偏心受压情况;当ei>e0b,min时,视实际配置的受拉钢筋As的多少可能有两种情况:如实配的As比计算所需的截面面积不过大时,将是受拉钢筋到达fy的大偏心受压情况;如实配的As比计算值大很多时,可能会出现受拉钢筋达不到fy的小偏心受压情况。在截面配筋计算时,由于As为未知或未对As限定任何约束条件(如规定采用对称配筋As=As′),则一般不会出现As过大导致的
b的比较来判别。为了简化计算,避免进行反复地试算,一种变通的方法是利用式(3.3.3)可以推算出一个最小的界限偏心距e0b,min(即界限偏心距的下限)。当ei≤e0b,min时,必为小偏心受压情况;当ei>e0b,min时,视实际配置的受拉钢筋As的多少可能有两种情况:如实配的As比计算所需的截面面积不过大时,将是受拉钢筋到达fy的大偏心受压情况;如实配的As比计算值大很多时,可能会出现受拉钢筋达不到fy的小偏心受压情况。在截面配筋计算时,由于As为未知或未对As限定任何约束条件(如规定采用对称配筋As=As′),则一般不会出现As过大导致的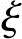 >
>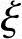 b的情况,故可按大偏心受压情况计算。
b的情况,故可按大偏心受压情况计算。
为了推算出设计中可能有的最小界线偏心距,我们进一步分析式(3.3.3),当截面尺寸和材料强度给定时,界限相对偏心距e0b/h0就取决于截面配筋As和A′s。而随着As和As′的减小,e0b/h0也减小,故当As和As′分别取最小配筋率时,可得e0b/h0的最小值e0b,min/h0。《混凝土结构设计规范》规定,偏心受压构件中,受拉钢筋As按构件全截面面积计算的最小配筋率为0.45ft/fy,受压钢筋As′按构件全截面面积计算的最小配筋率为0.002。近似取h=1.05h0,as′=0.05h0,代入式(3.3.3)中可得对于常用的各种混凝土强度等级和HRB335级、HRB400或RRB400级钢筋,相对界限偏心距的最小值e0b,min/h0=0.248~0.322(表3.3.2)。
表3.3.2 最小相对界限偏心距e0b,min/h0

从上面的分析可知,不对称配筋的偏心受压构件,常用的钢筋为HRB335、HRB400、RRB400级,混凝土强度等级在C20以上时,界限偏心距eb值大致在0.3h0上、下,其平均值可取0.3h0,这样当ei≥0.3h0时,按大偏心受压构件计算;当ei<0.3h0时,按小偏心受压构件计算。
有时虽然符合ei≥0.3h0,属于大偏心受压的条件,但如果在受拉侧配置过多的钢筋,而受压侧的钢筋又配置不足,就有可能出现小偏心受压的情形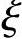 >
>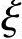 b。此时,可先按大偏心受压破坏进行计算,计算过程中得到
b。此时,可先按大偏心受压破坏进行计算,计算过程中得到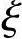 后,再根据
后,再根据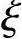 值和
值和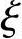 b值的比较结果,最终确定截面属于哪一种破坏形态。
b值的比较结果,最终确定截面属于哪一种破坏形态。
(2)试算法
在截面设计时,先假定构件发生大偏心受压破坏,可根据已知条件直接先按大偏心破坏计算,得到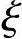 值与
值与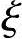 b值比较后确定截面属于哪一种破坏。如
b值比较后确定截面属于哪一种破坏。如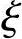 ≤
≤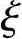 b,则说明原定假设正确,继续进行计算;如
b,则说明原定假设正确,继续进行计算;如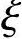 >
>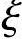 b则说明原定假设错误,改按小偏心重新计算。改按小偏心重新计算所得的
b则说明原定假设错误,改按小偏心重新计算。改按小偏心重新计算所得的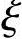 必然满足
必然满足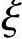 >
>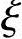 b,但数值上和第一次按大偏心计算所得的
b,但数值上和第一次按大偏心计算所得的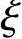 值不同,因为第一次计算所得的
值不同,因为第一次计算所得的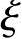 值是根据错误的假定计算得出的。
值是根据错误的假定计算得出的。
本方法的优点可用于任何形状截面的设计计算。
【例3.3.13】 已知轴力、计算压区高度
条件:已知矩形截面偏心受压柱截面尺寸为b×h=450mm×600mm,混凝土强度等级采用C40,纵向钢筋采用HRB400级钢,离轴向力远侧配置4 20(As′=1256mm2),离轴向力近侧配置4
20(As′=1256mm2),离轴向力近侧配置4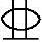 18(As′=1017mm2)。
18(As′=1017mm2)。
要求:(1)求轴向力设计值N=1150kN时的压区高度;
(2)求轴向力设计值N=2700kN时的压区高度。
解答:(1)N=1150kN,先假定构件发生大偏心受压破坏,计算压区高度
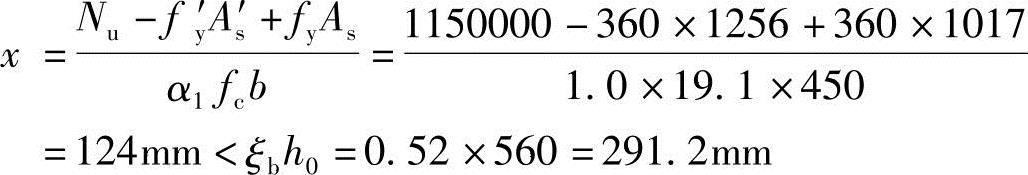
原定假设正确,故为大偏心受压。
(2)N=2700kN,先假定构件发生大偏心受压破坏,计算压区高度
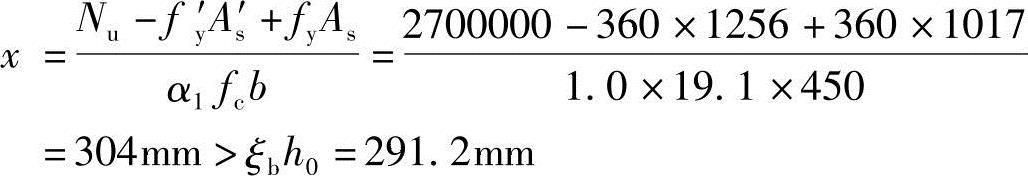
原定假设不正确,故为小偏心受压
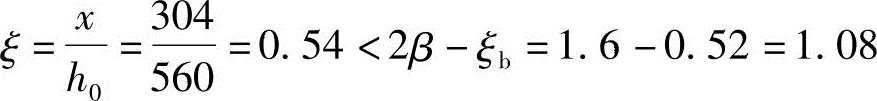
重新求x:
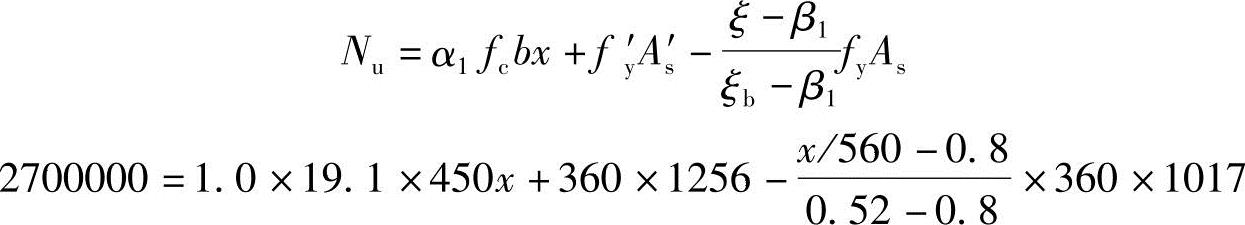
解得:x=301mm
(3)大小偏心受压判别方法的总结
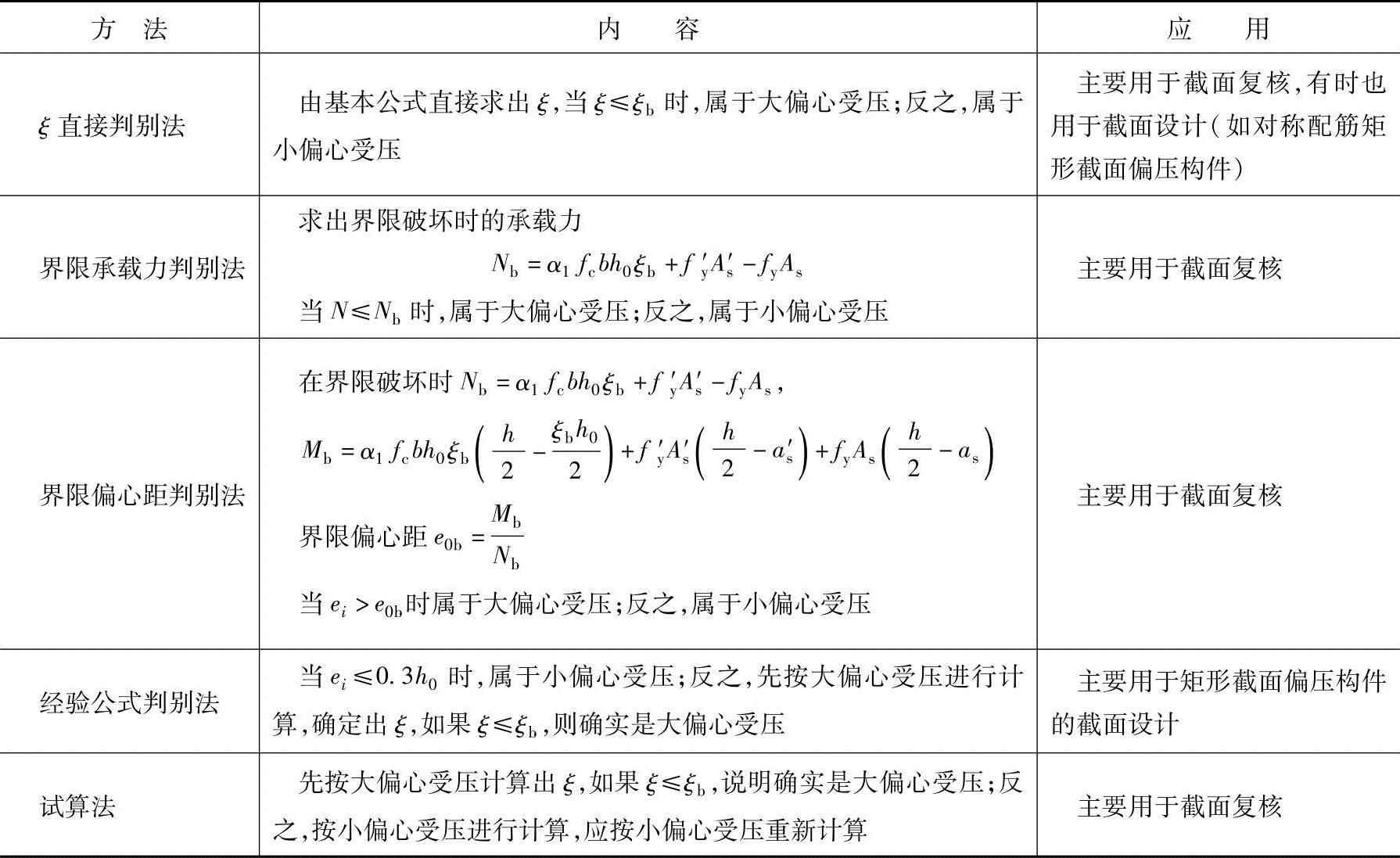
现将判别两类偏心受压的方法汇总于表3.3.3。
表3.3.3 大小偏心受压的判别
5.对称配筋情况下最不利内力组合的确定
当遇到有几组M、N组合时,要进行配筋计算,首先要解决的问题是选择最不利的一组内力。由于大偏心受压和小偏心受压确定最不利内力组合的规律不同,故应分别讨论。
(1)大、小偏心受压的区分
当N>Nb时为小偏心受压;
当N≤Nb时为大偏心受压。
当Nb为界限破坏时的受压承载力
Nb=α1fcbh0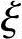 b
b
(2)小偏心受压时的最不利内力组合
从图3.3.30a可以看到,在小偏心受压时,弯矩M和轴力N均为最大的一组内力为最不利。
(3)大偏心受压时的最不利内力组合
从图3.3.30b可以看到,在大偏心受压时,M大、N小的一组内力为最不利。
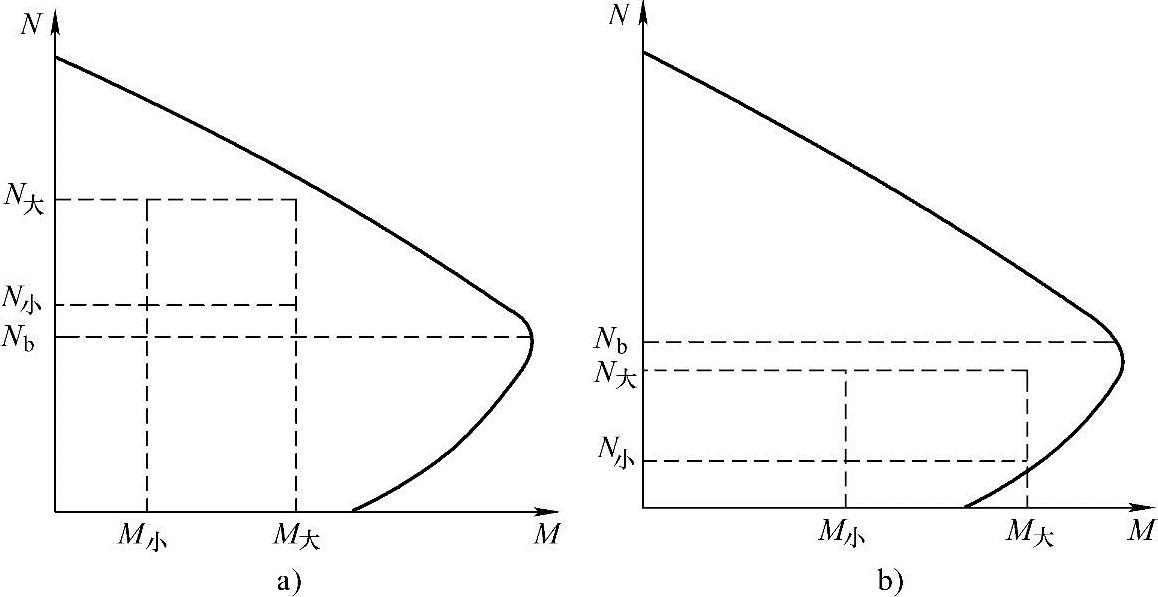
图 3.3.30
a)小偏心受压 b)大偏心受压
【例3.3.14】 最不利内力组合的判断(大偏压)
条件:采用对称配筋的钢筋混凝土大偏心受压柱,在下列四组内力作用下:
(A)M=100kN·m,N=150kN (B)M=100kN·m,N=500kN
(C)M=200kN·m,N=150kN (D)M=200kN·m,N=500kN
要求:试确定由哪一组内力控制配筋。
解答:由Nu-Mu的关系曲线可知大偏心受压破坏时,Nu随Mu的减小而减小,随Mu的增大而增大,界限破坏时的Mu为最大。
根据上述规律,当M相同时,在(A)、(B)中选(A),在(C)、(D)中选(C),当N相同时,在(A)、(C)中选(C)。
【例3.3.15】 最不利内力组合的判断(小偏压)
条件:一钢筋混凝土小偏心受压构件的三组内力分别为

要求:在截面设计时,试确定应采用哪组内力。
解答:应选用M大、N大的一组内力,即采用M=52.1kN·m,N=998kN这一组。
【例3.3.16】 偏压柱截面设计时不利内力的选取
条件:Ⅰ形截面钢混凝土偏心受压柱,截面尺寸为b=100mm,h=700mm,bf=b′f=350mm,hf=hf′=120mm。混凝土强度等级为C25,纵筋采用HRB400级钢筋,对称配筋,as=as′=40mm,相对界限受压区高度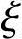 b=0.518。经内力组合得到8组内力设计值,见表3.3.4。
b=0.518。经内力组合得到8组内力设计值,见表3.3.4。
表3.3.4 柱截面内力设计值

要求:配筋计算时应选哪一组或哪几组内力?
答案:由《混规》表4.1.4查得,fc=11.9N/mm2;根据《混规》第6.2.6条,α1=1.0。
Ⅰ形截面对称配筋时,大、小偏心受压界限破坏的轴向力为
Nb=α1fc[bh0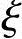 b+(bf′-b)hf′]
b+(bf′-b)hf′]
=1.0×11.9×[100×0.518×660+(350-100)×120]
=763.84kN
当N≤763.84kN时,属于大偏心受压情况;
当N>763.84kN时,属于小偏心受压情况。
根据上述判别条件,表3.3.4中第②、③、④、⑤组为大偏心受压;第①、⑥、⑦、⑧组为小偏心受压。
对大偏心受压组,第②组与第④组比较,应选弯矩大轴力小的第②组;第②组与第⑤组内力比较,可认为轴力相差不多,应选弯矩大的第②组;第②组与第③组比较,弯矩相差较大,轴力相差较小,应选弯矩大的第②组。
对小偏心受压组,第①组与第⑥组比较,应选弯矩大、轴力也大的第①组;第①组与第⑦、⑧组比较,均可认为轴力相差不多,应选弯矩大的第①组。
根据以上分析,应用第②组内力按大偏心受压计算截面配筋,用第①组内力按小偏心受压计算截面配筋,选两者的较大值作为该柱截面配筋。
当按轴心受压构件验算垂直于弯矩作用平面的受压承载力时,应选轴力最大的第⑦组内力。
(三)钢筋混凝土短柱的承载力计算
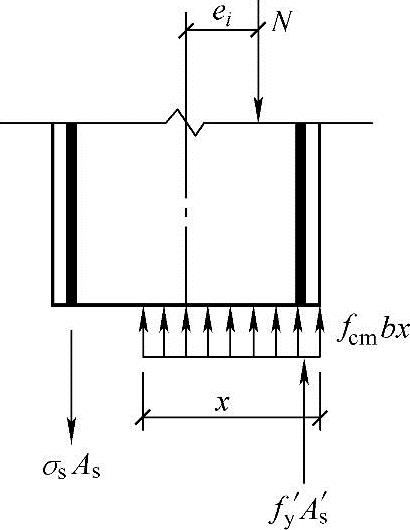
图 3.3.31
1.考试要求
(1)《考试大纲》的要求:掌握
(2)“试题”回顾
【试题3.3.16】 小偏心受压柱所能承受的内力设计值(2002年)
有一承受非恒载为主的钢筋混凝土框架柱。安全等级为Ⅱ级,矩形截面尺寸为b×h=300mm×500mm,对称配筋,每侧各配有3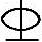 22钢筋(As=942mm2),
22钢筋(As=942mm2),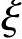 b=0.544,混凝土强度等级为C25,纵向受拉钢筋合力点至截面近边距离as=40mm,该柱的计算长度l0=4.5m。柱正截面受压承载力见图3.3.31,已知该柱为小偏心受压,其轴向力对截面重心的偏心矩e=150mm,受压区高度x=293mm,受拉主筋应力σs=197N/mm2。试问在已给出的配筋量的情况下,该柱所能承受的内力设计值M及N,与下列何项数值最为接近?
b=0.544,混凝土强度等级为C25,纵向受拉钢筋合力点至截面近边距离as=40mm,该柱的计算长度l0=4.5m。柱正截面受压承载力见图3.3.31,已知该柱为小偏心受压,其轴向力对截面重心的偏心矩e=150mm,受压区高度x=293mm,受拉主筋应力σs=197N/mm2。试问在已给出的配筋量的情况下,该柱所能承受的内力设计值M及N,与下列何项数值最为接近?
(A)195kN·m,1300kN (B)222kN·m,1478kN
(C)178kN·m,1186kN (D)194kN·m,1293kN
【试题3.3.17】 大偏压柱的Ne值(2004年)
某钢筋混凝土柱,截面如图3.3.32所示,混凝土强度等级为C40,纵筋采用HRB335级钢筋,对称配筋。已知:as=as′=40mm,fy=fy′=300N/mm2,fc=19.1N/mm2。
已知该柱轴力设计值N=800kN,As=As′=1600mm2,当按大偏心受压构件进行设计时,《混凝土结构设计规范》式(6.2.17-2)右端项(kN·m)与以下何项数值最为接近?
(A)527.68 (B)372.54
(C)624.25 (D)602.37
2.《混凝土结构设计规范》规定与讨论
《混凝土结构设计规范》规定:
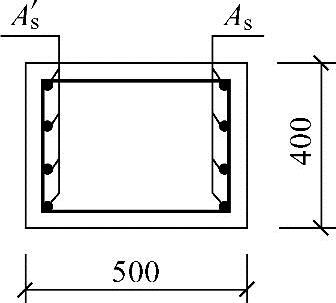
图 3.3.32
6.2.17 矩形截面偏心受压构件正截面受压承载力应符合下列规定(图6.2.17):
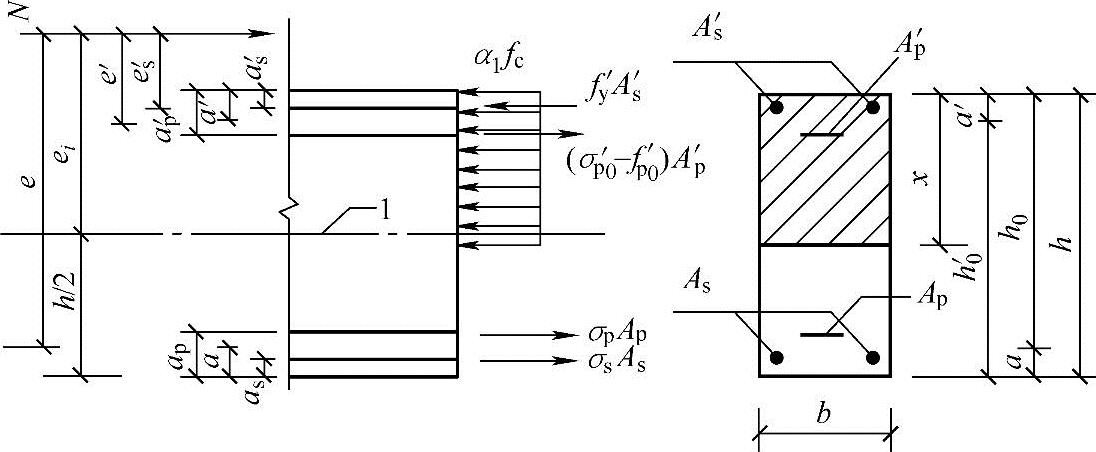
图6.2.17 矩形截面偏心受压构件正截面受压承载力计算
1—截面重心轴
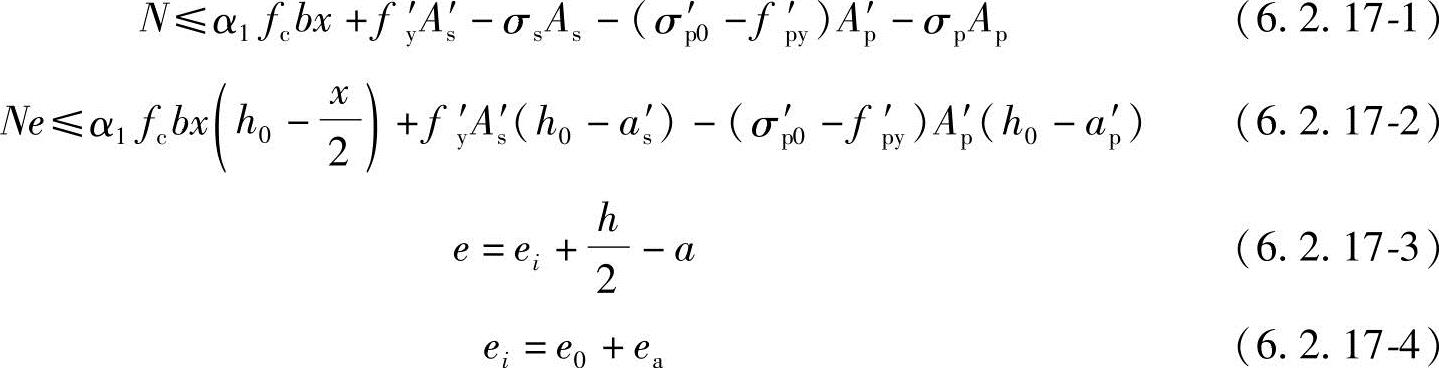
式中 e——轴向压力作用点至纵向受拉普通钢筋和受拉预应力筋的合力点的距离;
σs、σp——受拉边或受压较小边的纵向普通钢筋、预应力筋的应力;
ei——初始偏心距;
a——纵向受拉普通钢筋和受拉预应力筋的合力点至截面近边缘的距离;
e0——轴向压力对截面重心的偏心距,取为M/N;
ea——附加偏心距,按本规范第6.2.5条确定。
(1)大偏心受压情况(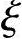 ≤
≤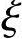 b)
b)
大偏心受压破坏时截面的计算应力图形如图3.3.33所示。
根据大偏压的计算应力图形可将《混凝土结构设计规范》中的式(6.2.17-1)、式(6.2.17-2)直接写成下列表达式。
N≤Nu=α1fcbx+fy′As′-fyAs
Ne≤Nue=α1fcbx(h0-0.5x)+fy′As′(h0-as′)
为了保证截面破坏时受拉钢筋应力达到其抗拉强度设计值,必须满足下列条件:
x≤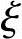 bh0
bh0
或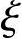 ≤
≤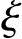 b
b
为了保证截面破坏时受压钢筋应力达到屈服强度,还须满足《混凝土结构设计规范》第6.2.17条2款的规定。
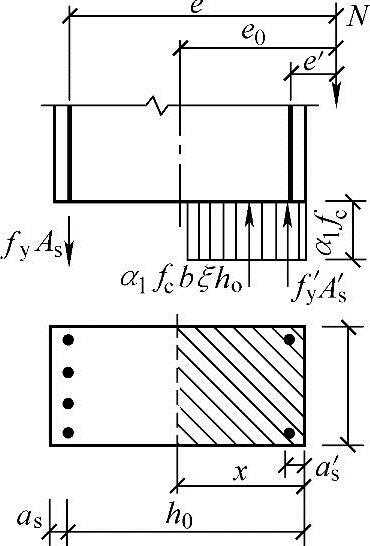
图3.3.33 大偏心受压破坏计算简图
6.2.17
2.当计算中计入纵向受压普通钢筋时,受压区高度应满足本规范式(6.2.10-4)的条件:当不满足此条件时,其正截面受压承载力可按本规范第6.2.14条的规定进行计算,此时,应将本规范式(6.2.14)中的M以Nes′代替,此处,es′为轴向压力作用点至受压区纵向普通钢筋合力点的距离;初始偏心距应按式(6.2.17-4)确定。
即必须满足下列条件:
x≥2a′
或 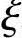 h0≥2as′
h0≥2as′
若不满足上述条件,则与双筋受弯构件一样,取受压区高度x=2as′,并对受压钢筋重心取矩(图3.3.34),即得《混凝土结构设计规范》式(6.2.14)的表达式:
Ne′=Nue′=fyAs(h0-as′)
e′=ei-h/2+as′
(2)小偏心受压情况(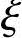 >
>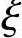 b)
b)
小偏心受压破坏时,距轴向压力较近一侧混凝土达到极限压应变,受压钢筋中的应力σs′值达到抗压强度设计值fy′,而另一侧钢筋中的应力值不论是受压还是受拉均未达到其强度设计值,即σs<fy′(或fy)。截面应力图形如图3.3.35所示。
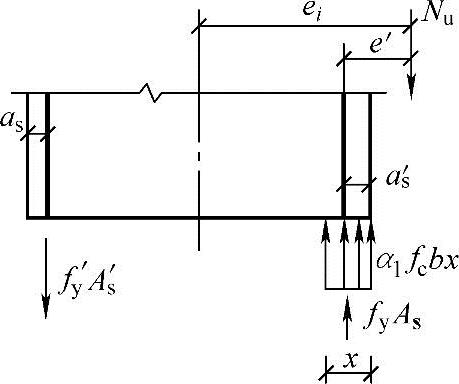
图 3.3.34
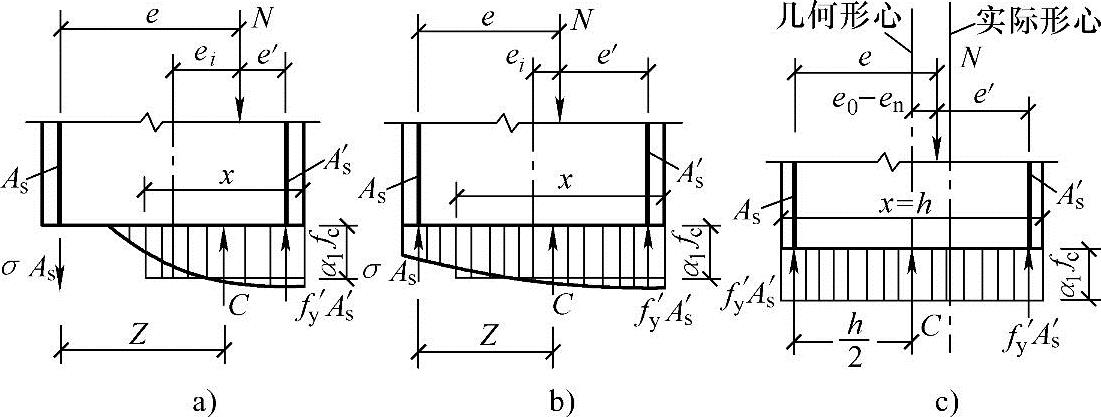
图3.3.35 小偏心受压破坏计算简图
根据力的平衡条件和力矩平衡条件,《混凝土结构设计规范》式(6.2.17-1)、式(6.2.17-
2)能用下式表达
∑Y=0,N≤Nu=α1fcbx+fy′As′-σsAs (3.3.4)
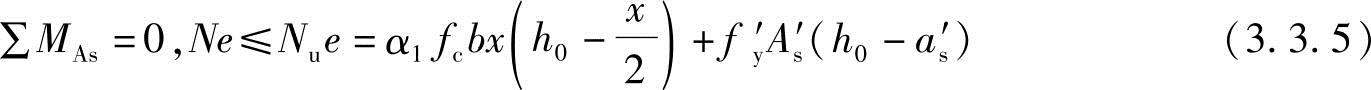
或 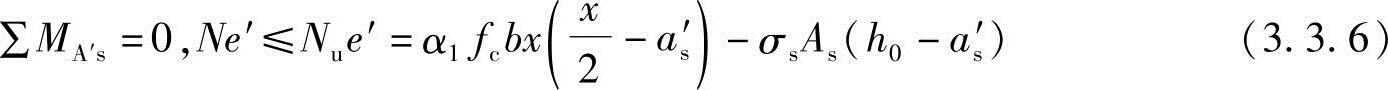
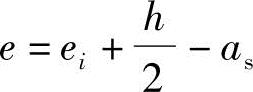
应当指出,对于轴向压力作用点靠近截面重心的小偏心受压构件,当As′比As大得多,且轴力很大时,截面实际形心轴偏向A′s一边,以致轴向力的偏心改变了方向。因此,有可能在离轴向力较远的一侧混凝土先被压坏,这种情况称为反向破坏(图3.3.33c)。为了防止这种反向破坏的发生,必须满足《混凝土结构设计规范》第6.2.17条3款的规定。
6.2.17
3.矩形截面非对称配筋的小偏心受压构件,当N大于fcbh时,尚应按下列公式进行验算:
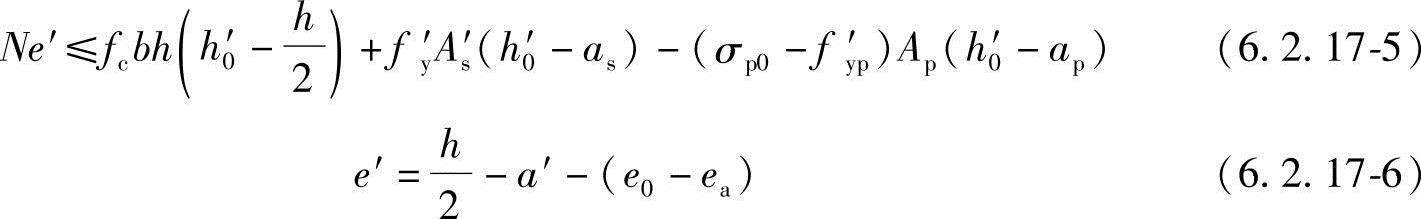
式中 e′——轴向压力作用点至受压区纵向普通钢筋和预应力筋的合力点的距离;
h0′——纵向受压钢筋合力点至截面远边的距离。下列表达式是对称配筋小偏心受压柱的承载力计算公式:
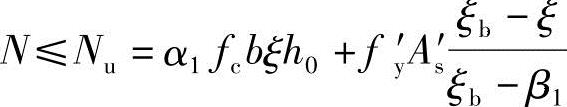
Ne≤Nue=α1fcbh20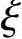 (1-0.5
(1-0.5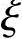 )+fy′As′(h-as′)
)+fy′As′(h-as′)
应用上述公式求解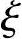 值要解三次方程,计算相当复杂,《混凝土结构设计规范》第6.2.17条第4款给出一个十分简单的近似计算公式。
值要解三次方程,计算相当复杂,《混凝土结构设计规范》第6.2.17条第4款给出一个十分简单的近似计算公式。
6.2.17
4.矩形截面对称配筋(As′=As)的钢筋混凝土小偏心受压构件,也可按下列近似公式计算纵向普通钢筋截面面积:
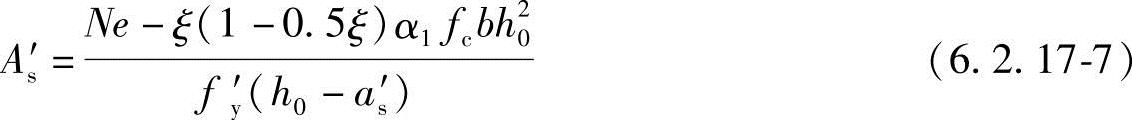
此处,相对受压区高度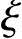 可按下列公式计算:
可按下列公式计算:
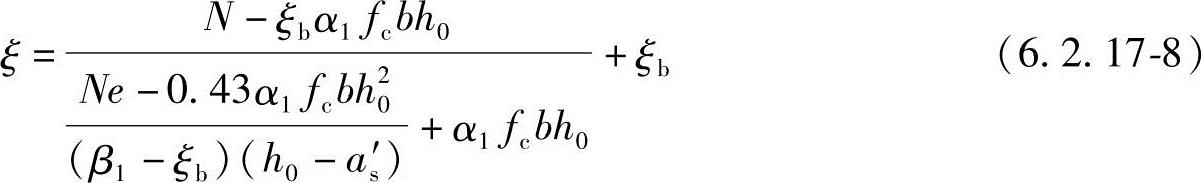
3.《混凝土结构设计规范》规定的应用
对称配筋是指Asfy=As′fy′。对HRB500、HRBF500级钢筋,fy=435N/mm2,fy′=410N/mm2,虽As=As′,但Asfy≠As′fy′,此时不能按对称配筋计算,仍按非对称配筋计算。
(1)矩形截面对称配筋偏压构件的配筋计算
基本资料:已知截面尺寸b、h、材料强度fc、ft、fy;外部荷载效应M、N。
确定需用的计算参数α1、β1、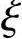 b、as、as′、h0。
b、as、as′、h0。
计算步骤:
1)确定初始偏心距ei
根据《混凝土结构设计规范》第6.2.17条,取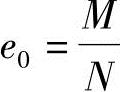 ;
;
根据《混凝土结构设计规范》第6.2.5条ea=max(20mm,h/30);
根据《混凝土结构设计规范》式(6.2.17-4),ei=e0+ea。
2)求轴向力到纵向钢筋作用点的距离e(e′)
根据《混凝土结构设计规范》式(6.2.17-3),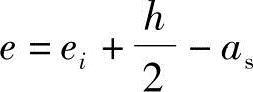 ;
;
根据《混凝土结构设计规范》图6.2.17,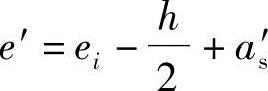 。
。
3)求混凝土受压区高度
由《混凝土结构设计规范》式(6.2.17-1),N<α1fcbx,取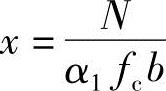
①当x≤ bh0时,即采用
bh0时,即采用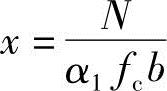 ;
;
②当x>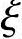 bh0时,根据《混凝土结构设计规范》式(6.2.17-8):
bh0时,根据《混凝土结构设计规范》式(6.2.17-8):
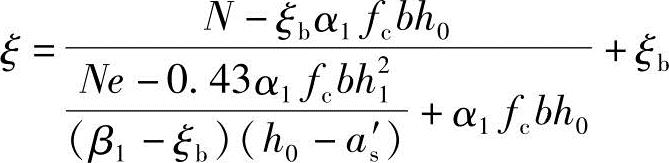
4)求纵向钢筋As=As′
①当x<2as′时,根据《混凝土结构设计规范》式(6.2.14)得
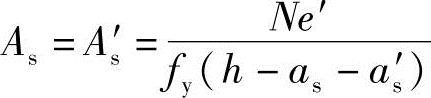
②当x≥2as′时,根据《混凝土结构设计规范》式(6.2.17-2)得
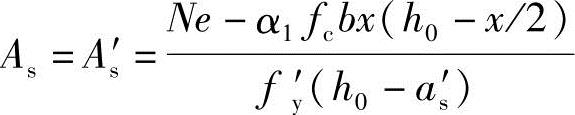
③当xb≥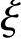 bh0时,根据《混凝土结构设计规范》式(6.2.17-2),此时取x=
bh0时,根据《混凝土结构设计规范》式(6.2.17-2),此时取x=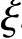 h0可知
h0可知
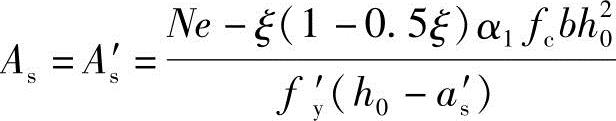
5)验算每一侧纵向钢筋的最小配筋率
根据《混凝土结构设计规范》表8.5.1,当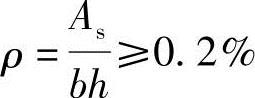 时通过,否则要调整。
时通过,否则要调整。
6)验算全部纵向钢筋的最小配筋率
根据《混凝土结构设计规范》表8.5.1,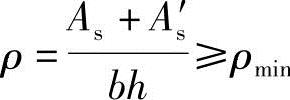 时通过,否则要调整。
时通过,否则要调整。
强度等级为500MPa时, ρmin=0.50%
强度等级为400MPa时, ρmin=0.55%
强度等级为300MPa、335MPa时, ρmin=0.60%
7)验算全部纵向钢筋的最大配筋率
根据《混凝土结构设计规范》第9.3.1条1款,当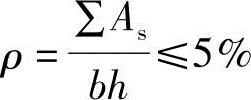 时通过,否则要调整。
时通过,否则要调整。
【例3.3.17】 纵向钢筋截面面积As=As′(2as′>x)
条件:钢筋混凝土框架柱,截面尺寸为b×h=400mm×450mm,as=a′s=40mm。承受轴向压力设计值N=320kN,柱端弯矩设计值M=300kN·m。混凝土强度等级为C30(fc=14.3N/mm2),采用HRB400级钢筋(fy=fy′=360N/mm2),采用对称配筋。
提示:本题所讨论的框架柱为短柱,不考虑长细比影响。
要求:求纵向钢筋截面面积As=As′。
解答:基本资料:根据《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条、8.2.1条,可知fc=14.3N/mm2,ft=1.43N/mm2,fy=fy′=360N/mm2,α1=1, b=0.518,c=20mm取as=as′=40,h0=h-as=450-40=410mm。
b=0.518,c=20mm取as=as′=40,h0=h-as=450-40=410mm。
(1)确定初始偏心距
由《混规》第6.2.17条:
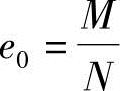 可得
可得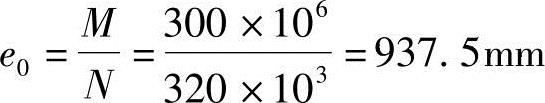
根据《混规》第6.2.5条ea=max(20mm,h/30):
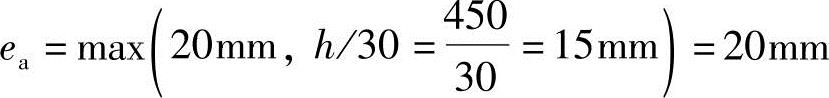
根据《混规》式(6.2.17-4)ei=e0+ea可得
ei=e0+ea=937.5+20=957.5mm
(2)求轴向力到纵向钢筋作用点的距离
根据《混规》式(6.2.17-3)e=ei+h/2-as和图6.2.17中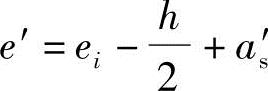 可得
可得
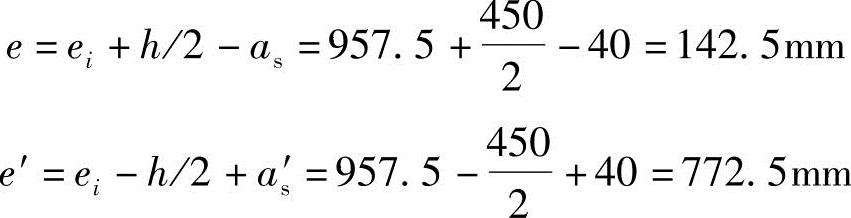
(3)求混凝土压区高度,并验算压区高度
取
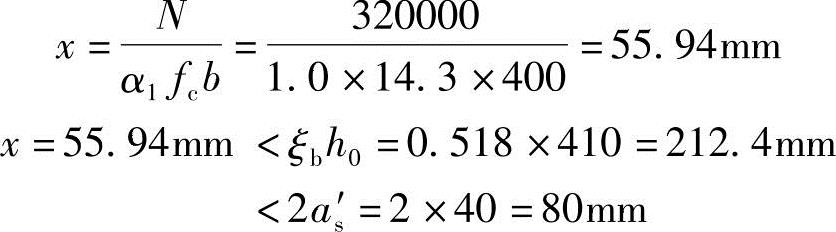
(4)求纵向钢筋As和As′
当x≤2as′,根据《混规》式(6.2.14):
M≤fyAs(h-as-as′)
可得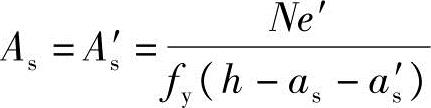 ,代入相关数据可得
,代入相关数据可得
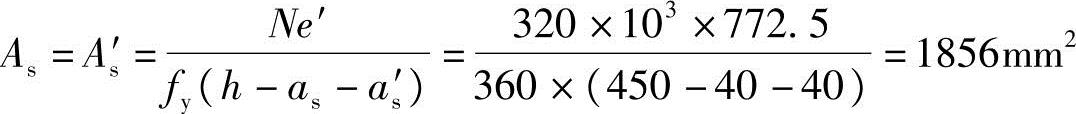
(5)验算每一侧纵向钢筋的最小配筋率
根据《混规》表8.5.1,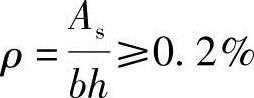 得
得
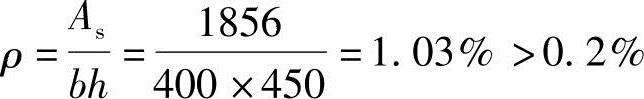
(6)验算纵向钢筋的最小配筋率
根据《混规》第8.5.1条:
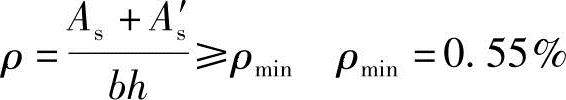
截面每侧各配置4 25(As=1964mm2)配筋,如图3.3.36所示。
25(As=1964mm2)配筋,如图3.3.36所示。
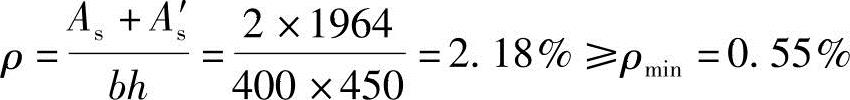
(7)验算纵向钢筋最大配筋率
根据《混规》第9.3.1条1款
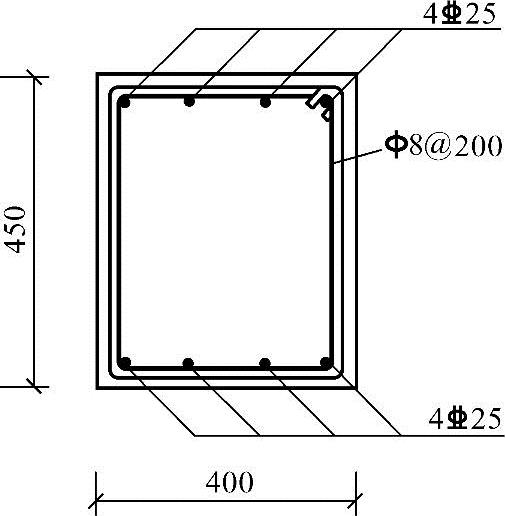
图 3.3.36
ρmax≤5%ρ=2.18%<5%
【例3.3.18】 纵向钢筋截面面积As=As′(2as′<x<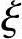 b)
b)
条件:钢筋混凝土框架柱,截面尺寸为b×h=400mm×450mm,as=a′s=40mm。承受轴向压力设计值N=480kN,柱端弯矩设计值M=368.2kN·m。混凝土强度等级为C30(fc=14.3N/mm2),采用HRB400级钢筋(fy=fy′=360N/mm2),采用对称配筋。
提示:本题所讨论的框架柱为短柱,不考虑长细比影响。
要求:求纵向钢筋截面面积As=As′。
解答:基本资料:根据《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条、8.2.1条,可知fc=14.3N/mm2,ft=1.43N/mm2,fy=fy′=360N/mm2,α1=1.0,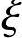 b=0.518,h0=h-as=450-40=410mm
b=0.518,h0=h-as=450-40=410mm
(1)确定初始偏心距
由《混规》第6.2.17条,e0=M/N可得
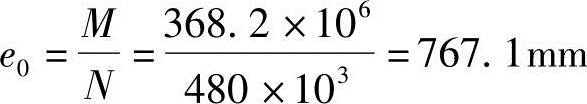
由《混规》第6.2.5条,ea=max(20mm,h/30):
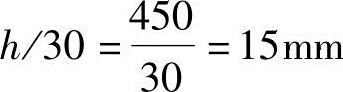 所以ea=20mm
所以ea=20mm
根据《混规》式(6.2.17-4),ei=e0+e0可得
ei=e0+ea=767.1+20=787.1mm
(2)轴向力到纵向钢筋作用点的距离e(或e′)
根据《混规》式(6.2.17-3),可得
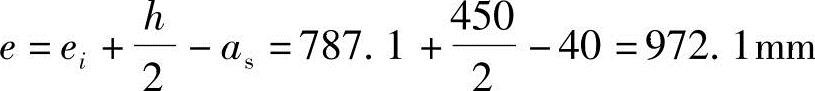
(3)求混凝土压区高度x,并验算压区高度是否满足《混规》式(6.2.10-3-4),
取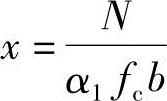 可得
可得
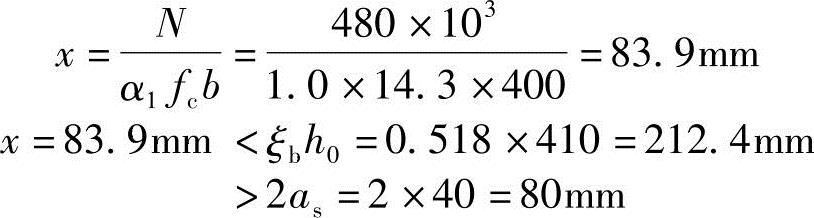
(4)求纵向受力钢筋As、As′
根据《混规》式(6.2.17-2)得
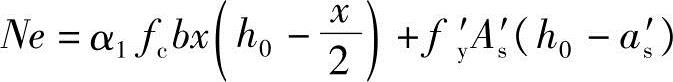
可得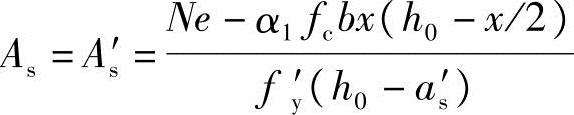 ,代入已知条件可得
,代入已知条件可得
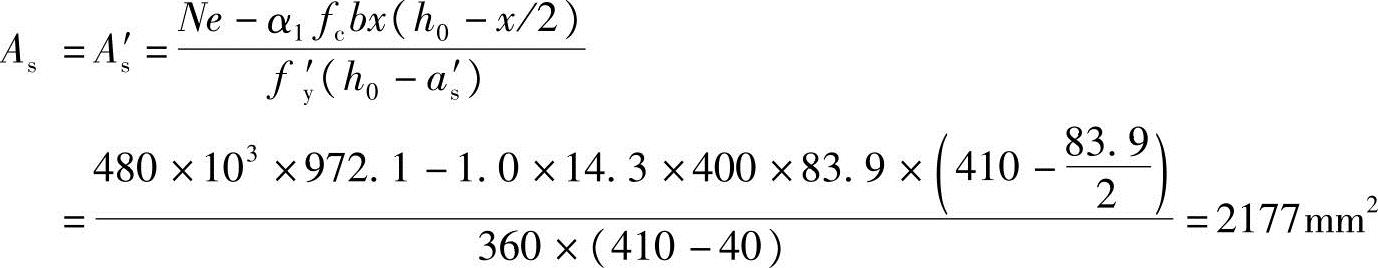
(5)验算每一侧纵向钢筋的最小配箍率
根据《混规》表8.5.1,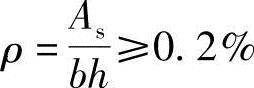

(6)验算全部纵筋的最小配筋率
根据《混规》表8.5.1,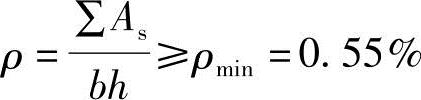
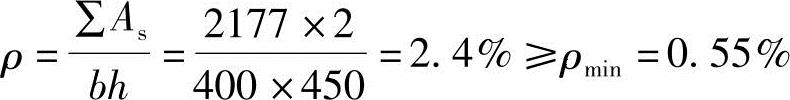
(7)验算全部纵筋的最大配筋率
根据《混规》第9.3.1条第1款:
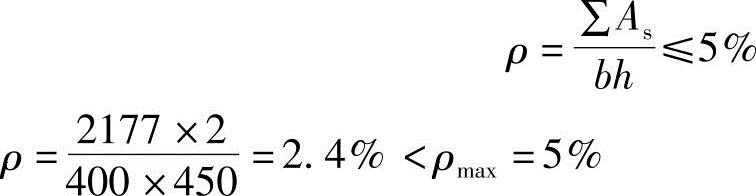
(8)配筋
截面每侧各配置2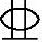 22+3
22+3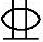 25(As=2233mm2),配筋如图3.3.37所示。
25(As=2233mm2),配筋如图3.3.37所示。
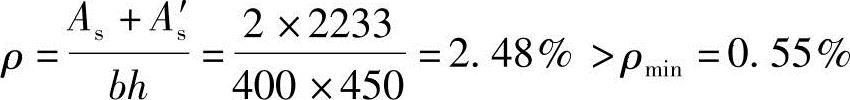
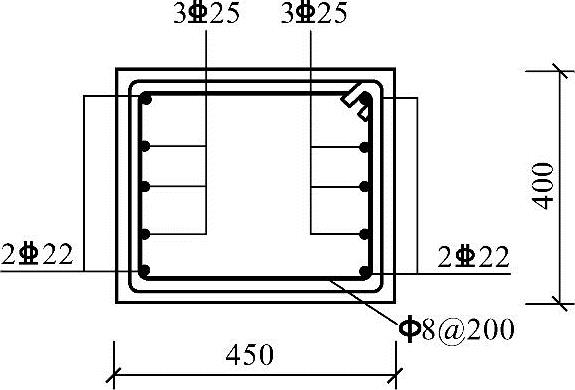
图 3.3.37
【例3.3.19】 纵向钢筋截面面积As=As′(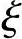 >
>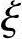 b)
b)
条件:钢筋混凝土框架柱,截面尺寸为b×h=400mm×600mm,as=a′s=40mm。承受轴向压力设计值N=2500kN,柱端弯矩设计值M=98.11kN·m。混凝土强度等级为C25(fc=11.9N/mm2),采用HRB400级钢筋(fy=fy′=360N/mm2),采用对称配筋。
提示:本题所讨论的框架柱为短柱,不考虑长细比影响。
要求:求纵向钢筋截面面积As=As′。
解答:基本资料:根据《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条、8.2.1条,可知fc=11.9N/mm2,fy=fy′=360N/mm2,α1=10,β1=0.8,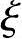 b=0.518,as=as′,h0=h0-as=600-40=560mm。
b=0.518,as=as′,h0=h0-as=600-40=560mm。
(1)确定初始偏心距ei
由《混规》第6.2.17条,e0=M/N可得:
e0=M/N=98.11×106/2500×103=39.24mm
由《混规》第6.2.5条,取ea=max(20,h/30)较大值
h/30=600/30=20mm取ea=20mm
由《混规》式(6.2.17-4),ei=e0+ea可得:
ei=e0+ea=39.24+20=59.24mm
(2)求轴向力到纵向钢筋作用点的距离e或e′
根据《混规》式(6.2.17-3),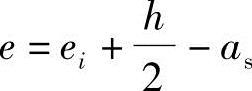 得:
得:
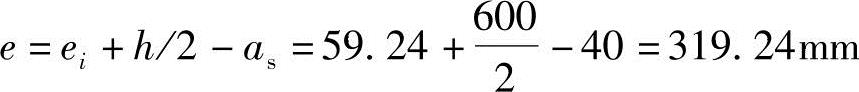
(3)求压区高度x,并验算x是否满足《混规》式(6.2.10-3)、式(6.2.10-4)要求。
取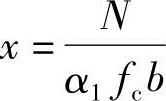 可得:
可得:
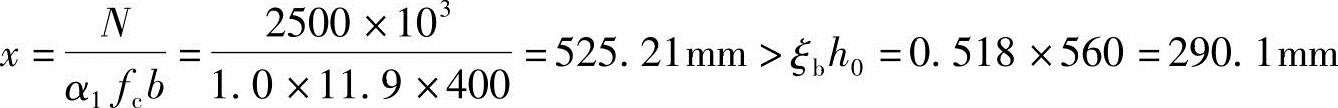
根据《混规》式(6.2.17-8)得:
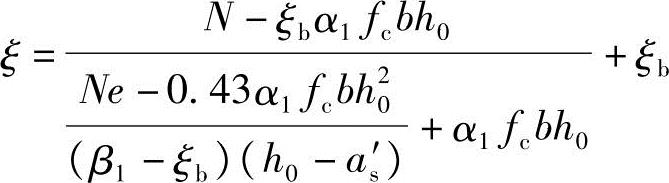
代入已知条件可得:
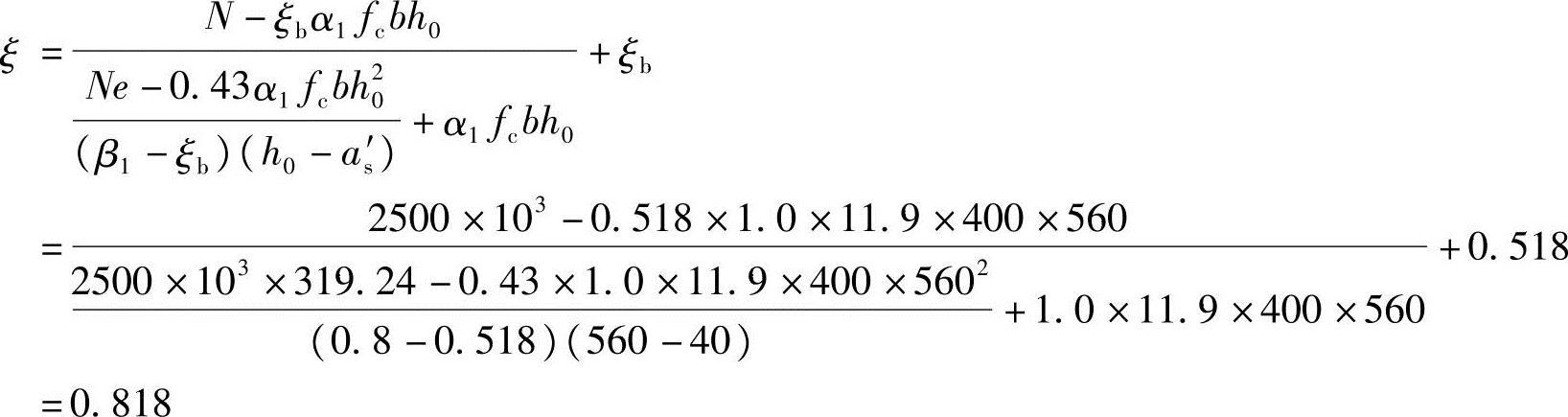
(4)求纵向钢筋As=As′
根据《混规》式(6.2.17-2)得:
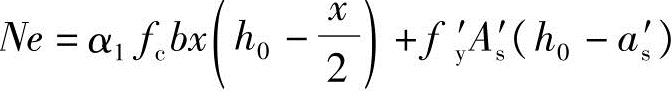
此处x=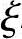 h0代入可得:
h0代入可得:
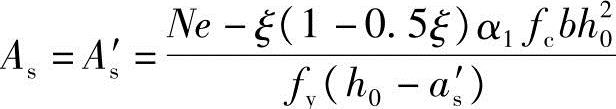
代入已知条件:
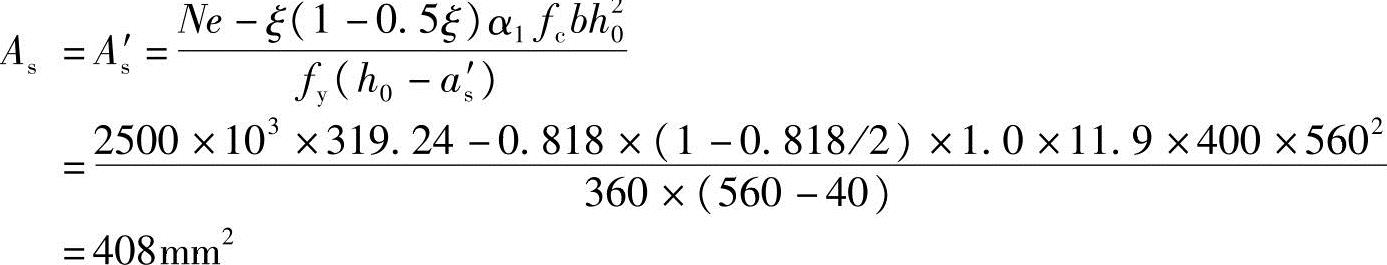
(5)验算每一侧纵向钢筋的最小配箍率
根据《混规》表8.5.1,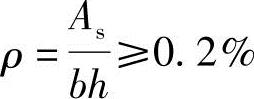
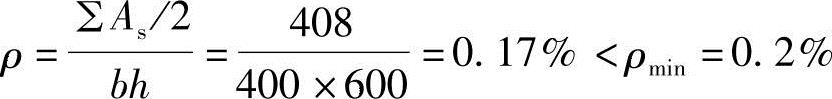
As,min=0.002bh=480mm2,选4 16,即As=804mm2
16,即As=804mm2
(6)验算全部纵筋的最小配筋率
根据《混规》表8.5.1,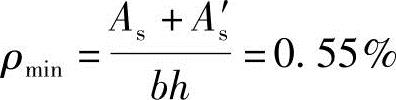
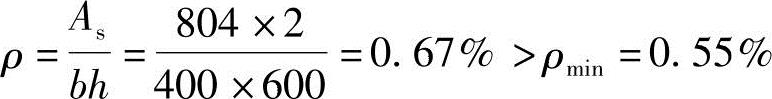
(7)验算全部纵筋的最大配筋率
根据《混规》第9.3.1条第1款,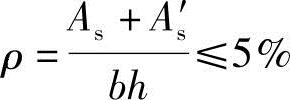
ρ=0.67%<ρmax=5%
(8)配筋
截面每侧各配置4 16(As=804mm2),配筋如图3.3.38所示。
16(As=804mm2),配筋如图3.3.38所示。
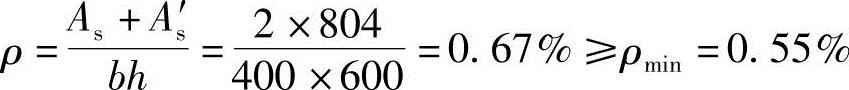
(2)矩形截面对称配筋大偏压构件的承载力计算
1)已知N,求M
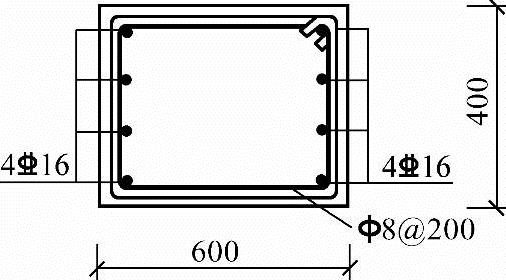
图 3.3.38
基本资料:已知截面尺寸b、h,纵向钢筋截面面积As=As′,材料强度fc、ft、fy;外部荷载效应N。
确定需用的计算参数α1、β1、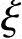 b、as、as′、h0。
b、as、as′、h0。
计算步骤:
①验算配筋率
a.验算每一侧纵向钢筋的最小配筋率根据《混凝土结构设计规范》表8.5.1,当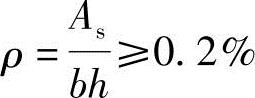 时通过,否则本题不成立。
时通过,否则本题不成立。
b.验算全部纵向钢筋的最小配筋率
根据《混凝土结构设计规范》表8.5.1,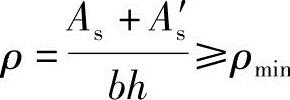 时通过,否则本题不成立。
时通过,否则本题不成立。
当钢筋强度等级为500MPa时, ρmin=0.50%
当钢筋强度等级为400MPa时, ρmin=0.55%
当钢筋强度等级为300MPa、335MPa时, ρmin=0.60%
c.验算全部纵向钢筋的最大配筋率
根据《混凝土结构设计规范》第9.3.1条第1款,当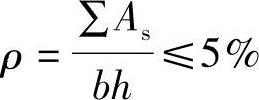 时通过,否则本题不成立。
时通过,否则本题不成立。
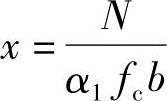
②求混凝土受压区高度x值。并验算压区高度x是否满足《混凝土结构设计规范》式(6.2.10-3)、式(6.2.10-4)要求。
③求轴向压力作用点到纵向钢筋合力点的距离e(或e′)
a.当x<2as′时,根据《混凝土结构设计规范》式(6.2.14)得到
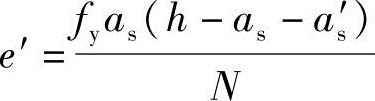 ,转入④中ab.当x≥2as′时,根据《混凝土结构设计规范》式(6.2.17-2)得到
,转入④中ab.当x≥2as′时,根据《混凝土结构设计规范》式(6.2.17-2)得到
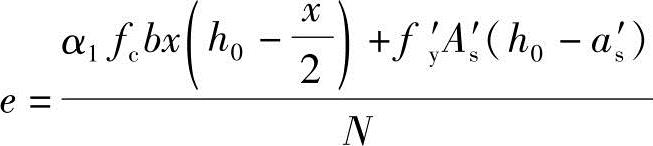 ,转入④中b
,转入④中b
④求初始偏心距ei
a.根据《混凝土结构设计规范》图6.2.17,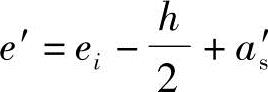 ,得到
,得到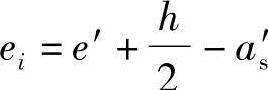 ;
;
b.根据《混凝土结构设计规范》式(6.2.17-3),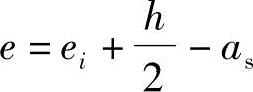 ,得到
,得到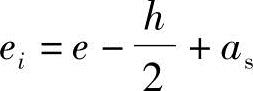 。
。
⑤求轴向力对截面重心的偏心距e0
根据《混凝土结构设计规范》式(6.2.17-4),得到e0=ei-ea;
根据《混凝土结构设计规范》第6.2.5条得
e0=max(20mm,h/30)
⑥求M
根据《混凝土结构设计规范》第6.2.17条,e0=M/N
M=Ne0
【例3.3.20】 偏压柱的承载力计算,已知N求M(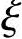 <2as′/h0)
<2as′/h0)
条件:已知一钢筋混凝土偏心受压柱截面尺寸为b×h=400mm×500mm,柱子的计算长度为l0=4.0m,混凝土强度等级为C30,纵向钢筋采用HRB400,对称配置纵向钢筋为5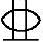 20,As=As′=1570mm2,柱子上作用轴向力设计值为400kN。安全等级二级、环境类别一类。
20,As=As′=1570mm2,柱子上作用轴向力设计值为400kN。安全等级二级、环境类别一类。
提示:本题所讨论的柱为短柱,不考虑长细比影响。
要求:求该柱能承受的弯矩设计值M。
解答:查《混规》表8.2.1知该柱的保护层厚度c=20mm,取as=40mm=as′。h0=h-as=500-40=460mm
查《混规》表4.1.4得fc=14.3N/mm2,ft=1.43N/mm2;
查《混规》表4.2.3-1得fy=fy′=360N/mm2;
查《混规》第6.2.6条,得α1=1.0;
按《混规》式(6.2.7)计算得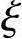 b=0.518。
b=0.518。
(1)验算每一侧纵向钢筋的最小配筋率
根据《混规》表8.5.1,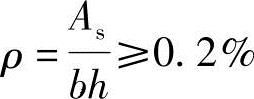
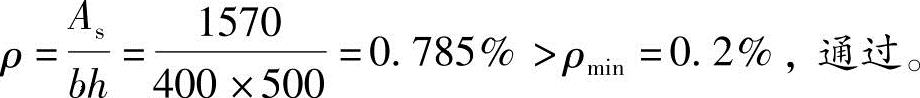
(2)验算全部纵向钢筋的最小配筋率
根据《混规》表8.5.1,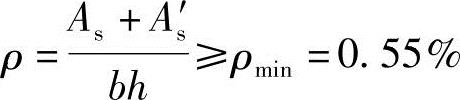
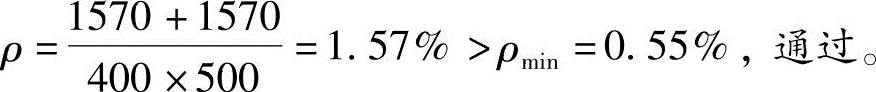
验算全部纵向钢筋的最大配筋率
根据《混规》第9.3.1条第1款,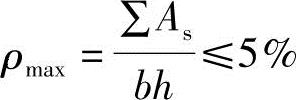
ρ=1.57%≤ρmax=5%,通过。
(3)求混凝土压区高度x
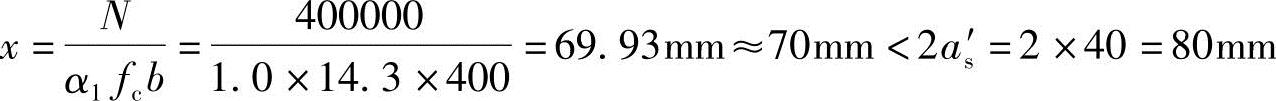
(4)求轴向压力作用点到纵向钢筋合力点距离e(或e′)
x=70mm<2as′=2×40=80mm
根据《混规》式(6.2.14),M=Ne′=fyAs(h-as-as′)可得
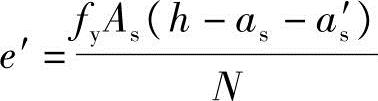
代入已知条件可得
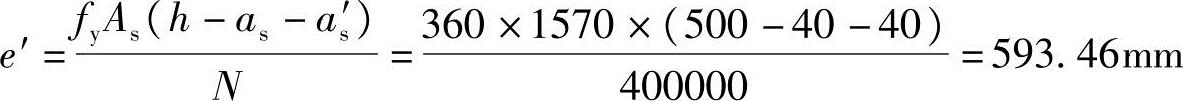
(5)求初始偏心距ei
根据《混规》图6.2.17,e′=ei-h/2+as′得
ei=e′+h/2-as′
得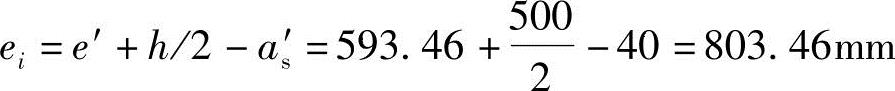
(6)求轴向压力对截面中心的偏心距e0
根据《混规》式(6.2.17-4),ei=e0+ea可得e0=ei-ea;
根据《混规》第6.2.5条,取e0=max(20mm,h/30):
h/30=500/30=16.7mm<20mm ea=20mm
e0=ei-ea=803.46-20=783.46mm
(7)求M
根据《混规》第6.2.17条,e0=M/N可得M=Ne0
M=Ne0=400×103×783.46=313.38kN·m
【例3.3.21】 偏心柱的承载力计算,已知N求M(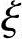 b≥
b≥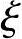 ≥2as′/h0)
≥2as′/h0)
条件:已知一钢筋混凝土偏心受压柱,截面尺寸为b×h=400mm×500mm,柱子的计算长度为l0=4.0m,混凝土强度等级为C30,纵向钢筋采用HRB400,对称配置纵向钢筋为5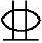 20,As=As′=1570mm2。柱上作用轴向力设计值为750kN,安全等级二级,环境类别一类。
20,As=As′=1570mm2。柱上作用轴向力设计值为750kN,安全等级二级,环境类别一类。
提示:本题所讨论的柱为短柱,不考虑长细比影响。
要求:求该柱能承受的弯矩设计值M。
解答:查《混规》表8.2.1知该柱的保护层厚度c=20mm,取as=as′=40mm,h0=h-as=500-40=460mm。
查《混规》表4.1.4,得fc=14.3N/mm2,ft=1.43N/mm2;
查《混规》表4.2.3-1,得fy=fy′=360N/mm2;
查《混规》第6.2.6条,得α1=1.0;
按《混规》式(6.2.7)计算,得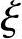 b=0.518。
b=0.518。
(1)验算每一侧纵向钢筋的最小配筋率
根据《混规》表8.5.1,ρ=As/bh≥0.2%
ρ=As/bh=1570/400×500=0.785%>ρmin=0.2%,通过。
验算全部纵向钢筋的最小配筋率:
根据《混规》表8.5.1,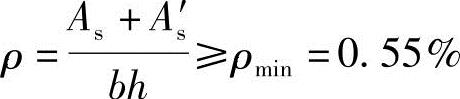
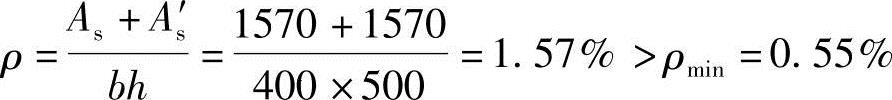
验算全部纵向钢筋的最大配筋率
根据《混规》第9.3.1条第1款,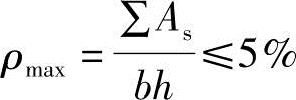
ρ=1.57%≤ρmax=5%,通过。
(2)求混凝土的压区高度x
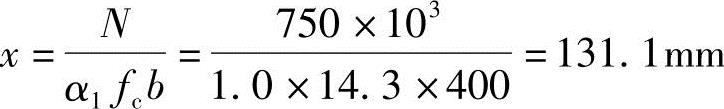
根据《混规》式(6.2.10-3)、式(6.2.10-4)得
x≤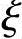 bh0; x≥2as′
bh0; x≥2as′
x=131.1mm<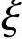 bh0=0.518×460=238.3mm>2as′=2×40=80mm
bh0=0.518×460=238.3mm>2as′=2×40=80mm
(3)求轴向力作用点到纵向钢筋合力点的距离e(或e′)
因为x满足《混规》式(6.2.10-3)、式(6.2.10-4)的要求,根据《混规》式(6.2.17-2)得
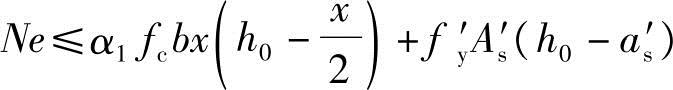
可得 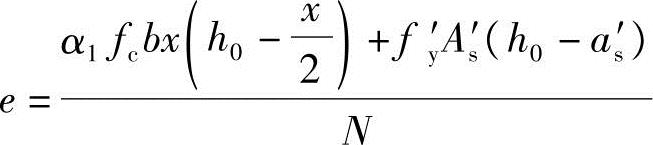
代入已知条件得
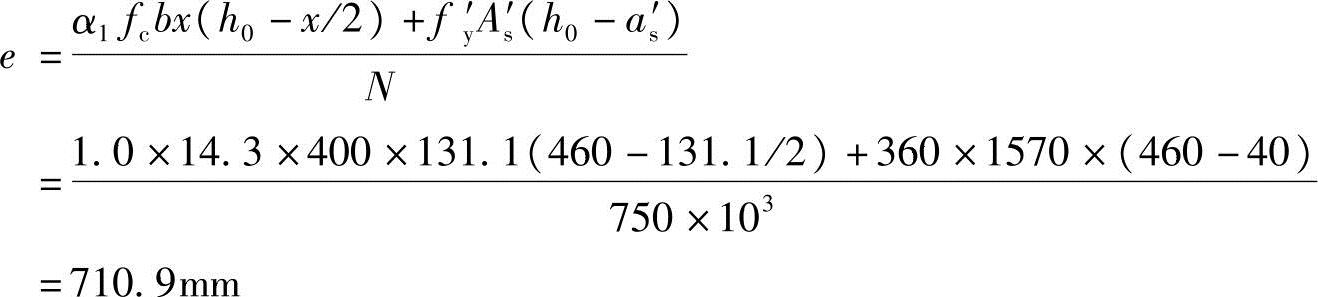
(4)求初始偏心距ei
根据《混规》式(6.2.17-3)e=ei+h/2-as,得到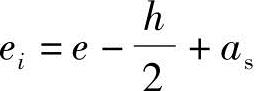
ei=e-h/2+as=710.9-500/2+40=500.9mm
(5)求轴向力对截面重心偏心距e0
根据《混规》式(6.2.17-4)ei=e0+ea得e0=ei-ea,根据《混规》第6.2.5条,取ea=(20mm,h/30)两者中的较大值:
h/30=500/30=16.7mm<20mm ea=20mm
e0=ei-ea=500.9-20=480.9mm
(6)求M
根据《混规》第6.2.17条,e0=M/N,M=Ne0,可得
M=Ne0=750×103×480.9=360.7kN·m
2)已知e0,求N
基本资料:已知截面尺寸b、h,纵向钢筋截面面积As=As′,材料强度fc、ft、fy;轴向压力对截面重心的偏心距e0;确定需用的计算参数α1、β1、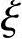 b、as、as′、h0。
b、as、as′、h0。
计算步骤:
①验算配筋率
a.验算每一侧纵向钢筋的最小配筋率
根据《混凝土结构设计规范》表8.5.1,当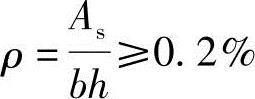 时通过,否则本题不成立。
时通过,否则本题不成立。
b.验算全部纵向钢筋的最小配筋率
根据《混凝土结构设计规范》表8.5.1,当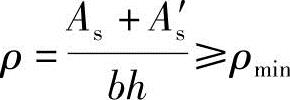 时通过,否则本题不成立。
时通过,否则本题不成立。
当钢筋强度等级为500MPa时,ρmin=0.50%
当钢筋强度等级为400MPa时,ρmin=0.55%
当钢筋强度等级为300MPa、335MPa时,ρmin=0.60%
c.验算全部纵向钢筋的最大配筋率
根据《混凝土结构设计规范》第9.3.1条第1款,当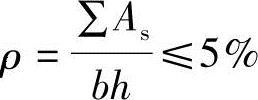 时通过,否则本题不成立。
时通过,否则本题不成立。
②求初始偏心距
根据《混凝土结构设计规范》式(6.2.17-4),ei=e0+ea;
根据《混凝土结构设计规范》第6.2.5条,取ea=(20mm,1/30h)二者中的较大值。
③求轴向力到纵向受拉钢筋合力点的距离e
根据《混凝土结构设计规范》式(6.2.17-3)得
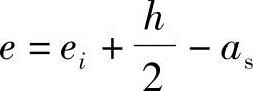
④求混凝土受压区高度x
应用《混凝土结构设计规范》式(6.2.17-1)、式(6.2.17-2)得
N=α1fcbx
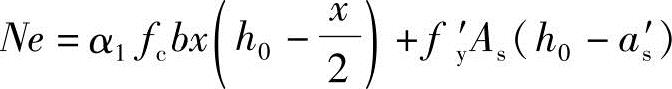
解联立方程求得x值。并验算x是否满足式(6.2.10-3)、式(6.2.10-4)。
⑤求轴向压力N
当x≥2as′时,解上述联立方程所求得的N值即为所求的N值;
当x<2as′时,根据《混凝土结构设计规范》式(6.2.14)得
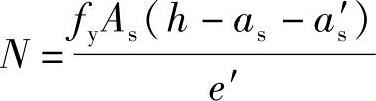
根据《混凝土结构设计规范》第6.2.17条第2款
此处 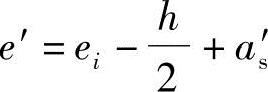
【例3.3.22】 偏压柱的承载力计算,已知e0求N(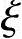 <2as′/h0)
<2as′/h0)
条件:已知矩形截面柱尺寸为b×h=500mm×700mm,混凝土强度等级C35,采用HRB400钢筋,对称配筋选用4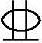 25,As=As′=1964mm2,构件计算长度l0=12m,安全等级二级,环境类别为一类。轴向力的偏心距e0=1000mm。
25,As=As′=1964mm2,构件计算长度l0=12m,安全等级二级,环境类别为一类。轴向力的偏心距e0=1000mm。
提示:本题所讨论的柱为短柱,不考虑长细比的影响。
要求:确定截面能承受的轴向力设计值N。
解答:(1)查《混规》表8.2.1知,环境类别为一类的柱的混凝土保护层厚度c=20mm,设as′=as=40mm,h0=h-as=700-40=660mm。
(2)查《混规》表4.1.4,得fc=16.7N/mm2;
查《混规》表4.2.3-1,得fy=fy′=360N/mm2;
查《混规》第6.2.6条,得α1=1.0;
按《混规》式(6.2.7-1),计算得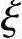 b=0.518。
b=0.518。
(3)验算配筋率
①验算一侧纵向钢筋的最小配筋率
根据《混规》表8.5.1,ρ=As/bh≥ρmin=0.2%
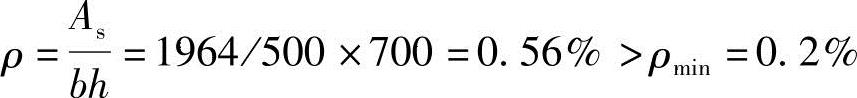
②验算全部纵向钢筋的最小配筋率
根据《混规》表8.5.1,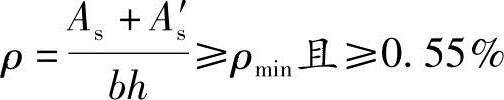
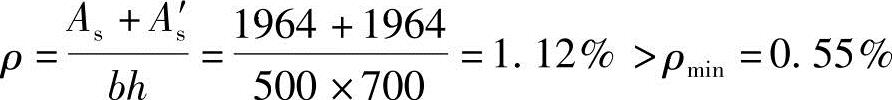
③验算全部纵向钢筋的最大配筋率
根据《混规》第9.3.1条第1款,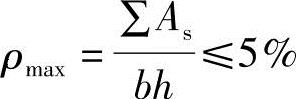
ρ=1.12%≤ρmax=5%
(4)求初始偏心距ei
根据《混规》式(6.2.17-4),ei=e0+ea;
根据《混规》第6.2.5条,取ea=max(20mm,h/30)
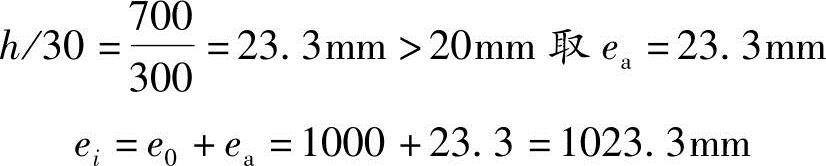
(5)求轴向力到纵向受拉钢筋合力点的距离e
根据《混规》式(6.2.17-3),e=ei+h/2-as可得
e=ei+h/2-as=1023.3+700/2-40=1333.3mm
(6)求混凝土压区高度x
应用《混规》式(6.2.17-1)、式(6.2.17-2),N=α1fcbx得
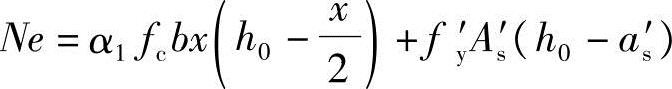
解联立方程
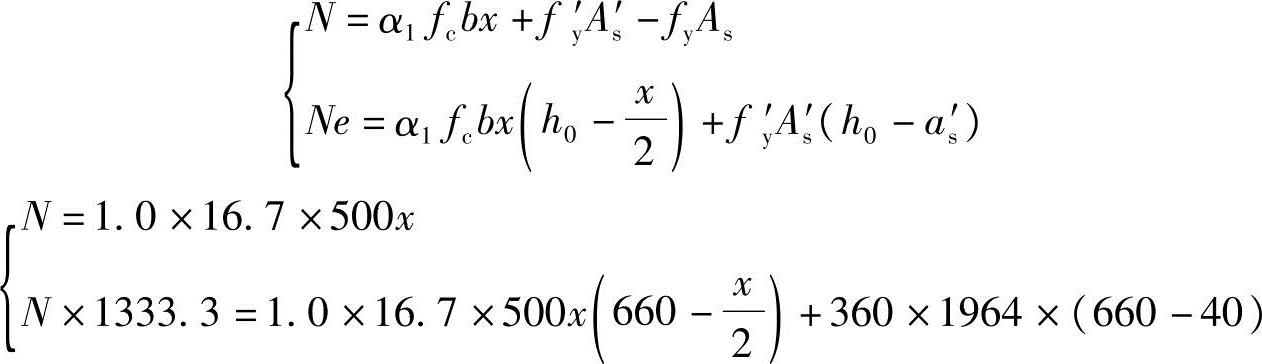
得x=73.8mm
(7)求轴向压力N
由于x=73.8mm<2as′=2×40=80mm
根据《混规》式(6.2.14),N=fyAs(h-as-as′)可得
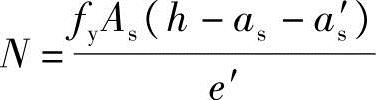
根据《混规》第6.2.17条第2款:
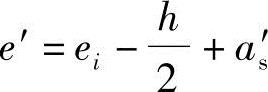
代入已知条件
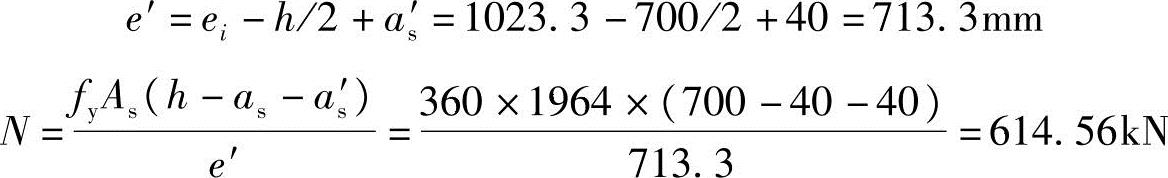
【例3.3.23】 偏压柱的承载力计算,已知e0求N(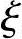 b≥
b≥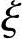 ≥2as′/h0)
≥2as′/h0)
条件:除轴向力偏心距e0=400mm外,其他条件和【例3.3.22】完全相同。
要求:确定截面能承受的轴向力设计值N。
解答:因为条件同【例3.3.22】,所以(1)验算配筋率同上例,略去。
(2)求初始偏心距ei
根据《混规》式(6.2.17-4),ei=e0+ea;
根据《混规》第6.2.5条,取ea=max(20mm,h/30)
h/30=700/30=23.3mm取ea=23.3mm
ei=e0+ea=400+23.3=423.3mm
(3)求轴向力到纵向受拉钢筋合力点的距离e
根据《混规》式(6.2.17-3),e=ei+h/2-as可得
e=ei+h/2-as=423.3+700/2-40=733.3mm
(4)求混凝土受压区高度x
应用《混规》式(6.2.17-1)、式(6.2.17-2)得
N=α1fcbx
Ne=α1fcbx(h0-x/2)+fy′As′(h0-as′)
可得联立方程
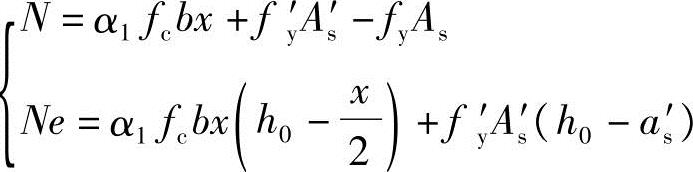
代入已知条件并由fy=fy′,As′=As得
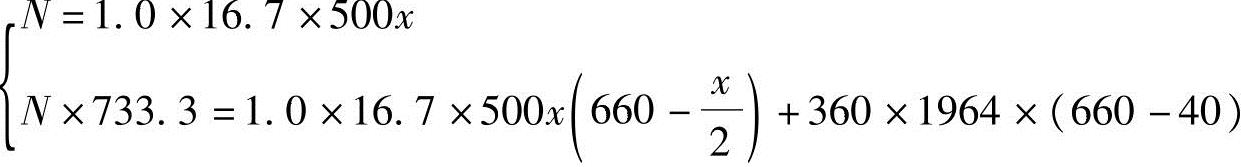
解得x=259mm。
(5)求轴向压力N
<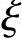 bh0=0.518×660=342mm
bh0=0.518×660=342mm
由于x=259mm
>2as′=2×40=80mm
将x=259mm代入《混规》式(6.2.17-1),得
N=α1fcbx=1.0×16.7×500×259=2161986N≈2162kN
4.模拟考题
(1)配筋计算
【3.3.16】 已知矩形截面柱尺寸b×h=400mm×500mm,承受轴力设计值N=1250kN,弯矩设计值M=285kN·m,采用C40混凝土,纵向钢筋为HRB400级钢,as=as′=35mm,采用对称配筋。则纵向受力钢筋As=As′(mm2)应为下列何项数值?
提示:本题所讨论的柱为短柱,不考虑长细比的影响。
(A)400 (B)600 (C)657 (D)700
答案:(C)
Ⅰ.详细解答
基本资料:根据《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条查得fc=19.1N/mm2,
fy=fy′=360N/mm2,α1=1.0,h0=h-as=500-35=465mm,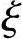 b=0.518
b=0.518
(1)确定初始偏心距ei
根据《混规》第6.2.17条的规定
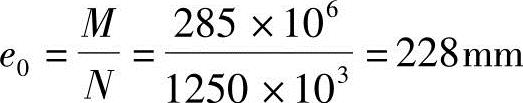
根据《混规》第6.2.5条:
ea=max{h/30,20}=20mm
其中,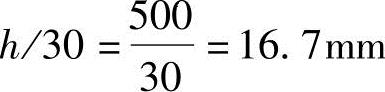
由《混规》式(6.2.17-3)得
ei=228+20=248mm
(2)求轴向力到纵向钢筋作用点的距离e(或e′)
由《混规》式(6.2.17-3)得
e=ei+h/2-as=248+250-35=463mm
(3)求混凝土压区高度
由《混规》式(6.2.17-1)得 ,为大偏心受压且x>2as′=2×35=70mm。
,为大偏心受压且x>2as′=2×35=70mm。
(4)求纵向钢筋As=As′
根据《混规》式(6.2.17-2)得
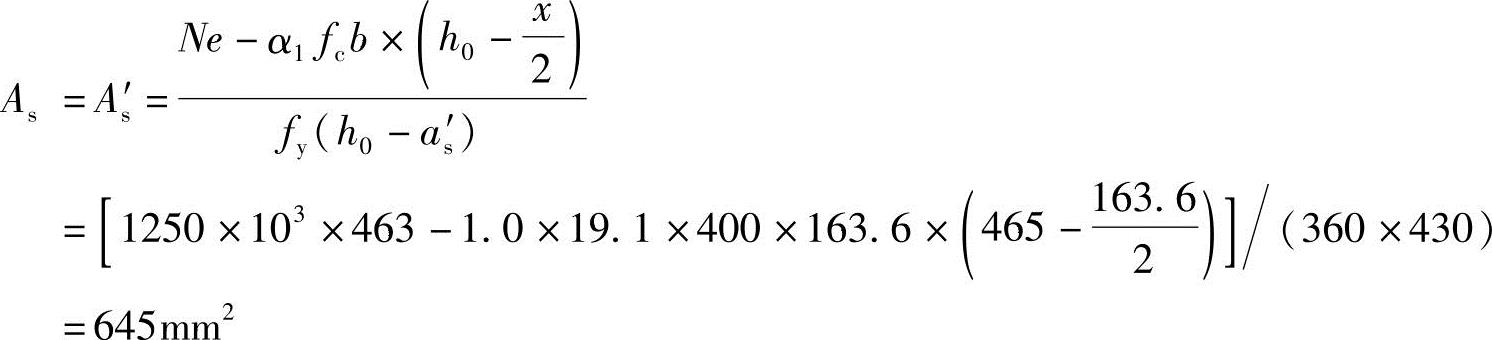
(5)验算每一侧纵向钢筋的最小配筋率
根据《混规》第8.5.1条的规定得
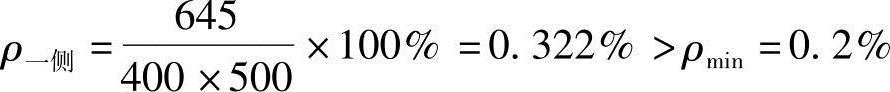
(6)验算全部纵向钢筋的最小配筋率
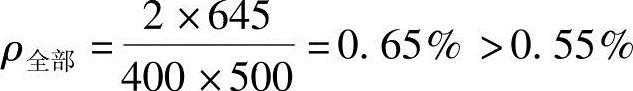
(7)验算全部纵向钢筋的最大配筋率
根据《混规》第9.3.1条第1款:
ρ=0.65%<ρmax=5%
Ⅱ.简要解答
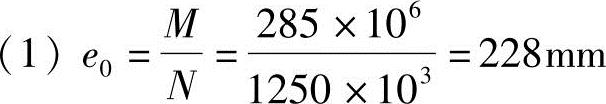
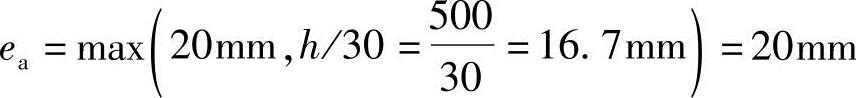
ei=e0+ea=228+20=248mm
(2)e=ei+h/2-as=248+500/2-35=463mm;

【3.3.17】 某偏心受压柱截面尺寸b×h=300mm×500mm,对称配筋,as=a′s=45mm,C30混凝土,HRB400级钢筋,计算长度l0=3500mm,承受轴向压力设计值N=1500kN,e0=100mm。As=As′(mm2)应为下列何项数值?
提示:本题所讨论的柱为短柱,不考虑长细比的影响。
(A)588 (B)750 (C)850 (D)950
答案:(A)
Ⅰ.详细解答
根据《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条查得:fc=14.3N/mm2,α1=1.0,β1=0.8,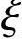 b=0.518,fy=360N/mm2=fy′,h0=h-as=500-45=455mm。
b=0.518,fy=360N/mm2=fy′,h0=h-as=500-45=455mm。
(1)确定初始偏心距ei
根据《混规》第6.2.5条,ea=500/30=16.7mm<20mm取ea=20mm
ei=e0+ea=100+20=120mm
(2)求轴向力到纵向钢筋作用点的距离e(或e′)
根据《混规》式(6.2.17-3)得
e=ei+h/2-as′=120+250-45=325mm
(3)求混凝土受压区高度x,并验算x
由《混规》式(6.2.17-1)、式(6.2.17-3)和式(6.2.17-4)

由于x>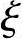 bh0
bh0
由《混规》式(6.2.17)的要求得
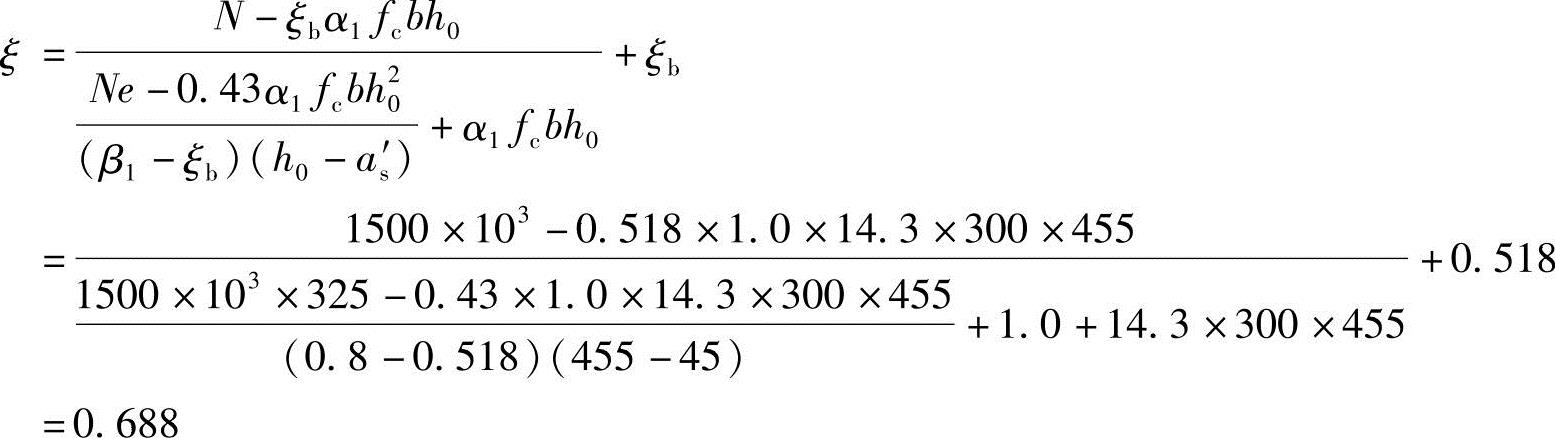
(4)求纵向钢筋As=As′
由《混规》式(6.2.17-2)得
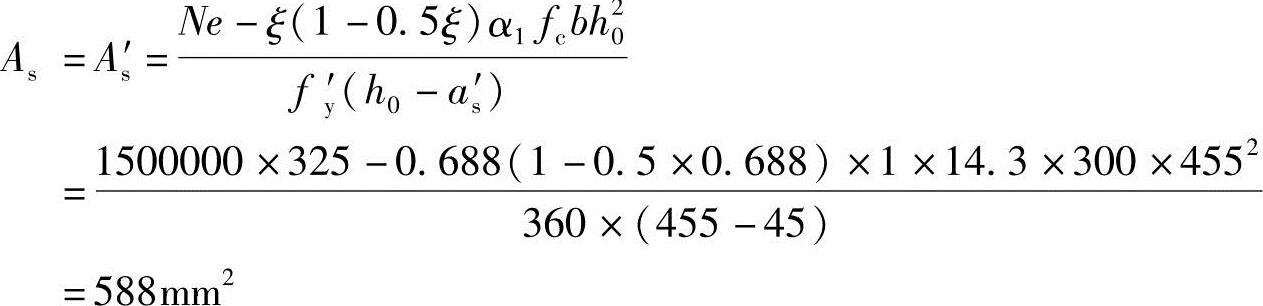
(5)验算每一侧纵向钢筋的最小配筋率
由《混规》表8.5.1得
单排ρ=588/(300×500)×100%=0.39%>ρmin=0.2%
(6)验算全部纵向钢筋的最小配筋率
由《混规》表8.5.1得
全部ρ=2×0.39%=0.78%>ρmin=0.55%,可以。
(7)验算全部纵向钢筋的最大配筋率
由《混规》第9.3.1条得
ρ=0.78%<ρmax=5%
Ⅱ.简要解答(https://www.xing528.com)

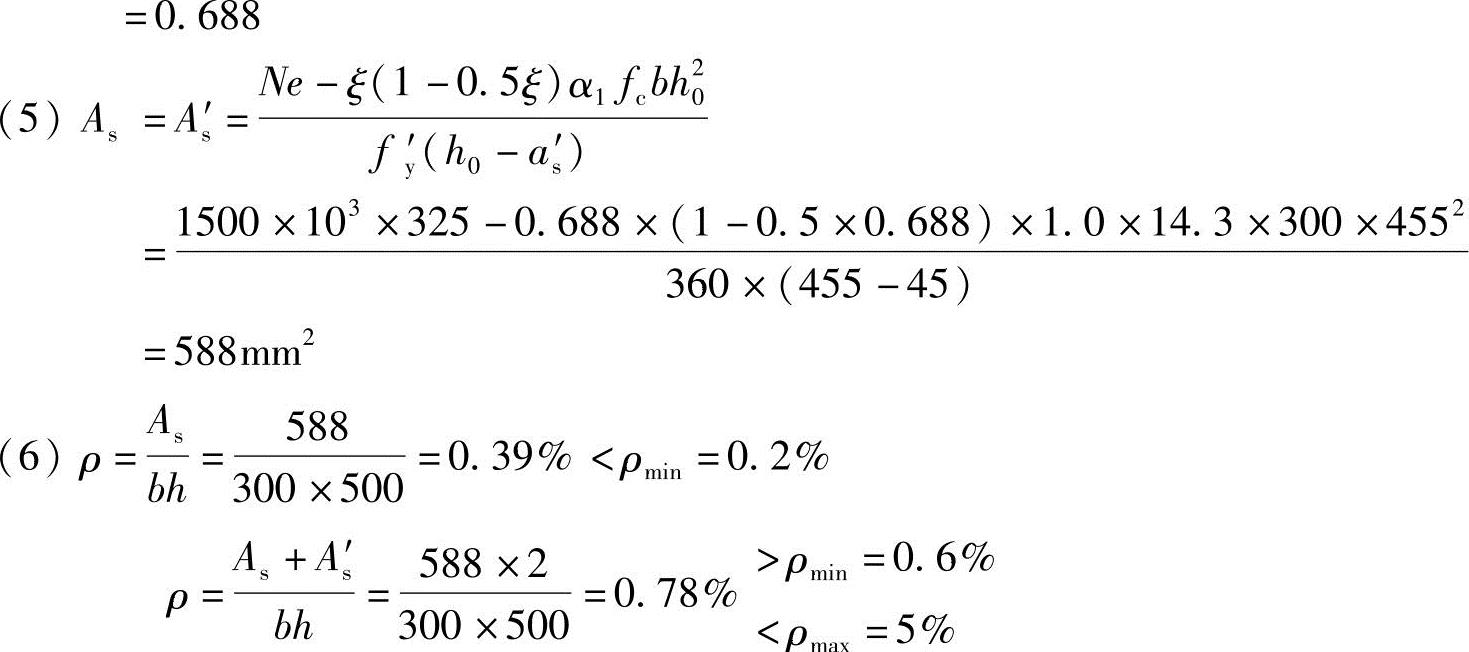
【3.3.18】~【3.3.19】 某钢筋混凝土柱的截面尺寸为300mm×500mm,柱计算长度l0=3m,轴向力设计值N=1300kN,弯矩设计值M=253kN·m。采用混凝土强度等级为C25,纵向受力钢筋采用HRB400级。
提示:本题所讨论的柱为短柱,不考虑长细比的影响。
【3.3.18】 若设计成对称配筋,相对受压区高度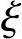 应为下列何项数值?
应为下列何项数值?
(A)0.981 (B)0.644 (C)0.55 (D)0.418
答案:(B)
Ⅰ.详细解答
根据《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条,查得fc=11.9N/mm2,α1=1.0,β1=0.8,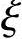 b=0.518。
b=0.518。
根据《混规》第8.2.1条,c=20mm;
取as=as′=40mm h0=h-as=500-40=460mm;
若设计成对称配筋,相对受压区高度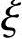 应为何项数值?
应为何项数值?
(1)确定初始偏心距ei
由《混规》式(6.2.17)得
e0=M/N=253×106/1300×103=194.6mm
根据《混规》第6.2.5条,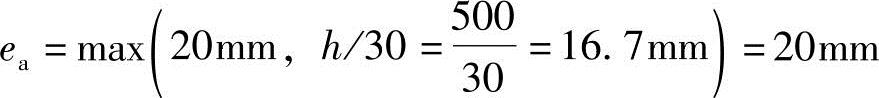
ei=e0+ea=194.6+20=214.6mm
(2)求轴向力到纵向钢筋作用点的距离e(或e′)
e=ei+h/2-as=214.6+500/2-40=424.6mm
(3)求混凝土压区高度x
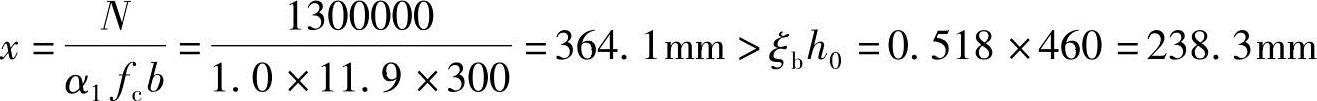
因为x≥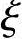 bh0所以要求
bh0所以要求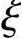 。
。
由《混规》式(6.2.17-8)得
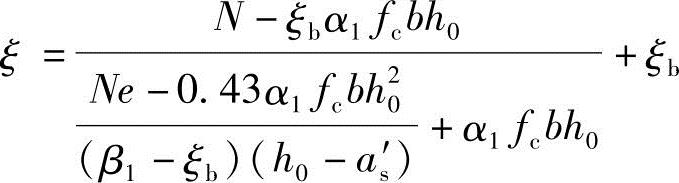
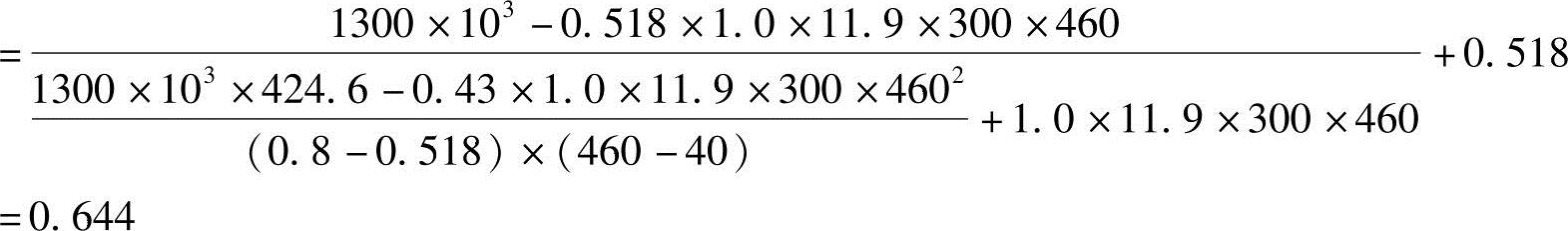
Ⅱ.简要解答

【3.3.19】 若已知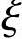 =0.829,对称配筋,则As和As′(mm2)应为下列何项数值?
=0.829,对称配筋,则As和As′(mm2)应为下列何项数值?
(A)2056 (B)1226 (C)1972 (D)2496
答案:(B)
由《混规》式(6.2.17-2)并取x=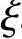 h0,可得
h0,可得
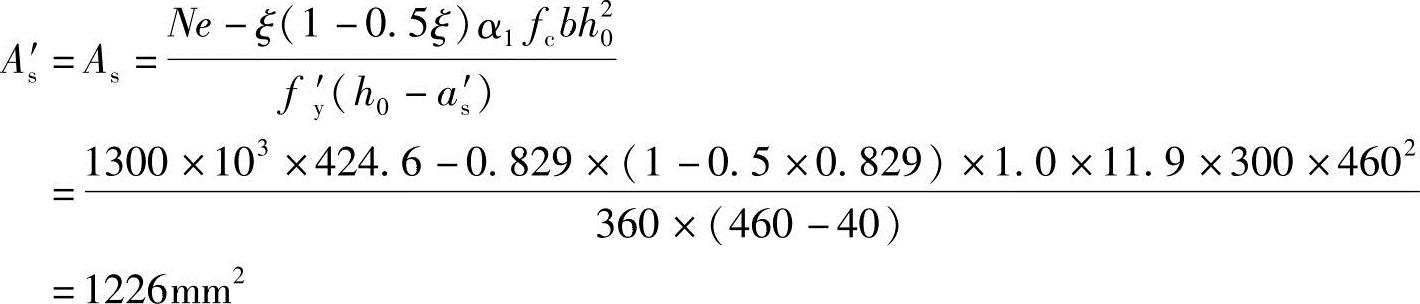
(2)承载力计算
【3.3.20】 已知一钢筋混凝土偏心受压柱截面尺寸为b×h=400mm×500mm,柱子的计算长度l0=4000mm。混凝土强度等级为C30,纵向钢筋HRB400,as=40mm。柱每侧配置5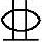 20的钢筋,As′=As=1570mm2,柱子上作用轴向力设计值N=400kN。且已知构件为大偏心受压。求该柱能承受的弯矩设计值M(kN·m)?
20的钢筋,As′=As=1570mm2,柱子上作用轴向力设计值N=400kN。且已知构件为大偏心受压。求该柱能承受的弯矩设计值M(kN·m)?
提示:本题所讨论的柱为短柱,不考虑长细比的影响。
(A)315 (B)267 (C)345 (D)392
答案:(A)
Ⅰ.详细解答
基本资料:根据《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条查得
fc=14.3N/mm2,fy=fy′=360N/mm2,α1=1.0,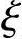 b=0.518,h0=h-as=500-40=460mm。
b=0.518,h0=h-as=500-40=460mm。
(1)验算配筋率
①验算每一侧纵向钢筋的最小配筋率
根据《混规》第8.5.1条得
ρ=As/bh=1570/(400×500)=0.785%≥ρmin=0.2%
②验算全部纵向钢筋的最小配筋率
根据《混规》第8.5.1条得
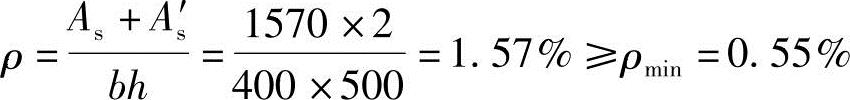
③验算全部纵向钢筋的最大配筋率
根据《混规》第9.3.1条第1款:
ρ=1.57%<ρmax=5%
(2)求混凝土压区高度x,并验算是否满足《混规》式(6.2.10-3)、式(6.2.10-4):

x≤2as′=2×40=80mm
(3)求轴向力作用点到纵向钢筋合力点的距离e(或e′)
因x≤2as′由《混规》式(6.2.14)求得
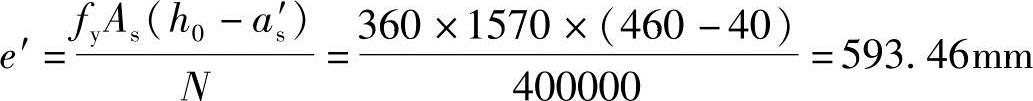
(4)求初始偏心距ei
根据《混规》图6.2.17得
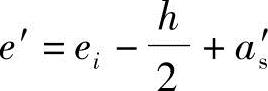
ei=e′+h/2-as′=593.46+500/2-40=803.46mm
(5)求轴向力对截面重心的偏心距e0
根据《混规》(6.2.17-4)和第6.2.5条:
初始偏心距ei=803.46mm,附加偏心距ea=max{20,h/30}=max{20,17}=20mm。轴向压力对截面重心的偏心距:e0=ei-ea=803.46-20=783.46mm
(6)求M
根据《混规》第6.2.17条得
M=Ne0=400×103×783.46=313.4kN·m
Ⅱ.简要解答
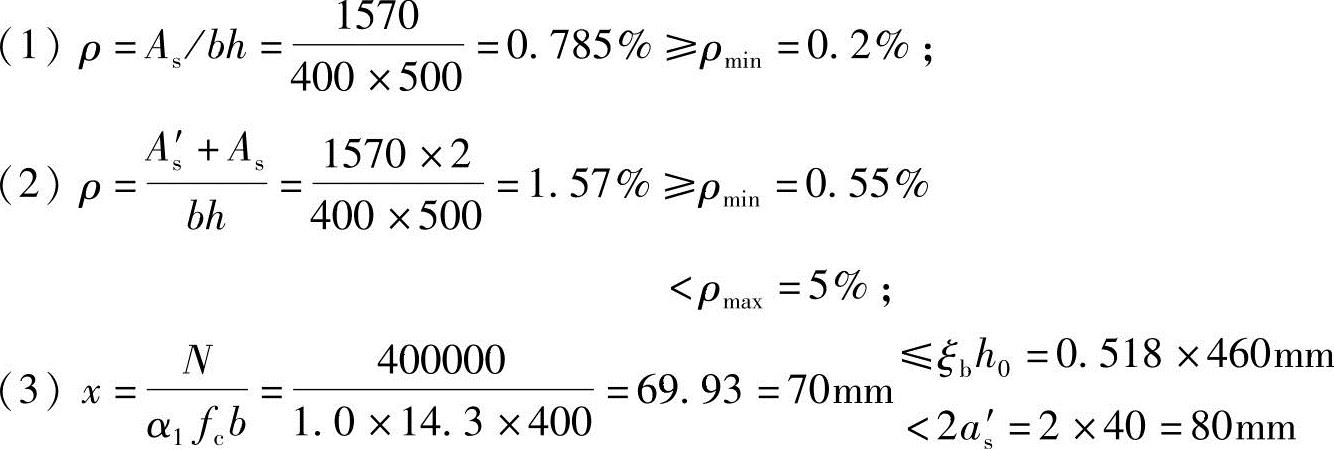
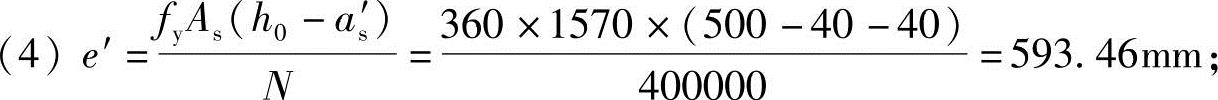
(5)ei=e′+h/2-as′=593.46+500/2-40=803.46mm;
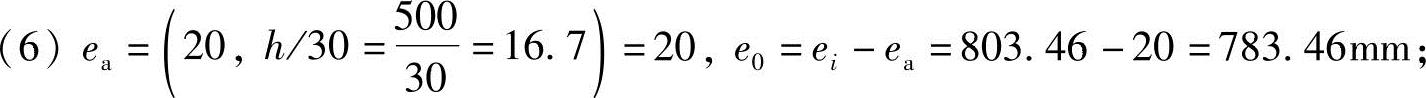
(7)M=Ne=400000×783.46=313.38kN·m
【3.3.21】 已知偏压构件b=400mm,h=500mm,采用C30级混凝土,HRB400级钢筋,该柱采用对称配筋,受拉和受压钢筋均为2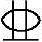 16+2
16+2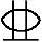 14,若给定偏心距e0=200mm,则该构件承受的内力设计值N(kN)、M(kN·m)应为下列何项数值?
14,若给定偏心距e0=200mm,则该构件承受的内力设计值N(kN)、M(kN·m)应为下列何项数值?
提示:本题为短柱,不考虑长细比的影响。
(A)1447.2,318.38 (B)1447.2,289.43
(C)1230.3,270.67 (D)1290,258.05
答案:(D)
Ⅰ.详细解答
基本资料:根据《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条、8.2.1条查得:
fc=14.3N/mm2,fy=f′y=360N/mm2,α1=1.0,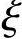 b=0.518,c=20mm,as=a′s=40mm,h0=460mm,As=1017mm2,e0=200mm。
b=0.518,c=20mm,as=a′s=40mm,h0=460mm,As=1017mm2,e0=200mm。
由《混规》附录A查得As=As′=710mm2。
(1)验算配筋率
①每一侧纵向钢筋的最小配筋率
根据《混规》第8.5.1条得
ρ=As/bh=710/400×500=0.355%≥ρmin=0.2%
②全部纵向钢筋的最小配筋率
根据《混规》第8.5.1条得
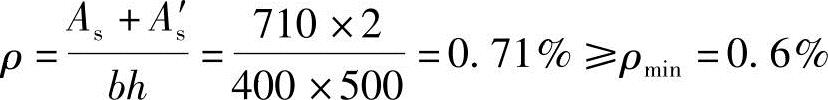
③全部纵向钢筋的最大配筋率
根据《混规》第9.3.1条第1款:
ρ=0.71%<ρmax=5%
(2)求ei
根据《混规》式(6.2.17-4)和式(6.2.5)得
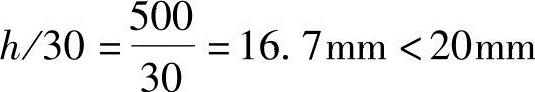 取ea=20mm
取ea=20mm
ei=e0+ea=200+20=220mm
(3)求轴向力到纵向钢筋作用点的距离e和e′
根据《混规》式(6.2.17-3)和图6.2.17得
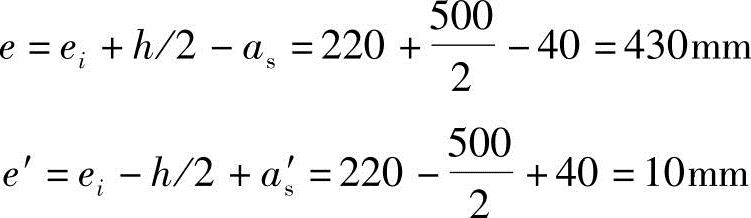
(4)求x(图3.3.39)
先假设N作用在截面以外,为大偏心,对轴向力N取矩(图3.3.37)得

代入已知条件,有
360×710×430=360×710×10+1.0×14.3×400x(220-500/2+0.5x)
x2-60x-37536=0
解得 x=226.1mm<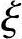 bh0
bh0
=0.518×460=238.3mm
假定大偏压成立
(5)求N和M
根据《混规》式(6.2.17-1)得
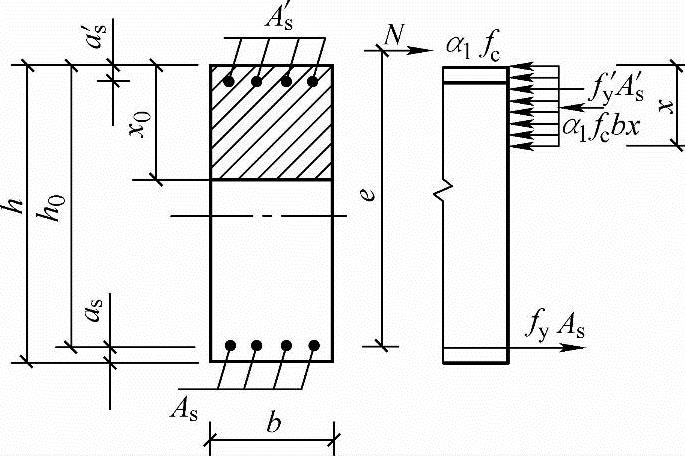
图 3.3.39
N=α1fcbx=1.0×14.3×400×226.1=1293kN
M=Ne0=1293×0.2=258.6kN·m
Ⅱ.简要解答
(1)ρ=As/bh=710/400×500=0.355%≥ρmin=0.2%;
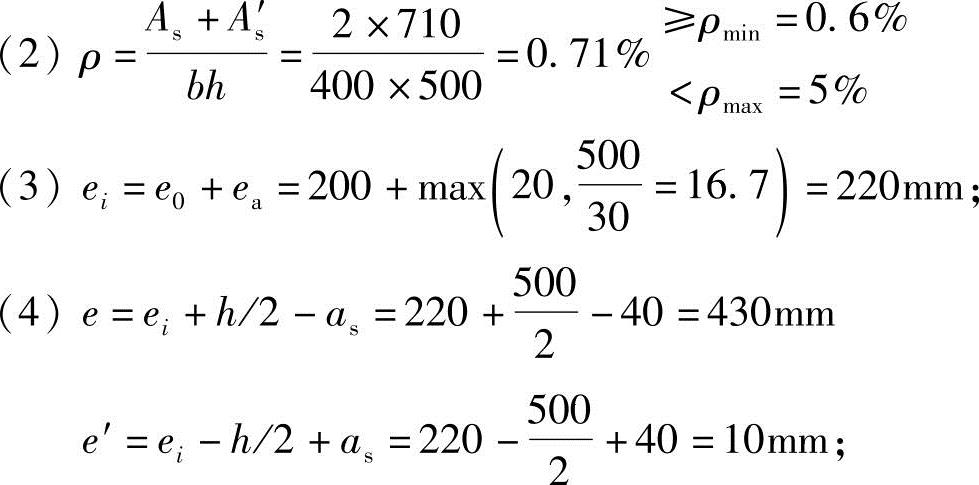
(5)假设N作用在截面以外为大偏压(图3.3.39),对N取矩得
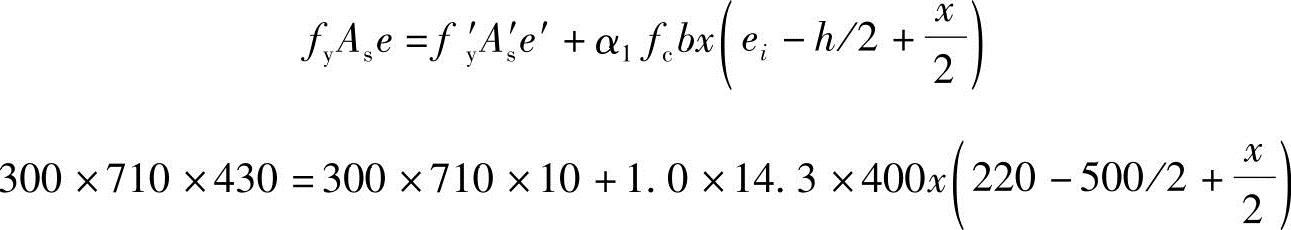
解得x=226.1mm<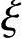 bh0=0.518×460=238.3mm
bh0=0.518×460=238.3mm
(6)N=α1fcbx=1.0×14.3×400×226.1=1293kN
M=Ne0=1293×0.2=258.6kN·m
(四)考虑“二阶效应”的弯矩设计值
1.准备知识
(1)一阶弯矩和二阶弯矩
钢筋混凝土长柱在荷载作用下会产生横向挠度δ,图3.3.40所列出的长柱中间横向变形的实测情况清楚地表明了这一点。
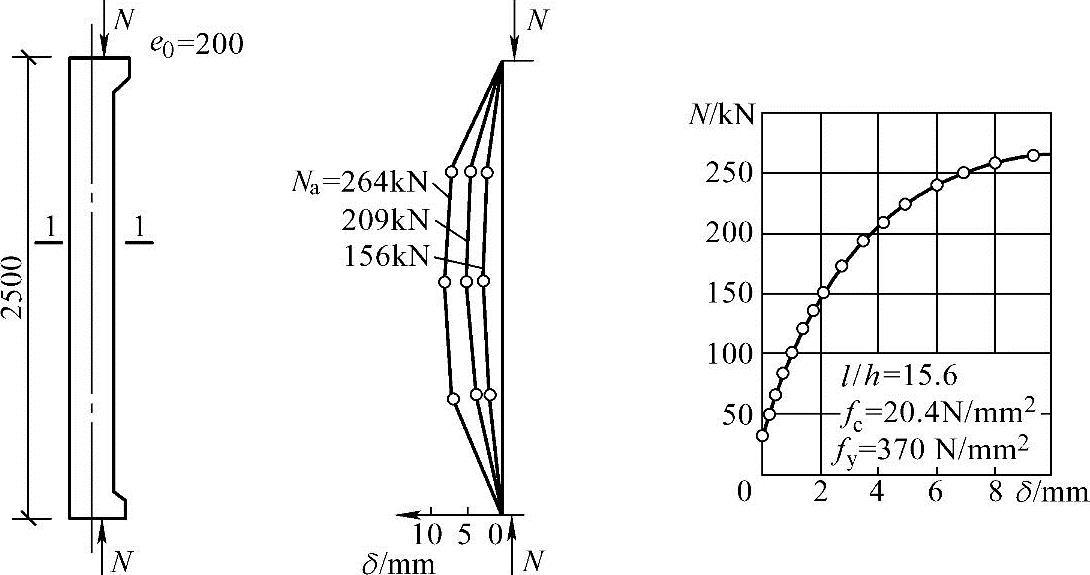
图3.3.40 钢筋混凝土长柱在荷载作用下的横向变形
混凝土长柱在荷载作用下产生横向挠度δ,提高了柱的横向总侧移量ei+δ,故构件承担的实际弯矩M=N(ei+δ),其值明显大于初始弯矩M0=Nei,这种由加载后构件的变形而引起的内力增大的情况,称为“二阶效应”。初始弯矩称为“一阶弯矩”,附加弯矩称为“二阶弯矩”,图3.3.41列出了这种情况。
当框架结构上作用水平荷载,或虽无水平荷载,但结构或荷载不对称,或二者均不对称时,结构会产生侧移Δ,如图3.3.38所示。这时竖向荷载在产生了侧移Δ的框架中亦会引起附加内力,这类附加内力亦为“二阶弯矩”。
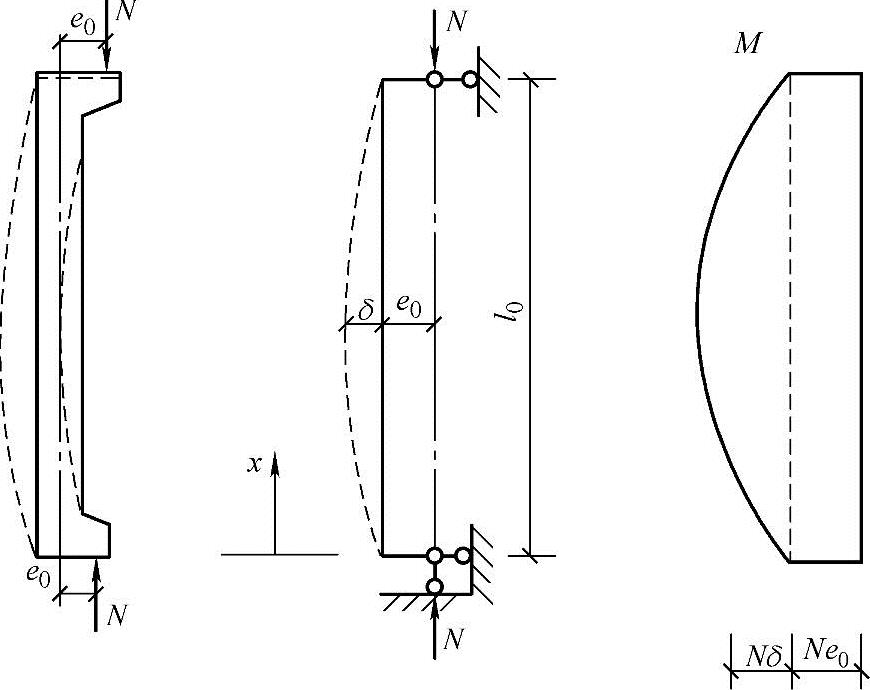
图3.3.41 P-δ效应
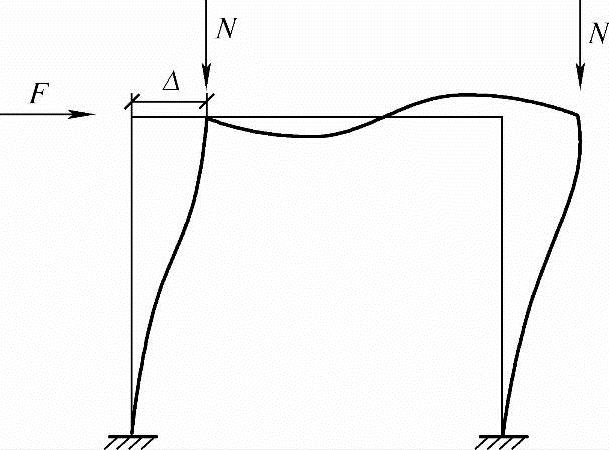
图3.3.42 P-Δ效应
上面所说的二阶弯矩,亦称二阶效应。结构工程中的二阶效应泛指在产生了挠曲变形或层间位移的结构构件中,由轴向压力所引起的附加内力。如对无侧移的框架结构,二阶效应是指轴向压力在产生了挠曲变形δ的柱段中引起的附加内力,通常称为P-δ效应(图3.3.41),它可能增大柱段中部的弯矩,一般不增大柱端控制截面的弯矩。对于有侧移的框架结构,二阶效应主要是指竖向荷载在产生了侧移Δ的框架中引起的附加内力,通常称为P-Δ效应(图3.3.42)。
在结构分析中求得的是构件两端截面的弯矩及轴力,考虑二阶效应后,在构件的某个其他截面,其弯矩可能会大于端部截面的弯矩。设计时应取弯矩最大的截面进行计算。
(2)结构无侧移时偏心受压构件的二阶弯矩
结构无侧移时,根据偏心受压构件两端弯矩值的不同,纵向弯曲引起的二阶弯矩可能遇到以下三种情况。
1)构件两端弯矩值相等且单曲率弯曲
图3.3.43a表示构件两端作用着由一阶分析求得的偏心距为ei的轴向压力N,故两端的弯矩均为Nei。在Nei作用下,构件将产生如图虚线所示的弯曲变形,其中δ表示在最大弯矩点由弯曲引起的侧移;这时柱高中间的总弯矩值Mmax为
Mmax=Nei+Nδ
式中 Nδ——由纵向弯曲引起的附加弯矩(图3.3.43b)。
2)构件两端弯矩值不相等且单曲率弯曲
构件承受的两端弯矩不相等,但两端弯矩均使构件的同一侧受拉(单曲率弯曲)时,其最大侧移出现在离端部的某一距离处,如图3.3.44a所示,其中M2=Nei2、M1=Nei1,M2>M1。考虑附加偏心距δ后,图3.3.44d所示的最大弯矩Mmax=Md+Nδ,式中Nδ为纵向弯曲引起的附加弯矩,如图3.3.44c所示。
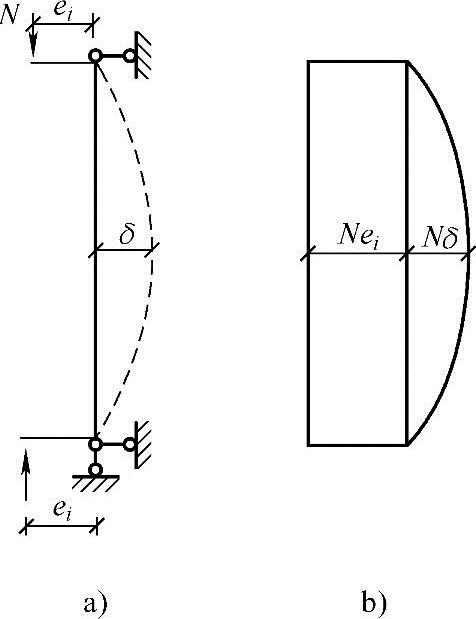
图3.3.43 两端弯矩值相等时的二阶弯矩
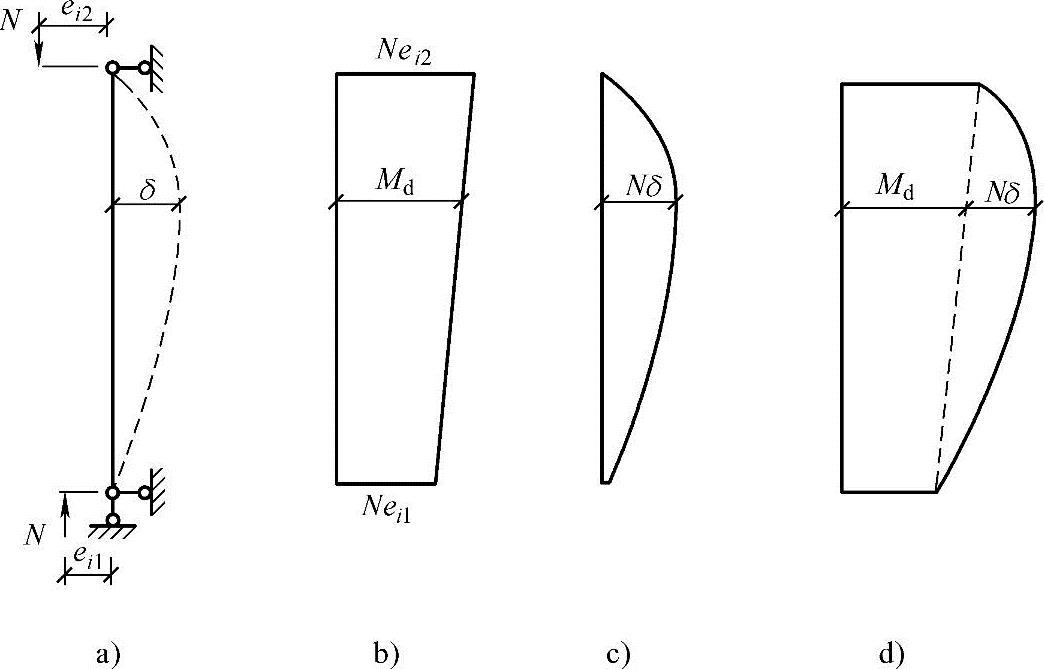
图3.3.44 两端弯矩值相等时的二阶弯矩
3)构件两端弯矩值不相等且双曲率弯曲
图3.3.45a表示构件两端弯矩值不相等且双曲率弯曲的情况。由两端不相等弯矩M2=Nei2、M1=Nei1引起的构件弯矩分布如图3.3.45b所示;纵向弯曲引起的二阶弯矩Nδ,如图3.3.45c所示;总弯矩M=Md+Nδ有两种可能的分布,如图3.3.45d、e所示。图3.3.45d中,二阶弯矩未引起最大弯矩的增加,即构件的最大弯矩在柱端,并等于Nei2。图3.3.45e中,最大弯矩在距柱端某一距离处,其值Mmax=Md+Nδ。
根据上述分析,可得以下几点结论:
①当一阶弯矩最大处与二阶弯矩最大处相重合时(图3.3.43),弯矩增加得最多,即临界截面上的弯矩最大。
②当两个端弯矩值不相等但单曲率弯曲时(图3.3.44),弯矩仍将增加较多。
③当构件两端弯矩值不相等且双曲率弯曲时(图3.3.45),沿构件产生一个反弯点,弯矩增加很少,考虑二阶效应后的最大弯矩值一般不会超过构件端部弯矩或稍有增大。
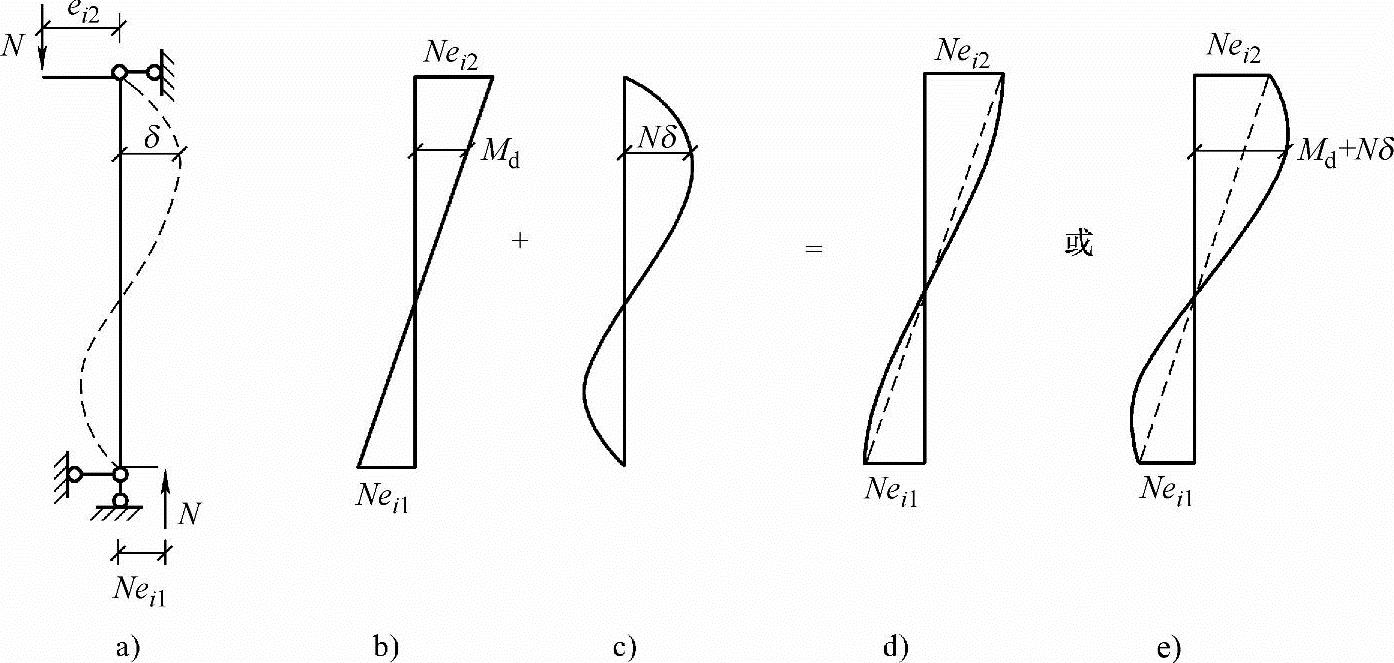
图3.3.45 两端弯矩值不相等且符号相反时的二阶弯矩
(3)结构有侧移时偏心受压构件的二阶弯矩
考虑图3.3.46所示的简单门架,承受水平荷载F和竖向力N的作用。仅由水平力F引起的变形在图3.3.46a中用虚线表示,弯矩MF如图3.3.46b所示。当N作用时,产生了附加弯矩和附加变形,变形用实线表示,附加弯矩用图3.3.46c的弯矩图表示,此时二阶弯矩为结构侧移和杆件变形所产生的附加弯矩的总和。由图3.3.46b、c可见,最大的一阶弯矩和二阶弯矩均出现在柱端且同号,临界截面上的弯矩为一阶弯矩与二阶弯矩之和,如图3.3.46d、e所示。
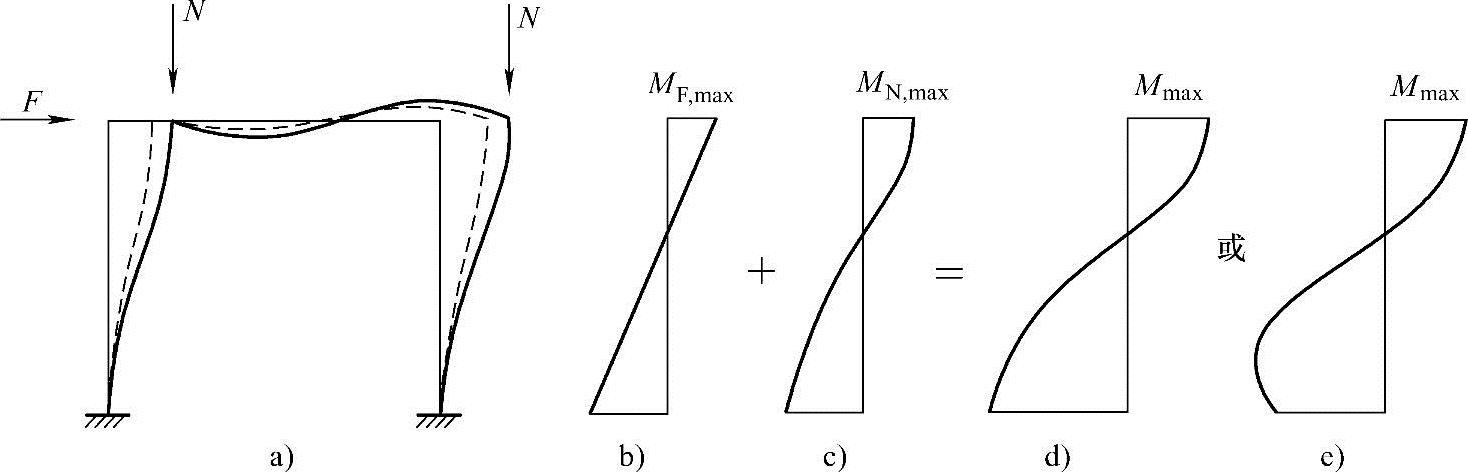
图3.3.46 结构侧移引起的二阶弯矩
a)计算简图 b)F引起的弯矩 c)N引起的弯矩 d)、e)F+N引起的弯矩
2.考试要求
(1)《考试大纲》的要求:掌握
(2)“试题”回顾
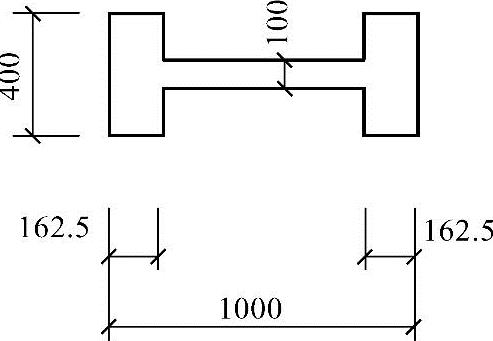
图 3.3.47
【试题3.3.18】 工形截面柱偏心矩增大系数(2001年)
假定厂房柱采用C30级混凝土,主筋为Ⅱ级钢筋,下柱为工形截面,其截面尺寸如图3.3.47所示;截面的有效高度h0=960mm,构件的截面面积A=1.975×103mm2;截面内力为M=563.75kN·m,N=696.48kN;对称配筋,系大偏心受压构件。试通过计算并指出其偏心矩增大系数η与下列何项数值最为接近?
(A)1.061 (B)1.138 (C)1.61 (D)1.066
【试题3.3.19】 偏心距增大系数(2002年)
有一承受非恒载为主的钢筋混凝土框架柱,安全等级Ⅱ级,矩形截面尺寸为b×h=300mm×500mm,对称配筋,每侧各配有3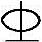 22钢筋(As=942mm2),
22钢筋(As=942mm2),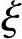 b=0.544,混凝土强度等级为C25,纵向受拉钢筋合力点至截面近边距离as=40mm,该柱的计算长度l0=4.5m。该柱在某荷载效应组合状态下,初始偏心距ei=150mm。试问该柱在该组荷载作用下的偏心距增大系数η与下列何项数值最为接近?
b=0.544,混凝土强度等级为C25,纵向受拉钢筋合力点至截面近边距离as=40mm,该柱的计算长度l0=4.5m。该柱在某荷载效应组合状态下,初始偏心距ei=150mm。试问该柱在该组荷载作用下的偏心距增大系数η与下列何项数值最为接近?
提示: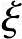 1可按给出的近似公式进行计算:
1可按给出的近似公式进行计算: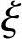 1=0.2+2.7ei/h0。
1=0.2+2.7ei/h0。
(A)1.181 (B)1.205 (C)1.177 (D)1.207
【试题3.3.20】 排架上柱考虑二阶弯矩影响的偏心矩增大系数(2006年)
某一设有吊车的单层厂房柱(屋盖为刚性屋盖),上柱长Hu=3.5m,截面尺寸为400mm×400mm,下柱长Hl=10.0m,截面尺寸为400mm×900mm,上、下柱均对称配筋,as=as′=40mm。混凝土强度等级为C25,纵向受力钢筋采用HRB335级热轧钢筋。当考虑横向水平地震作用组合时,在排架方向内力组合的最不利设计值为:上柱M=100kN·m,N=200kN;下柱M=700kN·m,N=1200kN。该柱上柱的截面曲率修正系数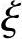 1=1.0,构件长细比对截面曲率的影响系数
1=1.0,构件长细比对截面曲率的影响系数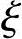 2=0.97,
2=0.97,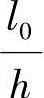
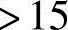 ,
,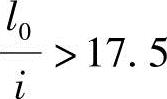 ,
,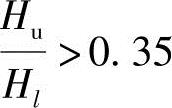 。试问,上柱在排架方向考虑二阶弯矩影响的轴向压力偏心距增大系数η,与下列何项数值最为接近?
。试问,上柱在排架方向考虑二阶弯矩影响的轴向压力偏心距增大系数η,与下列何项数值最为接近?
(A)1.15 (B)1.36 (C)1.66 (D)1.86
【试题3.3.21】 框架底层中柱的偏心距增大系数(2008年)
某钢筋混凝土框架结构多层办公楼,安全等级为二级,框架抗震等级为二级。该房屋各层层高均为3.6m,首层地面标高为±0.00m,基础顶面标高为-1.00m,框架柱截面尺寸为b×h=500mm×500mm,混凝土强度等级为C30,柱纵向钢筋采用HRB335级钢筋(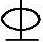 ),柱箍筋采用HPB235级钢筋(
),柱箍筋采用HPB235级钢筋(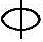 ),as=as′=45mm。
),as=as′=45mm。
已知该框架底层中柱调整后的轴向压力设计值对截面重心的偏心距e0=195mm,截面曲率修正系数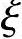 1=0.7,构件长细比对截面曲率的影响系数
1=0.7,构件长细比对截面曲率的影响系数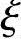 2=1.0,截面尺寸为b×h=500mm×500mm。试问,当采用装配式楼盖时,该框架柱偏心距增大系数与以下何项数值最为接近?
2=1.0,截面尺寸为b×h=500mm×500mm。试问,当采用装配式楼盖时,该框架柱偏心距增大系数与以下何项数值最为接近?
提示:该框架柱水平荷载产生的弯矩设计值小于总弯矩设计值的75%。
(A)1.09 (B)1.14 (C)1.15 (D)1.20
【试题3.3.22】 排架柱偏心距增大系数(2009年)
某钢筋混凝土单层单跨厂房(有吊车,屋面为刚性屋盖),其排架柱的上柱Hu=3.3m,下柱Hl=11.5m,上、下柱截面尺寸如图3.3.48所示。当考虑横向水平地震作用组合时,在排架方向内力组合的最不利设计值为:上柱M=110kN·m,N=250kN;下柱M=580kN·m,N=730kN。混凝土强度等级为C30,纵向受力钢筋采用HRB335级钢筋(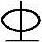 );对称配筋,as=as′=40mm。
);对称配筋,as=as′=40mm。
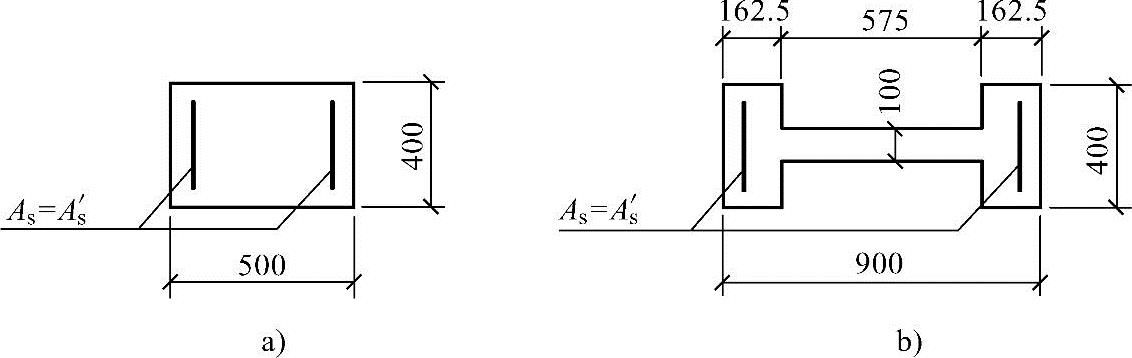
图 3.3.48
a)上柱截面 b)下柱截面
假设上柱在排架方向的计算长度l0=8.0m,截面曲率修正系数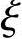 1=1.0。试问,该上柱在排架方向的偏心距增大系数η,应与下列何项数值最为接近?
1=1.0。试问,该上柱在排架方向的偏心距增大系数η,应与下列何项数值最为接近?
(A)1.12 (B)1.15 (C)1.18 (D)1.21
3.不考虑“二阶弯矩”的范围
《混凝土结构设计规范》规定:
6.2.3 弯矩作用平面内截面对称的偏心受压构件,当同一主轴方向的杆端弯矩比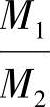 不大于0.9且轴压比不大于0.9时,若构件的长细比满足式(6.2.3)的要求,可不考虑轴向压力在该方向挠曲杆件中产生的附加弯矩影响;否则应根据本规范第6.2.4条的规定,按截面的两个主轴方向分别考虑轴向压力在挠曲杆件中产生的附加弯矩影响。
不大于0.9且轴压比不大于0.9时,若构件的长细比满足式(6.2.3)的要求,可不考虑轴向压力在该方向挠曲杆件中产生的附加弯矩影响;否则应根据本规范第6.2.4条的规定,按截面的两个主轴方向分别考虑轴向压力在挠曲杆件中产生的附加弯矩影响。
lc/i≤34-12(M1/M2) (6.2.3)
式中 M1、M2——已考虑侧移影响的偏心受压构件两端截面按结构弹性分析确定的对同一主轴的组合弯矩设计值,绝对值较大端为M2,绝对值较小端为M1,当构件按单曲率弯曲时,M1/M2取正值,否则取负值;
lc——构件的计算长度,可近似取偏心受压构件相应主轴方向上下支撑点之间的距离;
i——偏心方向的截面回转半径。
偏心受压长柱的二阶弯矩对于计算内力时已考虑侧移影响和无侧移的结构的偏心受压构件,若杆件的长细比较大时,在轴向压力作用下,应考虑由于杆件自身挠曲对截面弯矩产生的不利影响,即通常所谓的P-δ效应。P-δ效应一般会增大杆件中间区段截面的弯矩,特别是当杆件较细长,杆件两端弯矩同号(即均使杆件同侧受拉)且两端弯矩的比值接近1.0时,可能出现杆件中间区段截面的一阶弯矩考虑P-δ效应后的弯矩值超过杆端弯矩的情况。从而,使杆件中间区段截面成为设计的控制截面。
相反,在结构中常见的反弯点位于柱高中部的偏心受压构件,二阶效应虽能增大构件除两端区域外各截面的曲率和弯矩,但增大后的弯矩通常不可能超过柱两端控制截面的弯矩。因此,在这种情况下,P-δ效应不会对杆件截面的偏心受压承载力产生不利影响。
《混凝土结构设计规范》给出了可不考虑P-δ效应的条件。《混凝土结构设计规范》规定,弯矩作用平面内截面对称的偏心受压构件,当同一主轴方向的杆端弯矩比不大于0.9,且轴压比小于0.90,若杆件长细比满足《混凝土结构设计规范》式(6.2.3)条件,可不考虑轴向压力在该方向挠曲杆件中产生的附加弯矩的影响。否则,应按两个主轴方向分别考虑轴向压力在挠曲杆件中产生的附加弯矩影响。
具体计算时可按下列步骤进行。
基本资料:已知截面尺寸b、h,弯矩作用平面内柱计算长度l0,材料强度fc;外部荷载效应M、N。
计算步骤:
(1)验算杆端弯矩比
当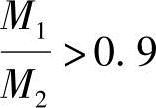 时,需考虑二阶效应。
时,需考虑二阶效应。
当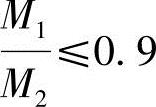 时,转入(2)。
时,转入(2)。
(2)验算轴压比
当f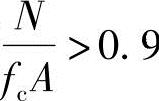 时,需考虑二阶效应。
时,需考虑二阶效应。
当f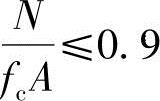 时,转入(3)。
时,转入(3)。
(3)验算长细比
当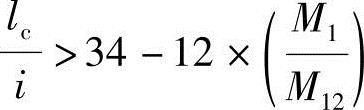 时,需考虑二阶效应。
时,需考虑二阶效应。
当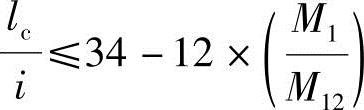 时,不需考虑二阶效应。
时,不需考虑二阶效应。
式中 i——截面回转半径。
【例3.3.24】 判断是否需考虑二阶效应
条件:钢筋混凝土框架柱,截面尺寸为b=400mm、h=700mm,构件计算长度l0=2.5m,柱轴向力设计值N=2400kN,柱端弯矩设计值Ml=M2=240kN·m,混凝土C30(fc=14.3N/mm2)。
要求:判断是否需考虑二阶效应。
解答:验算杆端弯矩比
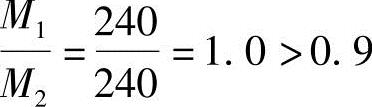
根据《混规》第6.2.3条的规定:“当同一主轴方向的杆端弯矩比M1/M2不大于0.9可不考虑轴向压力在该方向挠曲杆件中产生的附加弯矩影响”;本题的杆端弯矩比M1/M2=1.0>0.9,不符合上述M1/M2≤0.9的规定,故需考虑二阶弯矩的影响。
【例3.3.25】 判断是否需要考虑轴向力在弯曲方向的二阶效应
条件:某钢筋混凝土偏心受压柱的截面尺寸为b×h=400mm×700mm,弯矩作用平面内的计算长度为5.4m,混凝土强度等级C25(fc=11.9N/mm2),承受的弯矩设计值M1=200kN·m,M2=240kN·m,与M2对应的轴向力设计值为N=3800kN。
要求:判断是否需要考虑轴向力在弯曲方向的二阶效应。
解答:
(1)验算柱两端弯矩的比值
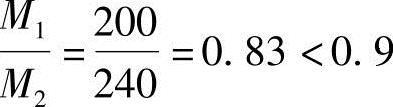
(2)验算柱的轴压比
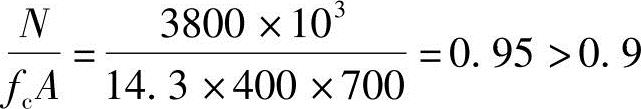
根据《混规》第6.2.3条的规定,应考虑杆件自身挠曲变形的影响。
【例3.3.26】 判断构件是否需要考虑附加弯矩
条件:柱截面尺寸b=400mm,h=400mm,截面承受轴向压力设计值N=350kN,柱顶截面弯矩设计值M1=90kN·m,柱底截面弯矩设计值M2=105kN·m。柱挠曲变形为单曲率。弯矩作用平面内柱上下两端的支撑长度为9.6m,混凝土强度等级为C35,fc=16.7N/mm2。
要求:判断构件是否需要考虑附加弯矩。
解答:基本资料:b=400mm,h=400mm,lc=9.6m,fc=16.7N/mm2;M1=90kN·m,M2=105kN·m,N=350kN。
(1)验算杆端弯矩比
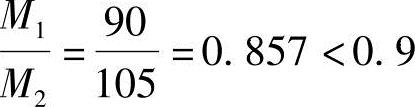
(2)验算轴压比
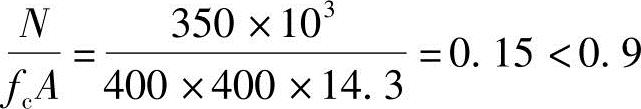
(3)验算长细比
截面回转半径 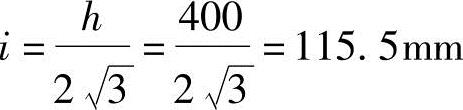 长细比
长细比 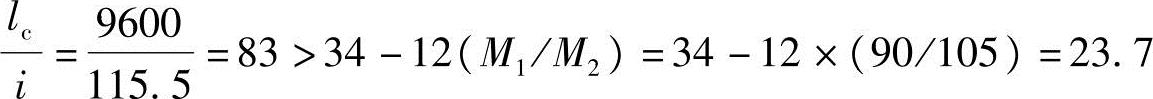
根据《混规》第6.2.3条的规定,应考虑杆件自身挠曲变形的影响。
【例3.3.27】 判断是否需考虑二阶效应
条件:钢筋混凝土框架柱,截面尺寸为b×h=400mm×450mm。柱的计算长度l0=4000mm,承受轴向压力设计值N=320kN,柱端弯矩设计值M1=-100kN·m,M2=300kN·m。混凝土强度等级为C30(fc=14.3N/mm2)。
要求:判断是否需考虑二阶效应。
解答:基本资料:b=400mm,h=450mm,lc=4.0m,fc=14.3N/mm2;M1=-100kN·m,M2=300kN·m,N=320kN。
(1)验算杆端弯矩比
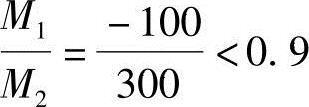
(2)验算轴压比
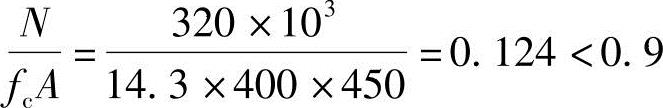
(3)验算长细比
A=b×h=400×450=180000mm2
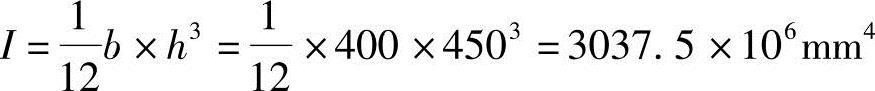
截面回转半径 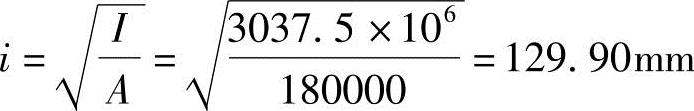
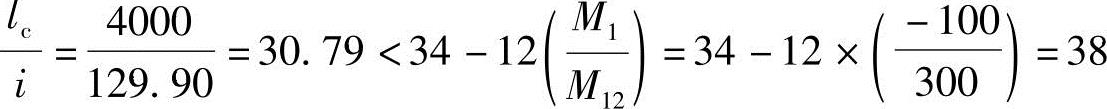
根据《混规》第6.2.3条的规定,可不考虑二阶效应的影响。
4.非排架结构柱考虑二阶效应的弯矩设计值
《混凝土结构设计规范》规定:
6.2.4 除排架结构柱外,其他偏心受压构件考虑轴向压力在挠曲杆件中产生的二阶效应后控制截面的弯矩设计值,应按下列公式计算:
M=CmηnsM2 (6.2.4-1)
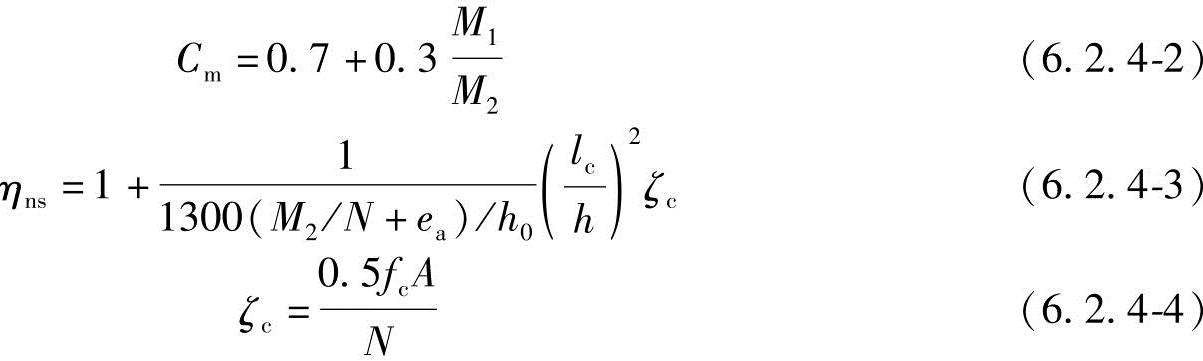
当Cmηns小于1.0时取1.0;对剪力墙及核心筒墙,可取Cmηns等于1.0。
式中 Cm——构件端截面偏心距调节系数,当小于0.7时取0.7;
ηns——弯矩增大系数;
N——与弯矩设计值M2相应的轴向压力设计值;
ea——附加偏心距,按本规范第6.2.5条确定;
ζc——截面曲率修正系数,当计算值大于1.0时取1.0;
h——截面高度;对环形截面,取外直径;对圆形截面,取直径;
h0——截面有效高度;对环形截面,取h0=r2+rs;对圆形截面,取h0=r+rs;此处,r、r2和rs,按本规范第E.0.3条和第E.0.4条确定;
A——构件截面面积。
(1)两端铰支等偏心距单向压弯构件
图3.3.49为一两端铰支的细长杆件,两端对称平面内作用初始偏心距为ei的轴向压力N。它在杆件两端产生的弯矩为同号弯矩。杆件在弯矩作用平面内将产生单曲率弯曲变形,设在中间截面的挠度为δ。该截面上的初始偏心距由ei增加至(ei+δ),则构件控制截面的弯矩为:
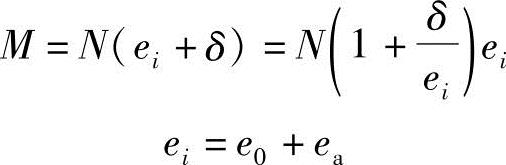
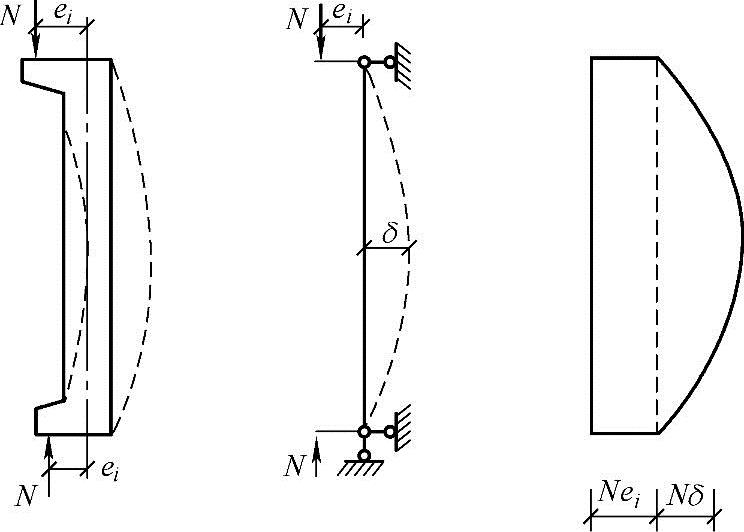
图3.3.49 铰支柱的弯矩和附加弯矩
令 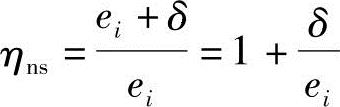
M=ηnsNei
式中 N——与弯矩设计值对应的轴向压力设计值;
ηns——弯矩增大系数。
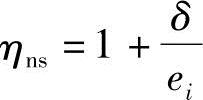
从上面铰支柱弯矩计算公式的推演过程可知,两端铰支等偏心距的细长柱考虑二阶弯矩后控制截面的弯矩等于一阶弯矩乘以弯矩增大系数。因此,若求构件控制截面弯矩就要求得弯矩增大系数ηns。
《混凝土结构设计规范》第6.2.4条式(6.2.4-3)给出了弯矩增大系数ηns的表达式。
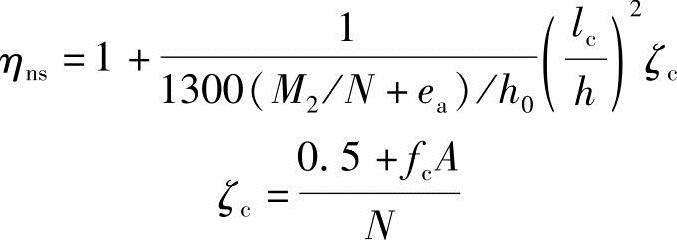
【例3.3.28】 计算控制截面的弯矩设计值
条件:钢筋混凝土框架柱,截面尺寸为b×h=400mm×450mm。柱的计算长度lc=5000mm,承受轴向压力设计值N=480kN,柱端弯矩设计值M1=M2=350kN·m,混凝土强度等级为C30(fc=14.3N/mm2)。
提示:需考虑二阶效应的影响。
要求:计算控制截面的弯矩设计值
解答:(1)按《混规》第6.2.5条得
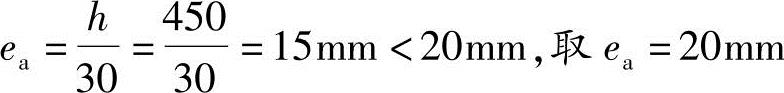
(2)按《混规》式(6.2.4-4)计算得
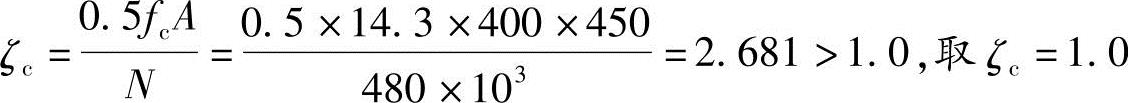
(3)按《混规》式(6.2.4-3)计算得
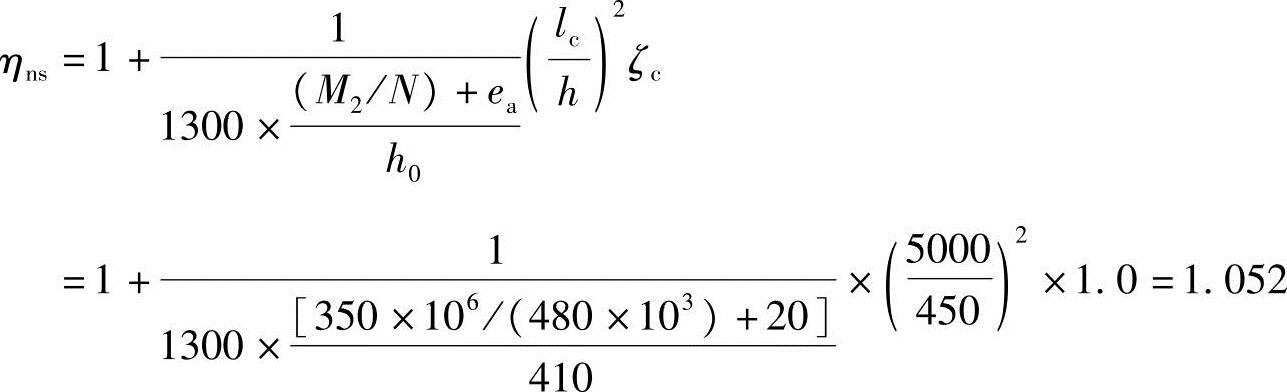
(4)按《混规》式(6.2.4-2)计算得
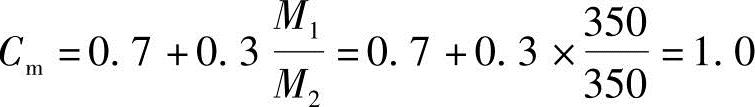
(5)按《混规》式(6.2.4-1)计算控制截面的弯矩设计值
M=ηnsCmM2=1.052×1.0×350=368.2kN·m
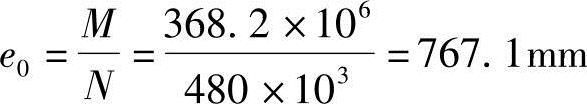
(2)两端铰支不等偏心距单向压弯构件
图3.3.50a表示两端铰支不等偏心距的单向压弯构件。设构件A端的弯矩为M1=Nei1;B端的弯矩为M2=Nei2,并设|M2|≥|M1|。在二阶弯矩的影响下,其总弯矩图如图3.3.50b所示,其控制截面的弯矩为M1max。
现用一等效柱来替代原柱。等效柱为两端铰支等偏心距Cmei2的压弯构件,等效柱两端的一阶弯矩为NCmei2,在二阶弯矩的影响下其总弯矩图如图3.3.50d所示,控制截面位于构件1/2高度处,其弯矩为MⅡmax。
两柱等效,即两柱的承载力相等,MⅠmax=MⅡmax=M。
等效柱法是指把求两端铰支不等偏心距(ei1,ei2)的压弯构件控制截面弯矩MⅠmax,变换成求与其等效的两端铰支等偏心距Cmei2的压弯构件控制截面的弯矩MⅡmax。其中,Cm称为构件端部截面偏心距调节系数,参见图3.3.50c。《混凝土设计规范》第6.2.4条式(6.2.4-2)给出了偏心受压构件端部截面偏心距调节系数的表达式。
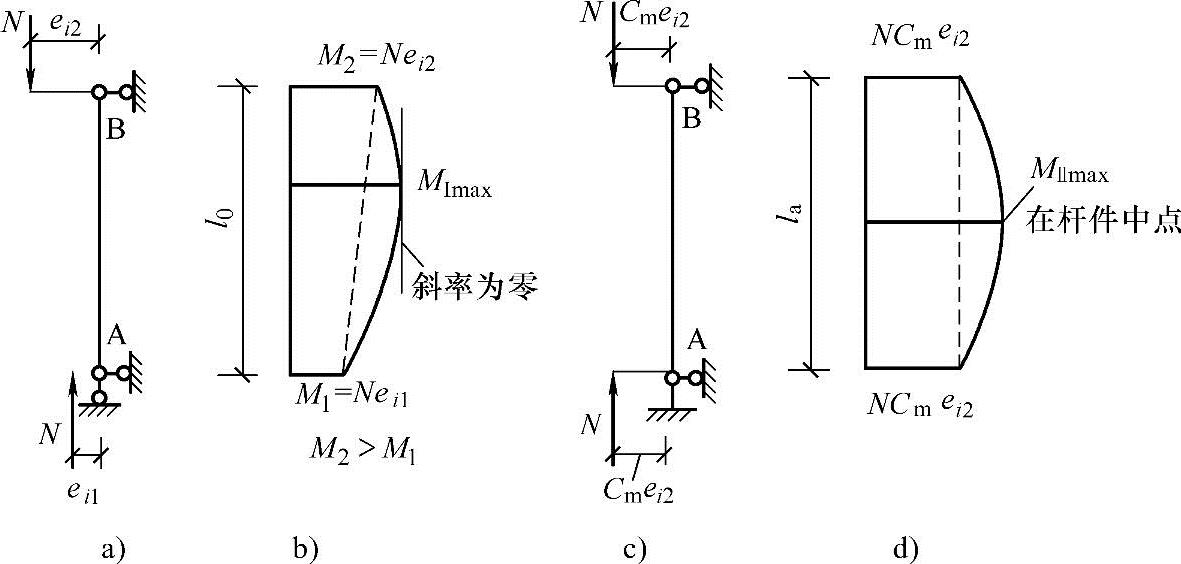
图3.3.50 两端铰支不等偏心距受压构件的计算
a)原柱 b)原柱弯矩图 c)等效柱 d)等效柱弯矩图
【例3.3.29】 计算控制截面的弯矩设计值
条件:已知偏心受压柱截面尺寸为b×h=400mm×600mm,轴向压力设计值N=2500kN。弯矩设计值M1=50kN·m,M2=80kN·m。柱的计算长度lc=6m。混凝土强度等级为C25,采用HRB400级钢筋,截面采用对称配筋。
提示:需考虑二阶效应的影响。
要求:计算控制截面的弯矩设计值。
解答:按《混规》第6.2.5条得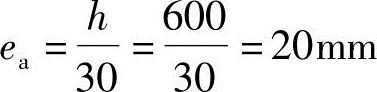 ,取ea=20mm
,取ea=20mm
按《混规》式(6.2.4-4)计算得
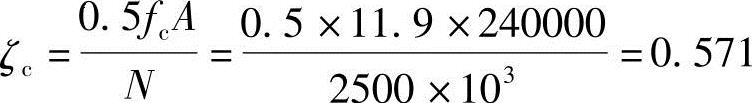
按《混规》式(6.2.4-3)计算得
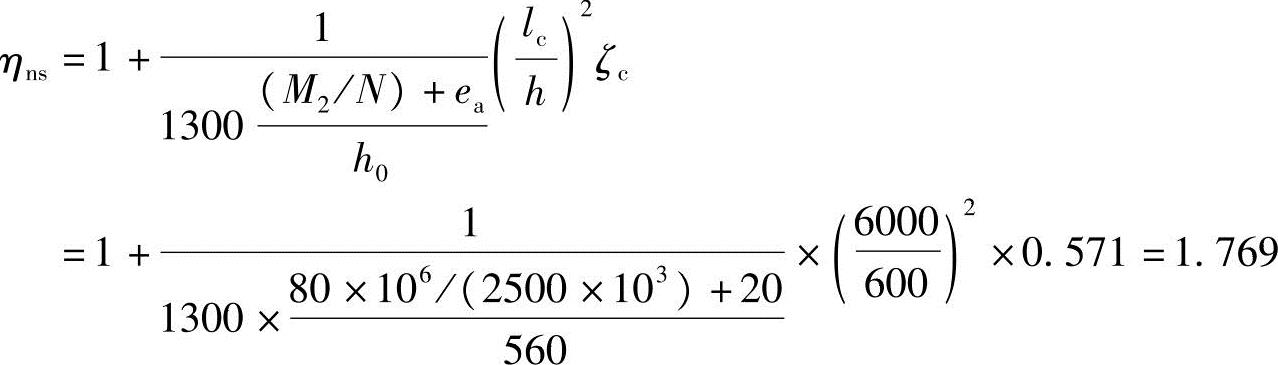
按《混规》式(6.2.4-2)计算得
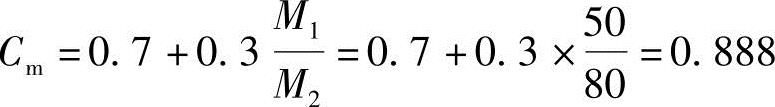
按《混规》式(6.2.4-1)计算控制截面的弯矩设计值
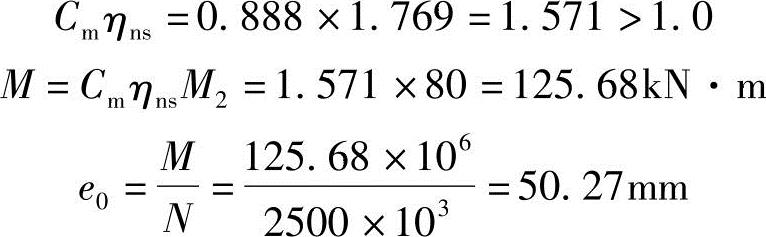
【例3.3.30】 框架底层中柱弯矩的Cmηns(2008年,因规范改版,本题已作相应调整。)
某钢筋混凝土框架结构多层办公楼,安全等级为二级,框架抗震等级为二级。该房屋各层层高均为3.6m,首层地面标高为±0.00m,基础顶面标高为-1.00m,框架柱截面尺寸为b×h=500mm×500mm,混凝土强度等级为C30,柱纵向钢筋采用HRB400级钢筋( ),柱箍筋采用HRB300级钢筋(
),柱箍筋采用HRB300级钢筋( ),as=as′=45mm。
),as=as′=45mm。
已知该框架底层中柱调整后的轴向压力设计值为N=2145kN,柱上下端弯矩为M上=167.31kN·m,M下=418.215kN·m,上下端弯矩使柱产生同向弯曲。试问,该柱的Cmηns与以下何项数值最为接近?
(A)1.00 (B)1.14 (C)1.15 (D)1.20
答案:(A)
(1)根据《混规》6.2.3条:
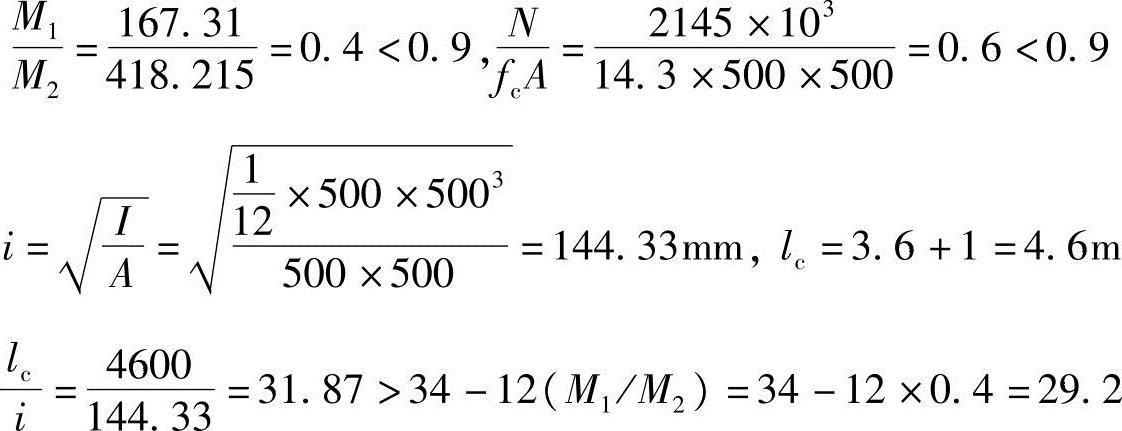
需考虑轴向压力在挠曲杆件中产生的附加弯矩影响。
(2)根据《混规》6.2.5条,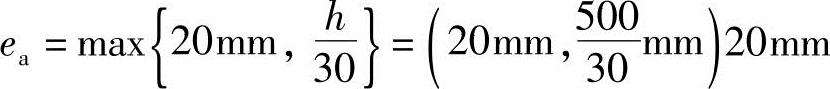
(3)根据《混规》6.2.4条:
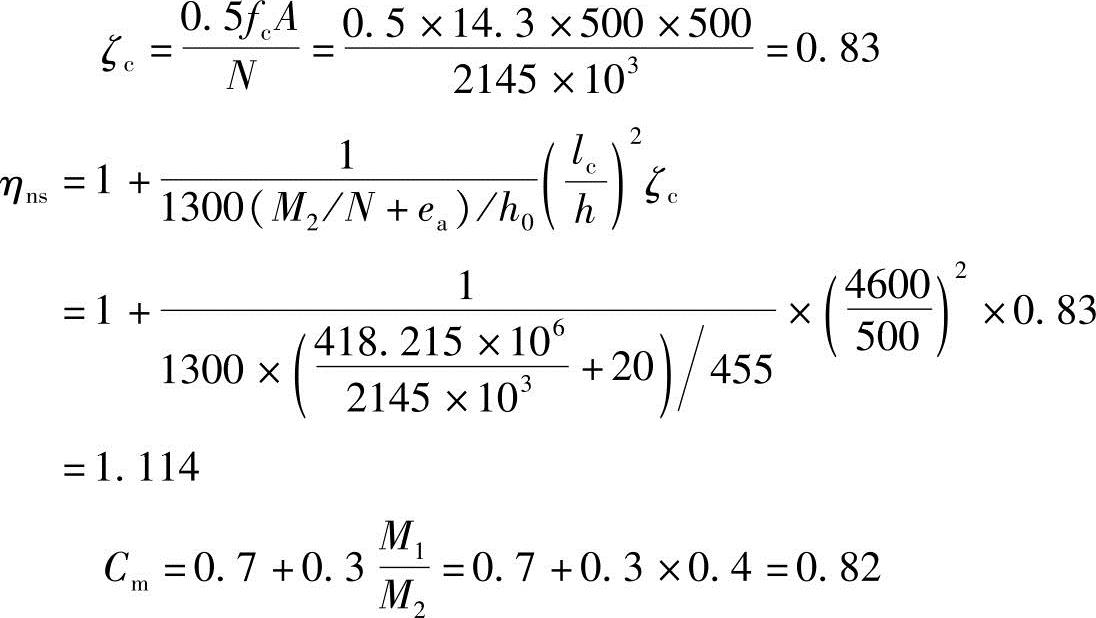
Cmηns=0.82×1.114=0.913<1.0,取Cmηns=1.0。
(3)两端弯矩异号的压弯构件
对于反弯点在中间区段(即端弯矩异号)的构件,《混凝土设计规范》第6.2.4条式(6.2.4-2)给出了两点规定。
1)当计算值Cm<0.7时,取Cm=0.7。
由《混凝土结构设计规范》式(6.2.4-2)不难看出,对于反弯点在中间区段(即端弯矩异号)的构件,Cm值将恒小于0.70。《混凝土结构设计规范》规定,当Cm计算值小于0.7时取0.7。这就等于规定,对于反弯点在中间区段的构件,取杆端弯矩绝对值较小者M1为零,这时构件将产生单曲率弯曲。显然,这一处理方案对构件的承载力而言,是偏于安全的。
2)ηnsCm<1.0时,取ηnsCm=1.0。
在有些情况下,例如在结构中常见的反弯点位于柱高、中部的偏压构件中,这时二阶效应虽能增大构件中部各截面的曲率和弯矩,但增大后的弯矩通常不可能超过柱两端截面的弯矩。这时,就会出现ηnsCm<1.0的情况。由《混凝土结构设计规范》式(6.2.4-4)可知,说明这时M小于M2。实际上,这时端弯矩M2为控制截面的弯矩。因此,《混凝土结构设计规范》规定,当ηnsCm<1.0时取1.0。
【例3.3.31】 计算控制截面的弯矩设计值
条件:钢筋混凝土框架柱,截面尺寸为b×h=400mm×450mm。柱的计算长度l0=6000mm。承受轴向压力设计值N=320kN。柱端弯矩设计值M1=-100kN·m,M2=300kN·m。混凝土强度等级为C30(fc=14.3N/mm2)。
提示:需考虑二阶效应的影响。
要求:计算控制截面的弯矩设计值。
解答:(1)按《混规》6.2.5条得
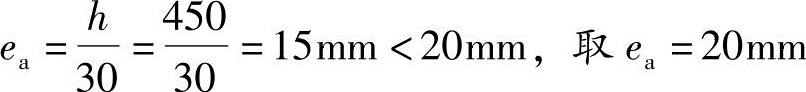
(2)按《混规》式(6.2.4-4)计算得
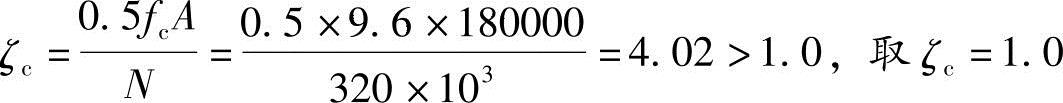
(3)按《混规》式(6.2.4-3)计算得
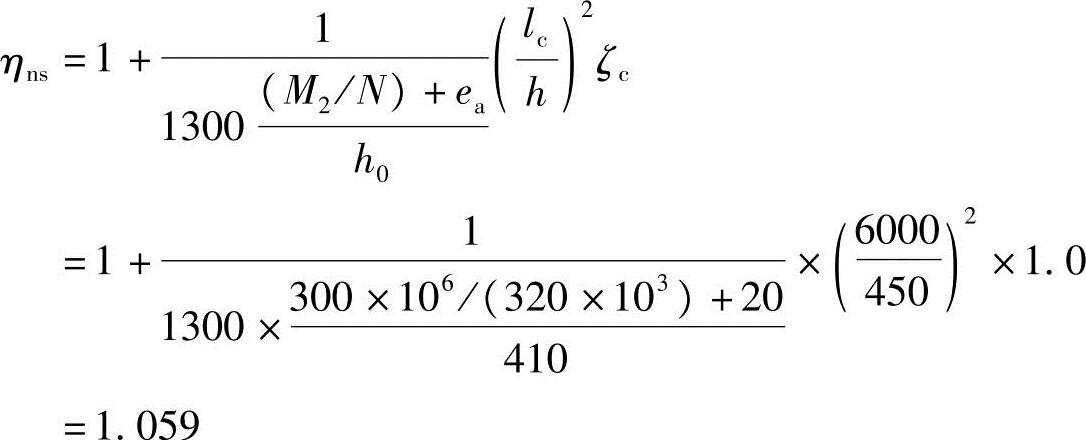
(4)按《混规》式(6.2.4-2)计算得
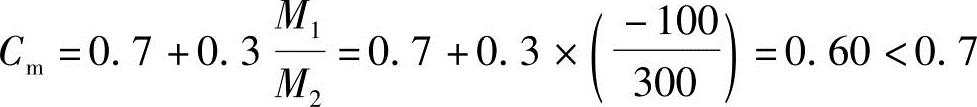
取Cm=0.7(即相当取M1=0)。
(5)按《混规》式(6.2.4-1)计算控制截面的弯矩设计值:
Cmηns=0.7×1.059=0.74<1.0,取Cmηns=1.0
M=ηnsCmM2=1.0×300=300kN·m
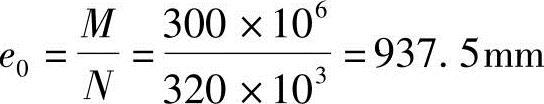
5.排架结构柱考虑二阶效应的弯矩设计值
《混凝土结构设计规范》规定:
B.0.4 排架结构柱考虑二阶效应的弯矩设计值可按下列公式计算:
M=ηsM0 (B.0.4-1)
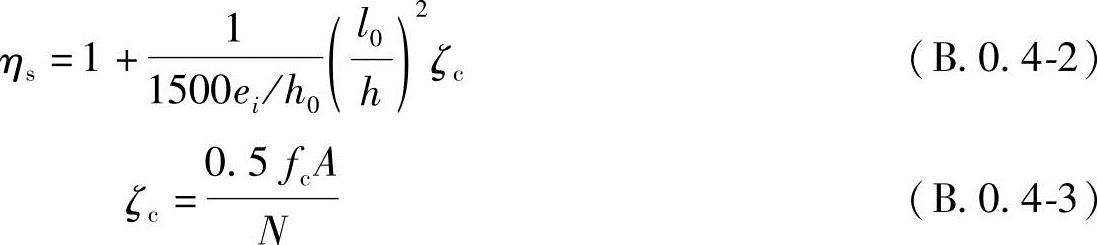
ei=e0+ea (B.0.4-4)
式中 ζc——截面曲率修正系数;当ζc>1.0时,取ζc=1.0;
ei——初始偏心距;
M0——一阶弹性分析柱端弯矩设计值;
e0——轴向压力对截面重心的偏心距,e0=M0/N;
ea——附加偏心距,按本规范第6.2.5条规定确定;
l0——排架柱的计算长度,按本规范表6.2.20-1取用;
h,h0——所考虑弯曲方向柱的截面高度和截面有效高度;
A——柱的截面面积,对于T形截面取:A=bh+2(bf-b)hf′。
【例3.3.32】 排架柱的纵向受压钢筋(2002年,因规范改版,本题已作相应调整。)
有一无吊车工业厂房,采用刚性屋盖,其铰接排架结构计算简图如图3.3.51所示。结构安全等级为二级,在垂直排架方向设有柱间支撑。混凝土强度等级为C25。纵向钢筋采用HRB400级钢筋。柱子截面尺寸为b×h=400mm×500mm,计算时假定as=as′=40mm,一阶弹性分析时柱子的轴向压力设计值为N=480kN,在排架方向为大偏心受压构件,对称配筋,e0=375mm>0.35h0。试问,柱子的纵向受压钢筋As′(mm2)与下列何项数值最为接近?
(A)1530 (B)1280
(C)753 (D)1153
答案:(D)
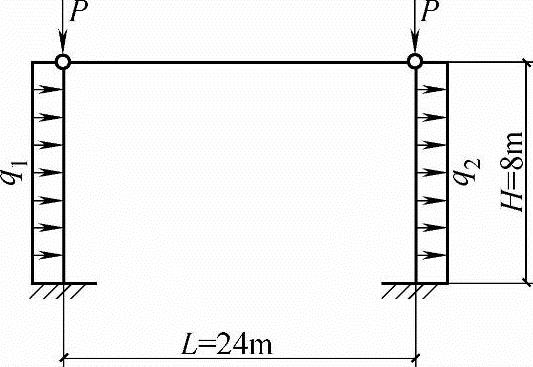
图 3.3.51
(1)根据《混规》6.2.5条,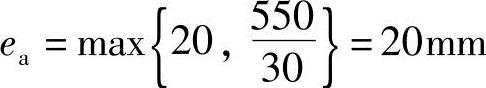
(2)根据《混规》表6.2.20-1,无吊车房屋柱、单跨、排架方向l0=1.5H=1.5×8=12m
(3)根据《混规》附录B.0.4条:
ei=e0+ea=375+20=395mm
h0=h-as=500-40=460mm
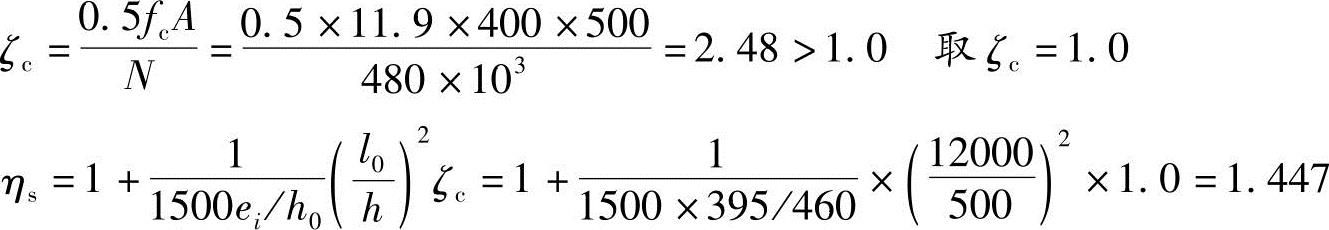
M0=e0N=0.375×480=180kN·m
M=ηsM0=1.447×180=260.46kN·m
(4)根据《混规》6.2.17条,大偏心受压:
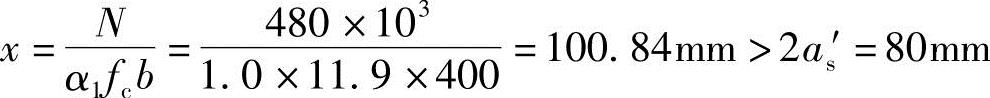
e0为轴向压力对截面重心的偏心距,取为M/N,当需要考虑二阶效应时,M为按《混规》第5.3.4条、第6.2.4条规定确定的弯矩设计值。
《混规》5.3.4条规定,混凝土结构的重力二阶效应可采用有限元分析方法计算,也可采用本规范附录B的简化方法。

(5)由《混规》表8.5.1,全部纵向钢筋最小配筋率为0.55%
As=0.55%×400×500=1100<2×1153=2306mm2
【分析】排架计算中开始按《混规》附录B.0.4得到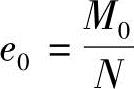 ,弯矩调整后,按《混规》6.2.17条得到
,弯矩调整后,按《混规》6.2.17条得到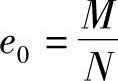 ,前后e0有变化。
,前后e0有变化。
(五)钢筋混凝土长柱的压弯承载力
1.考试要求
(1)《考试大纲》的要求:掌握
(2)“试题”回顾
1)配筋计算
【试题3.3.23】 柱子的纵向受压钢筋(2002年)
有一无吊车工业厂房,采用刚性屋盖,其铰接排架结构计算简图如图3.3.52所示。
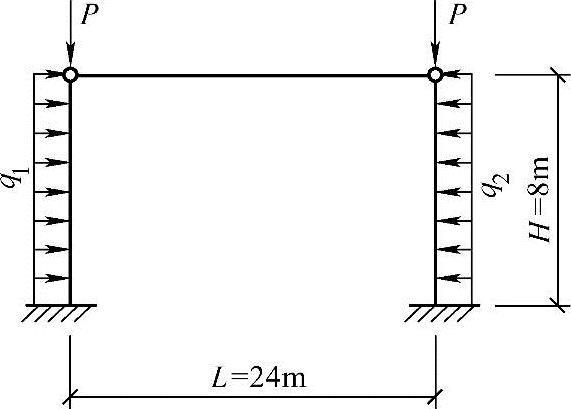
图 3.3.52
结构安全等级为二级,在垂直排架方向设有柱间支撑。混凝土强度等级为C20。纵向钢筋采用Ⅱ级钢。柱子截面尺寸b×h=400mm×550mm,计算时假定as=as′=40mm,假定柱子的轴向压力设计值为N=480kN,在排架方向为大偏心受压构件,偏心距增大系数η=1.43,对称配筋,e0=375mm>0.35h0,试问,柱子的纵向受压钢筋As′(mm2)与下列何项数值最为接近?
(A)1530 (B)1280 (C)753 (D)1041
【试题3.3.24】 对称配筋排架柱的纵向受压钢筋(2002年)
有一无吊车工业厂房,采用刚性屋盖,其铰接排架结构计算简图如图3.3.53所示。结构安全等级为二级,在垂直排架方向设有柱间支撑。混凝土强度等级为C20。纵向钢筋采用Ⅱ级钢,箍筋为Ⅰ级钢。柱子截面尺寸b×h=400mm×550mm,计算时假定as=as′=40mm。假定柱子的轴向压力设计值为N=480kN,在排架方向为大偏心受压构件,偏心距增大系数η=1.43,对称配筋,e0=375mm>0.35h0,试问柱子的纵向受压钢筋As′(mm2)与下列何项数值最为接近?
提示:1.在排架方向,柱按偏心受压构件计算其正截面强度,
且为对称配筋。
2.在垂直排架方向,柱按中心受压构件计算其正截面强度。
(A)1530 (B)1280 (C)753 (D)1041
图 3.3.53
【试题3.3.25】 对称配筋大偏心受压柱的最小纵向钢筋(2006年)
某一设有吊车的单层厂房柱(屋盖为刚性屋盖),上柱长Hu=3.5m,截面尺寸为400mm×400mm,下柱长Hl=10.0m,截面尺寸为400mm×900mm,上、下柱均为对称配筋,as=as′=40mm。混凝土强度等级为C25,纵向受力钢筋采用HRB335级热轧钢筋。当考虑横向水平地震作用组合时,在排架方向内力组合的最不利设计值为:上柱M=100kN·m,N=200kN;下柱M=700kN·m,N=1200kN。该柱下柱的偏心距增大系数η=1.2,承载力抗震调整系数γRE=0.8。已求得相对界限受压区高度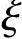 b=0.55,初始偏心距ei=566mm,混凝土受压区高度x=236.6mm。试问,当采用对称配筋时,该下柱的最小纵向配筋面积As=As′(mm2)应与下列何项数值最为接近?
b=0.55,初始偏心距ei=566mm,混凝土受压区高度x=236.6mm。试问,当采用对称配筋时,该下柱的最小纵向配筋面积As=As′(mm2)应与下列何项数值最为接近?
(A)854.9 (B)1653 (C)1866 (D)2686
【试题3.3.26】 对称配筋框架柱的最小纵向钢筋(2008年)
某钢筋混凝土框架结构多层办公楼,安全等级为二级,框架抗震等级为二级。该房屋各层层高均为3.6m,首层地面标高为±0.000m,基础顶面标高为-1.000m,框架柱截面尺寸b×h=500mm×500mm,混凝土强度等级为C30,柱纵向钢筋采用HRB335级钢筋(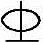 ),柱箍筋采用HPB235级钢筋(
),柱箍筋采用HPB235级钢筋(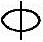 ),as=as′=45mm。该框架底层中柱在考虑地震作用组合且经调整后的最不利设计值为:N=1920kN,M=490kN·m,初始偏心距ei=275mm,轴向压力偏心距增大系数η=1.2,承载力抗震调整系数γRE=0.8。试问,当采用对称配筋时,该框架柱最小纵向配筋面积As=As′(mm2)与下列何项数值最为接近?
),as=as′=45mm。该框架底层中柱在考虑地震作用组合且经调整后的最不利设计值为:N=1920kN,M=490kN·m,初始偏心距ei=275mm,轴向压力偏心距增大系数η=1.2,承载力抗震调整系数γRE=0.8。试问,当采用对称配筋时,该框架柱最小纵向配筋面积As=As′(mm2)与下列何项数值最为接近?
提示: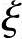 bh0=250mm。
bh0=250mm。
(A)1885 (B)2338 (C)3345 (D)4008
2)承载力计算
【试题3.3.27】~【试题3.3.28】 (2009年)
某钢筋混凝土偏心受压柱,截面尺寸及配筋如图3.3.54所示,混凝土强度等级为C30,纵筋采用HRB335级钢筋。已知轴向压力设计值N=300kN,偏心距增大系数η=1.16,as=as′=40mm。
【试题3.3.27】 大偏压柱的偏心距es′
当按单向偏心受压验算承载力时,试问,轴向压力作用点至受压区纵向普通钢筋合力点的距离es′(mm)最大值,应与下列何项数值最为接近?
(A)280 (B)290 (C)300 (D)310
【试题3.3.28】 大偏压柱的受弯承载力
假定es′=305mm,试问,按单向偏心受压计算时,该柱受弯承载力设计值M(kN·m)与下列何项数值最为接近?
(A)114 (B)120 (C)130 (D)140
【试题3.3.29】~【试题3.3.30】 (2010年)
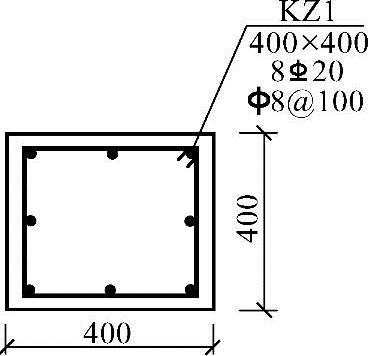
图 3.3.54
某钢筋混凝土多层框架结构的中柱,剪跨比λ>2,截面尺寸及计算配筋如图3.3.55所示,抗震等级为四级,混凝土强度等级为C30。考虑水平地震作用组合的底层柱底轴向压力设计值N1=300kN,二层柱底轴向压力设计值N2=225kN。纵向受力钢筋采用HRB335级钢筋,箍筋采用HPB235级钢筋,as=as′=40mm,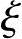 b=0.55。
b=0.55。
【试题3.3.29】 大偏压柱的偏心距es′
试问,当计算该底层中柱下端单向偏心受压的抗震受弯承载力设计值时,对应的轴向压力作用点至受压区纵向钢筋合力点的距离es′(mm),与下列何项数值最为接近?
(A)237 (B)296 (C)316 (D)492
【试题3.3.30】 偏压柱的受弯承载力
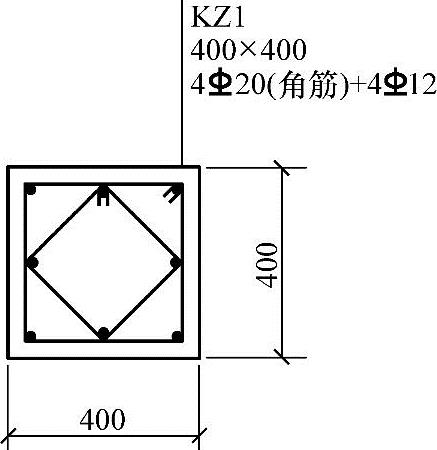
图 3.3.55
假设图3.3.55所示的柱为二层中柱,其柱底轴向压力作用点至受压区纵向钢筋合力点的距离es′=420mm,偏心距增大系数η=1.16。试问,该柱下端按单向偏心受压计算时的抗震受弯承载力设计值M(kN·m),与下列何项数值最为接近?
(A)95 (B)108 (C)113 (D)117
2.《混凝土结构设计规范》的规定和算例
《混凝土结构设计规范》规定:
6.2.17 矩形截面偏心受压构件正截面受压承载力应符合下列规定(图6.2.17):
N≤α1fcbx+fy′As′-σsAs-(σp′0-fp′y)Ap′-σpAp (6.2.17-1)
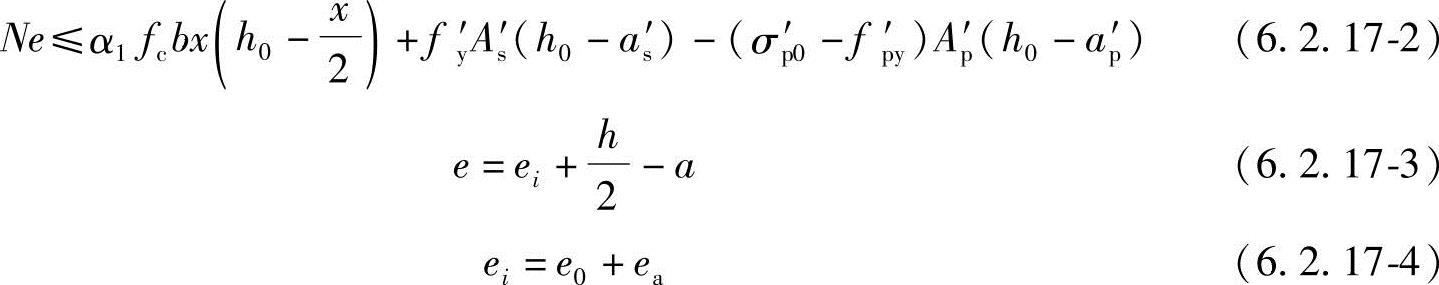
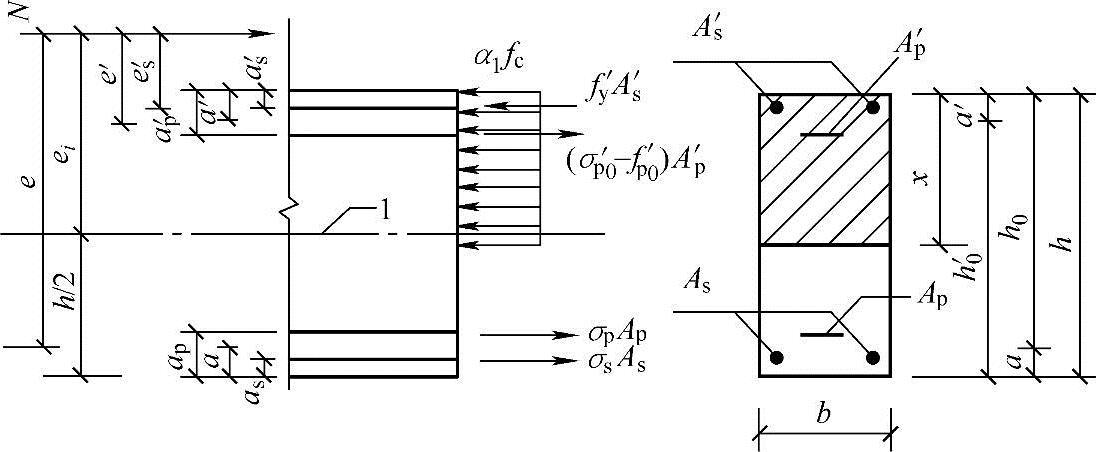
图6.2.17 矩形截面偏心受压构件正截面受压承载力计算
1—截面重心轴
式中 e0——轴向压力对截面重心的偏心距,取为M/N,当需要考虑二阶效应时,M为按本
规范第5.3.4条、第6.2.4条规定确定的弯矩设计值。
5.3.4 当结构的二阶效应可能使作用效应显著增大时,在结构分析中应考虑二阶效应的不利影响。
6.2.4 除排架结构柱外,其他偏心受压构件考虑轴向压力在挠曲杆件中产生的二阶效应后控制截面的弯矩设计值,应按下列公式计算:
M=CmηnsM2 (6.2.4-1)
(1)长柱的承载力计算
在图3.3.56所示的N/M坐标图内表示2根截面尺寸相同、长细比不同的偏压柱的加载路线图,作用于这2根柱两端的轴压力N和初始偏心距ei均是相同的。
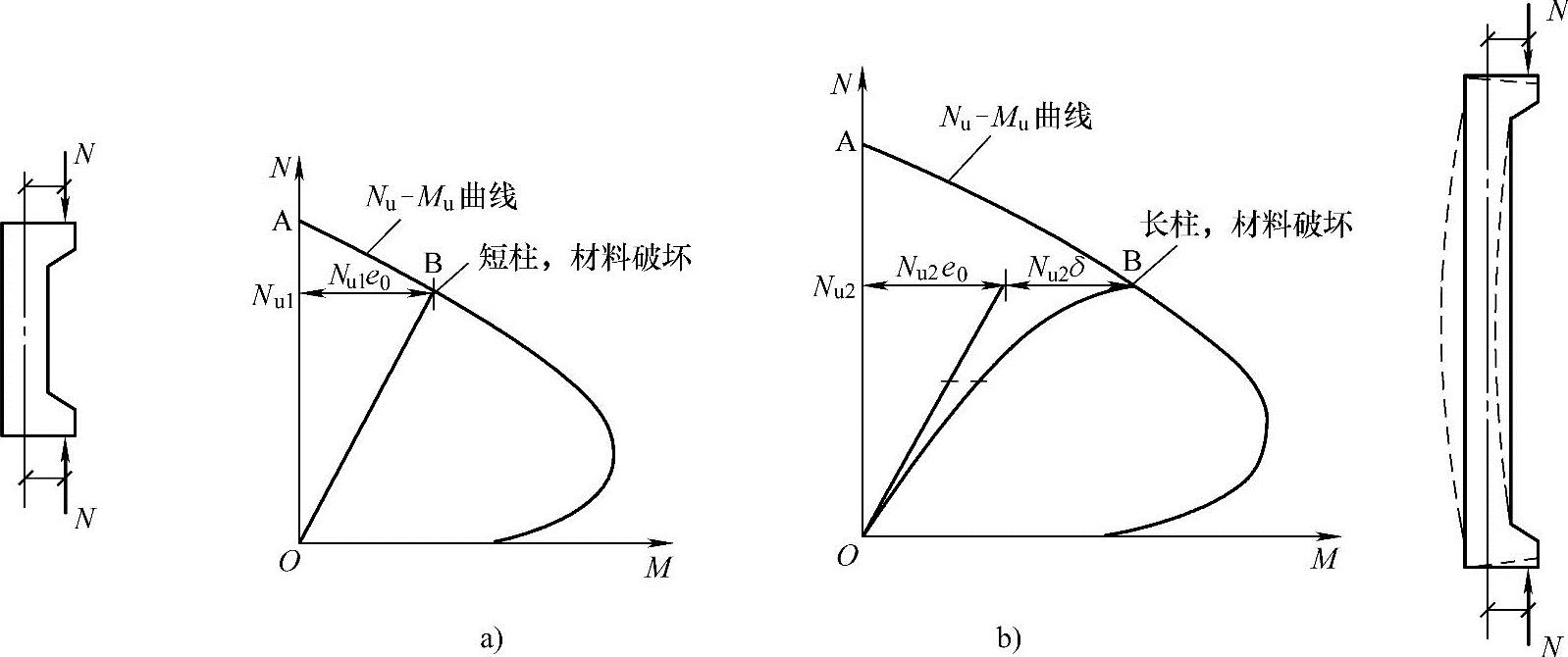
图 3.3.56
左柱是短柱,未出现二阶弯矩,作用于柱高全长的弯矩均是M=Nei,其加载路线是条直线,与坐标轴间的夹角是不变的。所以承载力计算即取柱端截面的内力M、N进行。
右柱是长柱,出现二阶弯矩,柱高中间的最大弯矩是M=Nei+Nδ,其加载路线不是条直线,与坐标轴间的夹角是变化的,柱端截面承受的弯矩是M=Nei,而柱高中间的弯矩已提高Nδ,所以承载力计算时要取弯矩最大的截面内力进行。当已知柱端内力N、M2进行配筋计算时,要采用考虑二阶效应后控制截面的弯矩设计值M=CmηnsM2。当已知纵筋面积As、As′,根据承载力公式所求得的承载力是柱高、中部最大弯矩截面的承载力,要计算该柱承载力时,尚须还原到柱端的弯矩值M2。已知柱端内力M2,计算考虑二阶效应后控制截面的弯矩设计值M=CmηnsM2的算例前面已经讲述,这里仅讲述求得柱高中部的承载力还原到柱端的弯矩值M2的算例。
【例3.3.33】 已知M,求M2
条件:已知偏心受压柱b=400mm,h=600mm,混凝土强度等级为C40,钢筋HRB400。构件计算长度lc=4m,作用在柱上的轴向力设计值N=1200kN,两端弯矩相等(M1/M2=1.0)。已知控制截面能承受的弯矩设计值M=483.6kN·m。
要求:试求柱端能承担的弯矩设计值M2。
解答:M1/M2=1.0>0.9,需考虑二阶弯矩的影响。
按《混规》式(6.2.4-4)得
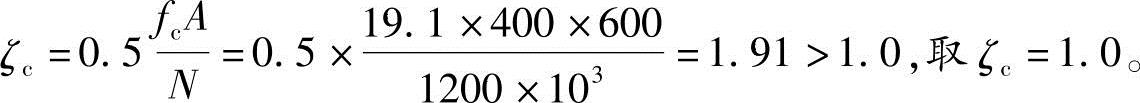
按《混规》式(6.2.4-3)得
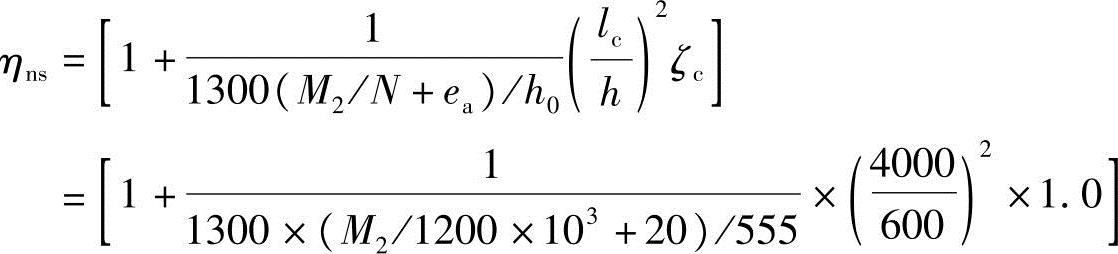
按《混规》式(6.2.4-2)得
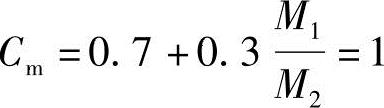
按《混规》式(6.2.4-1)得
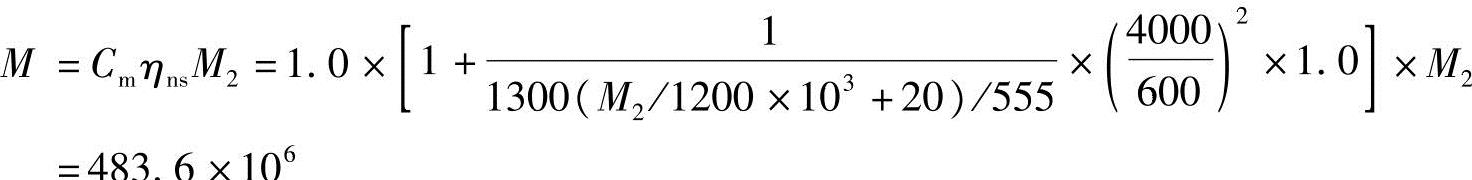
解得,柱端弯矩M2=461.93kN·m
(2)钢筋混凝土长柱配筋计算的算例
【例3.3.34】 长柱配筋计算(2as′<x<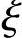 bh0)
bh0)
条件:某钢筋混凝土偏心受压柱,承受轴向压力设计值N=500kN,柱端较大弯矩设计值M2=380kN·m,截面尺寸为b×h=400mm×450mm,as=as′=40mm,柱的计算长度lc=5m,采用C30混凝土和HRB400钢筋(按两端弯矩相等M1/M2=1的框架柱考虑)。
要求:进行截面对称配筋设计。
解答:(1)确定设计参数
C30混凝土:α1=1.0,β1=0.8,fc=14.3N/mm2。
HRB400钢筋:fy′=fy=360N/mm2,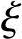 b=0.518。
b=0.518。
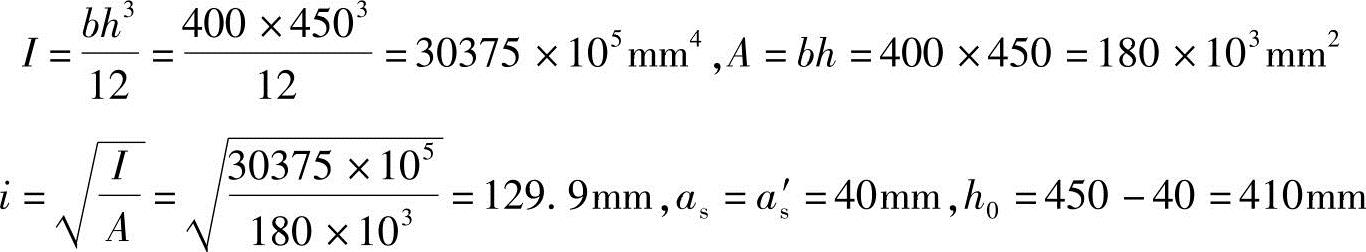
(2)求框架柱设计弯矩M
由于M1/M2=1,因此,需要考虑附加弯矩影响:

得框架柱设计弯矩为
M=CmηnsM2=1×1.05×380=399kN·m
(3)判别大、小偏心受压
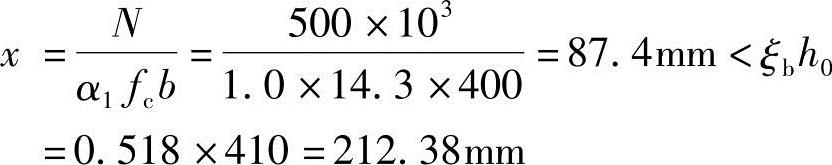
故属于大偏心受压,且x=87.4mm>2as′=2×40=80mm。
(4)计算As′和As

(5)选配钢筋并验算配筋率,绘截面配筋图3.3.57。
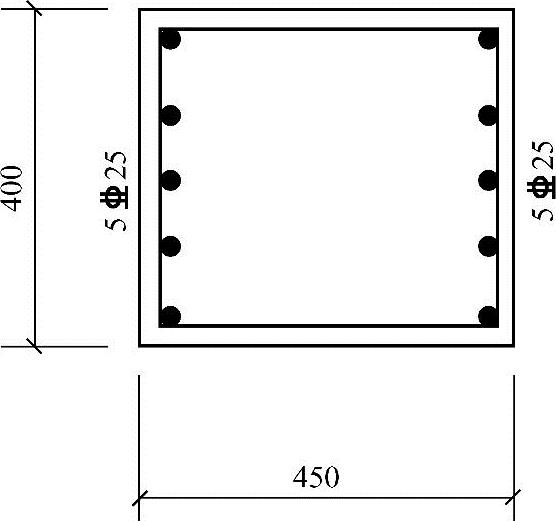
图 3.3.57
每侧各选配5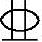 25(As′=As=2454mm2)。
25(As′=As=2454mm2)。
全部纵筋配筋率为:
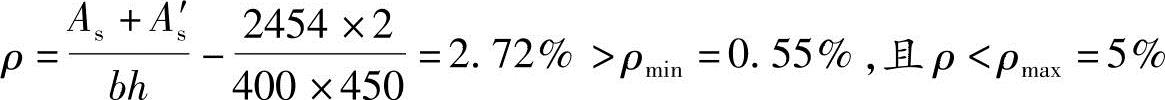
满足要求。
【例3.3.35】 长柱配筋计算(x<2as′)
条件:钢筋混凝土偏心受压柱,截面尺寸b=500mm,h=500mm,as=a′s=50mm。截面承受轴向压力设计值N=200kN,柱顶截面弯矩设计值M1=280kN·m,柱底截面弯矩设计值M2=300kN·m。柱挠曲变形为单曲率。弯矩作用平面内柱上下两端的支撑长度为4.2m,混凝土强度等级为C35,纵筋采用HRB400级钢筋。
要求:采用对称配筋,求受拉和受压钢筋。
解答:
由已知条件查得:fy=360N/mm2, fy′=360N/mm2;fc=16.7N/mm2,h0=h-as=500-50=450mm
弯矩作用平面内柱计算长度lc=4.2m。
(1)判断构件是否考虑附加弯矩杆端弯矩比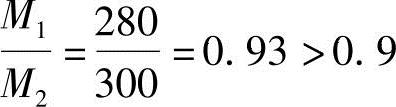 ,所以应考虑杆件自身挠曲变形的影响。
,所以应考虑杆件自身挠曲变形的影响。
(2)计算构件弯矩设计值

由于Cmηns=0.995<1,取Cmηns=1,则
M=CmηnsM2=1×300=300kN·m
(3)判别偏压类型
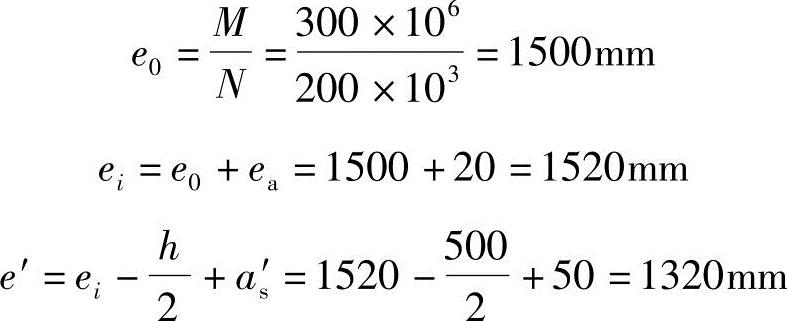
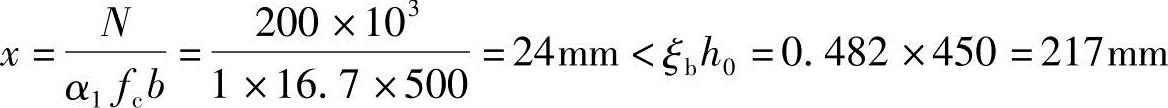
判定为大偏心受压,但x<2as′=2×50=100mm,近似取x=2as′。
(4)计算钢筋面积
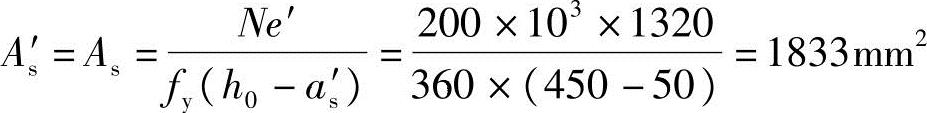
选5 22(As=As′=1900mm2),截面总配筋率为
22(As=As′=1900mm2),截面总配筋率为
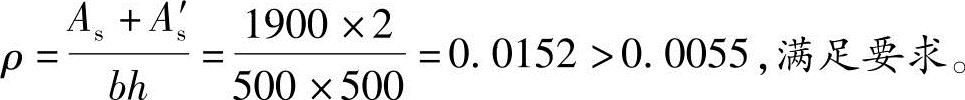
【例3.3.36】 长柱配筋计算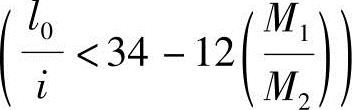
条件:钢筋混凝土框架柱,截面尺寸b×h=400mm×450mm。柱的计算长度l0=4000mm,as=as′=40mm。承受轴向压力设计值N=320kN,柱端弯矩设计值M1=-100kN·m,M2=300kN·m。混凝土强度等级为C30(fc=14.3N/mm2),h0=h-as=450-40=410mm,采用HRB400级钢筋(fy=fy′=360N/mm2)。
要求:采用对称配筋,试确定纵向钢筋截面面积As=As′。
解答:(1)判断是否需考虑二阶效应
A=b×h=400×450=180000mm2
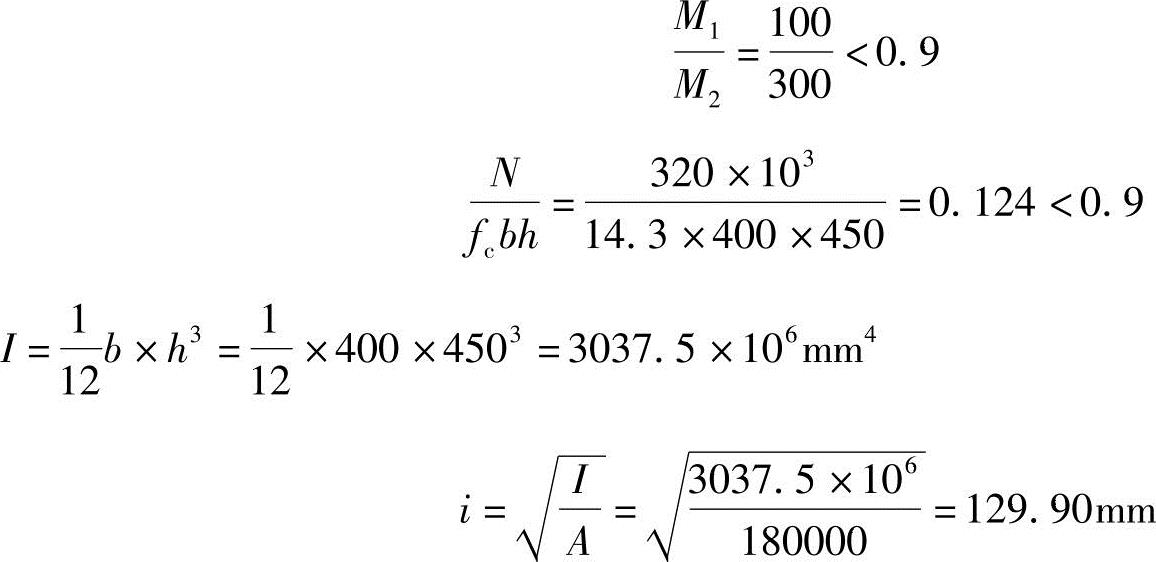
因为
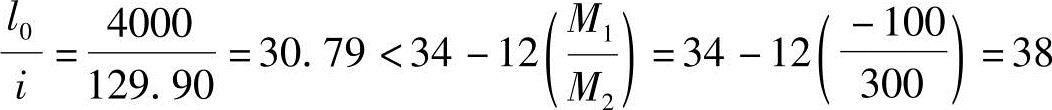
故可不考虑二阶效应的影响。
(2)判别大小偏心
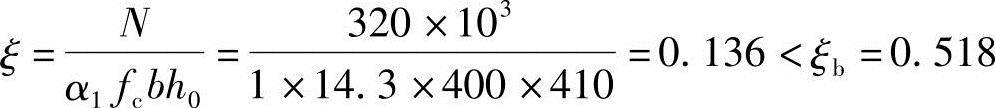
属于大偏心受压,且
x=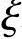 h0=0.136×410=55.76mm<2as′=2×40=80mm
h0=0.136×410=55.76mm<2as′=2×40=80mm
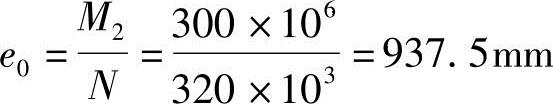

(3)计算配筋
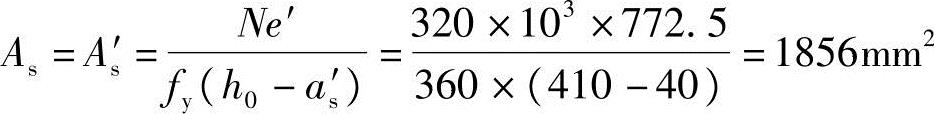
截面每侧各配置4 25(As=1964mm2),配筋如图3.3.58所示,则有
25(As=1964mm2),配筋如图3.3.58所示,则有
3.钢筋混凝土长柱承载力计算案例
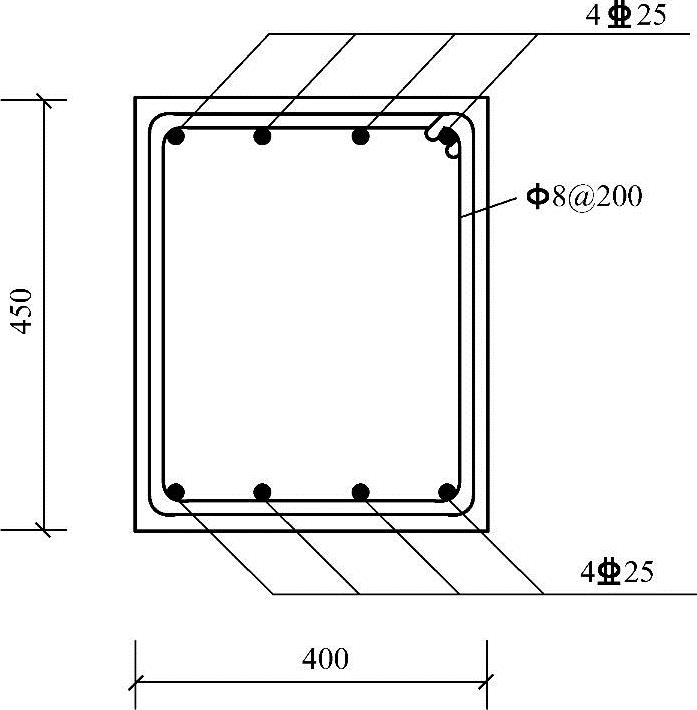
图 3.3.58
【例3.3.37】 验算截面承载力
条件:钢筋混凝土偏心受压柱,截面尺寸b×h=300mm×400mm,as=a′s=50mm。柱承受轴向压力设计值N=254kN,柱顶截面弯矩设计值M1=122kN·m,柱底截面弯矩设计值M2=135kN·m。柱挠曲变形为单曲率。弯矩作用平面内柱上下两端的支撑长度为3.5m,混凝土强度等级为C30,纵筋采用HRB400级钢筋。受压钢筋为3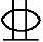 16(A′s=603mm2),受拉钢筋为4
16(A′s=603mm2),受拉钢筋为4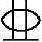 20(As=1256mm2)。
20(As=1256mm2)。
要求:验算截面是否满足承载力的要求。
解答:由已知查表得:fy=fy′=360N/mm2;fc=14.3N/mm2,h0=h-as=400-50=350mm;
弯矩作用平面内柱计算长度l0=3.5m。
(1)判断构件是否考虑附加弯矩杆端弯矩比: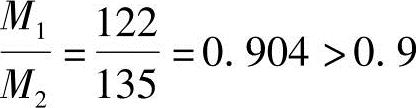 应考虑杆件自身挠曲变形的影响。
应考虑杆件自身挠曲变形的影响。

M=CmηnsM2=0.971×1.04×135=136.33kN·m
(2)判别偏压类型
用试算法判为大偏心受压构件,具体过程略。
(3)计算截面能承受的偏心压力设计值Nu
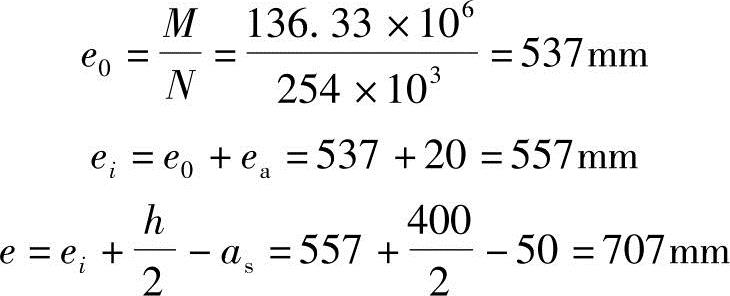
将已知条件代入式
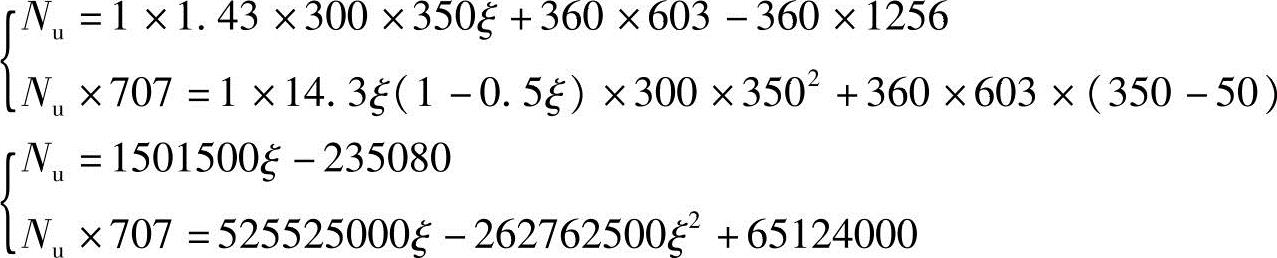
解得:
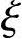 =0.3659<
=0.3659<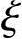 b=0.518
b=0.518
Nu=314.34kN>254kN
【例3.3.38】、【例3.3.39】 (2010年,因规范改版,本题已作相应调整。)
某钢筋混凝土多层框架结构的中柱,剪跨比λ>2,截面尺寸及计算配筋如图3.3.59所示,抗震等级为四级,混凝土强度等级为C30。考虑水平地震作用组合的底层柱底轴向压力设计值N1=300kN,二层柱底轴向压力设计值N2=225kN。纵向受力钢筋采用HRB400级钢筋,箍筋采用HRB300级钢筋,as=as′=40mm,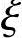 b=0.518。
b=0.518。
【例3.3.38】 大偏压柱的偏心距es′
试问,当计算该底层中柱下端单向偏心受压的抗震受弯承载力设计值,对应的轴向压力作用点至受压区纵向钢筋合力点的距离es′(mm),与下列何项数值最为接近?
(A)237 (B)296
(C)316 (D)380
答案:(D)
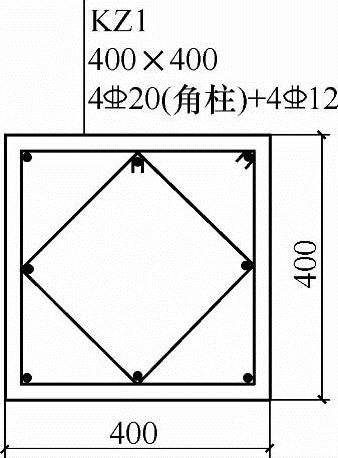
图 3.3.59
(1)根据《混规》表11.1.6,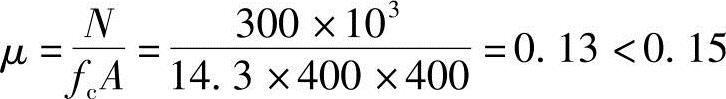 ,γRE=0.75
,γRE=0.75
(2)根据《混规》6.2.17条公式(6.2.17),假定为大偏心受压:
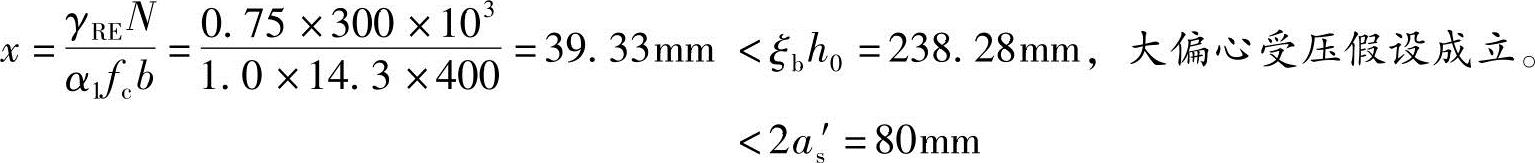
(3)根据《混规》6.2.17-2条,当x<2as′时,应将本规范公式(6.2.14)中的M以es′代替,此处,es′为轴向压力作用点至受压区纵向普通钢筋合力点的距离;初始偏心距应按公式(6.2.17-4)确定。
(4)根据《混规》6.2.14条,M≤fyAs(h-as-as′),根据6.2.17-2条代入M=Nes′。式中2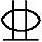 20+1
20+1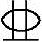 12,面积为741.1mm2,代入公式:
12,面积为741.1mm2,代入公式:
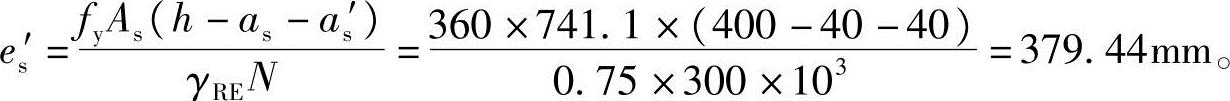
【例3.3.39】 偏压柱的受弯承载力
假设图3.3.59中所示的柱为二层中柱,其柱底轴向压力作用点至受压区纵向钢筋合力点的距离es′=420mm,考虑二阶效应的弯矩增大系数Cmηns=1.16,试问,该柱下端按一阶弹性分析时的单向偏心受压计算的抗震受弯承载力设计值M(kN·m),与下列何项数值最为接近?
(A)95 (B)108 (C)113 (D)117
答案:(B)
(1)根据《混规》6.2.17-2条,es′为轴向压力作用点至受压区纵向普通钢筋合力点的距离。
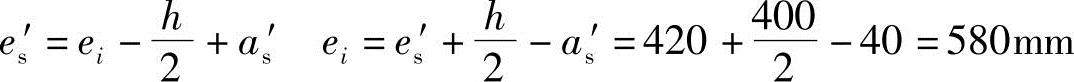
(2)根据《混规》6.2.5条,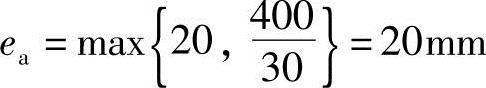
(3)根据《混规》6.2.17条:
e0=ei-ea=580-20=560mm
M=Ne0=225×0.56=126kN·m
(4)根据《混规》6.2.4条,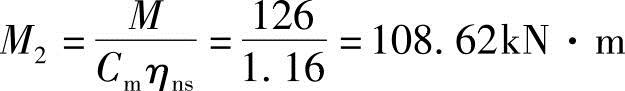 。
。
(六)工形截面偏压构件
1.考试要求
(1)《考试大纲》的要求:掌握
(2)“试题”回顾
【试题3.3.31】 下柱配筋计算(2001年)
假定厂房柱采用C30级混凝土,主筋为Ⅱ级钢筋,下柱为I形截面,其截面尺寸如图3.3.60所示;截面的有效高度h0=960mm,构件的截面面积A=1.975×103mm2;截面内力为M=563.75kN·m,N=696.48kN;对称配筋,系大偏心受压构件。假定η=1.066。试指出其计算配筋量As=As′(mm2)的数值与下列何项数值最为接近?
(A)1015 (B)1085
(C)983.8 (D)973
【试题3.3.32】 工形截面偏压构件(2009年)
某钢筋混凝土单层单跨厂房(有吊车,屋面为刚性屋盖),其排架柱的上柱Hu=3.3m,下柱Hl=11.5m,上、下柱截面尺寸如图3.3.61所示。当考虑横向水平地震作用组合时,在排架方向内力组合的最不利设计值为:上柱M=110kN·m,N=250kN;下柱M=580kN·m,N=730kN。混凝土强度等级为C30,纵向受力钢筋采用HRB335级钢筋( );对称配筋,as=as′=40mm。
);对称配筋,as=as′=40mm。
假设该单层厂房柱的下柱在排架方向的偏心距增大系数η=1.15,初始偏心距ei=825mm,承载力抗震调整系数γRE=0.8,其截面及配筋如图3.3.61所示。试问,该下柱最小纵向配筋面积As=As′(mm2),应与以下何项数值最为接近?
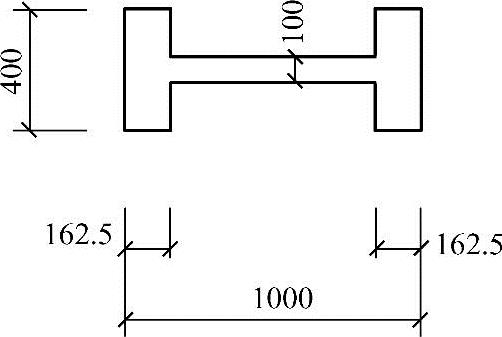
图 3.3.60
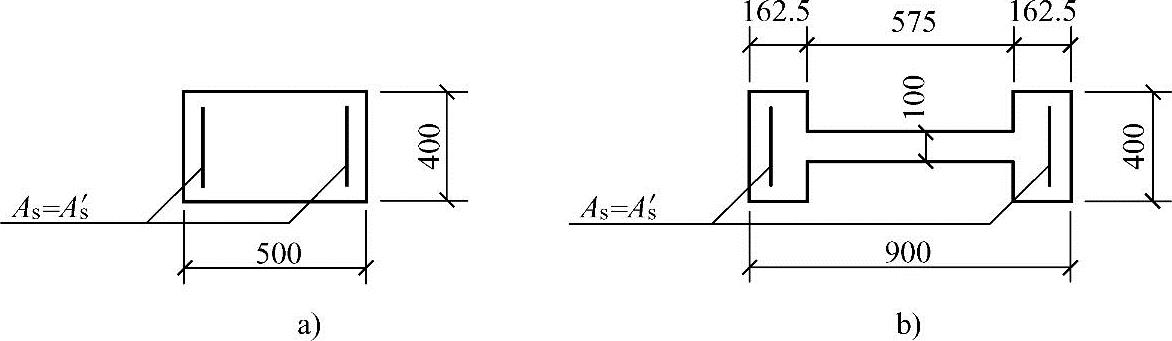
图 3.3.61
a)上柱截面 b)下柱截面
提示: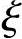 bh0=473mm。
bh0=473mm。
(A)864 (B)1308 (C)1671 (D)2114
2.《混凝土结构设计规范》的规定和算例
《混凝土结构设计规范》规定:
6.2.18 工形截面偏心受压构件的受压翼缘计算宽度bf′按本规范第6.2.12条确定,其正截面受压承载力应符合下列规定:
1.当受压区高度x不大于hf′时,应按宽度为受压翼缘计算宽度bf′的矩形截面计算。
2.当受压区高度x大于hf′时(图6.2.18),应符合下列规定
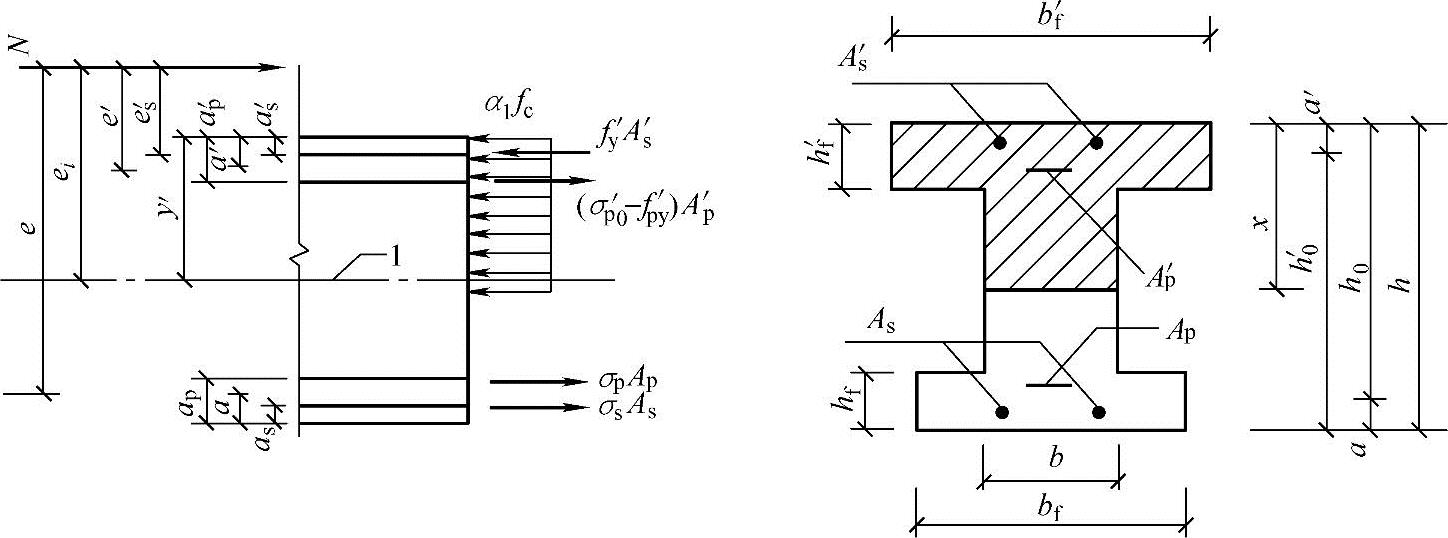
图6.2.18 工形截面偏心受压构件正截面受压承载力计算
1—截面重心轴
N≤α1fc[bx+(bf′-b)hf′]+fy′As′-σsAs-(σp′0-fp′y)Ap′-σpAp (6.2.18-1)
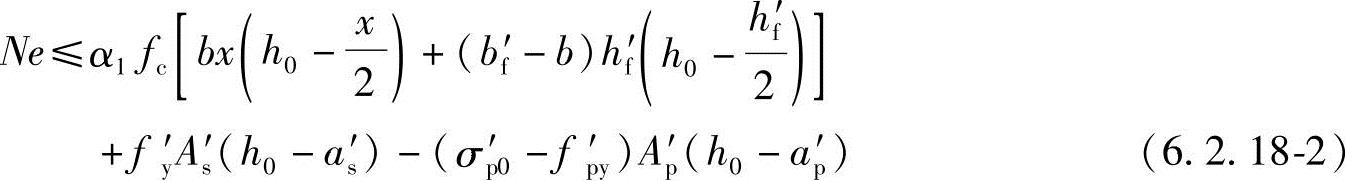
公式中的钢筋应力σs、σp以及是否考虑纵向受压普通钢筋的作用,均应按本规范第6.2.17条的有关规定确定。
3.当x大于(h-hf)时,其正截面受压承载力计算应计入受压较小边翼缘受压部分的作用,此时,受压较小边翼缘计算宽度bf应按本规范第6.2.12条确定。
注:对仅在离轴向压力较近一侧有翼缘的T形截面,可取bf为b;对仅在离轴向压力较远一侧有翼缘的倒T形截面,可取bf′为b。
【例3.3.40】 工形截面偏压构件(2009年,因规范改版,本题已作相应调整。)
某钢筋混凝土单层单跨厂房(有吊车,屋面为刚性屋盖),其排架柱的上柱Hu=3.3m,下柱Hl=11.5m,上、下柱截面尺寸如图3.3.62所示。当考虑横向水平地震作用组合的一阶弹性分析时,在排架方向内力组合的最不利设计值为:上柱M=110kN·m,N=250kN;下柱M=580kN·m,N=730kN。混凝土强度等级为C30,纵向受力钢筋采用HRB400级钢筋(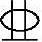 ),对称配筋,as=as′=40mm。
),对称配筋,as=as′=40mm。
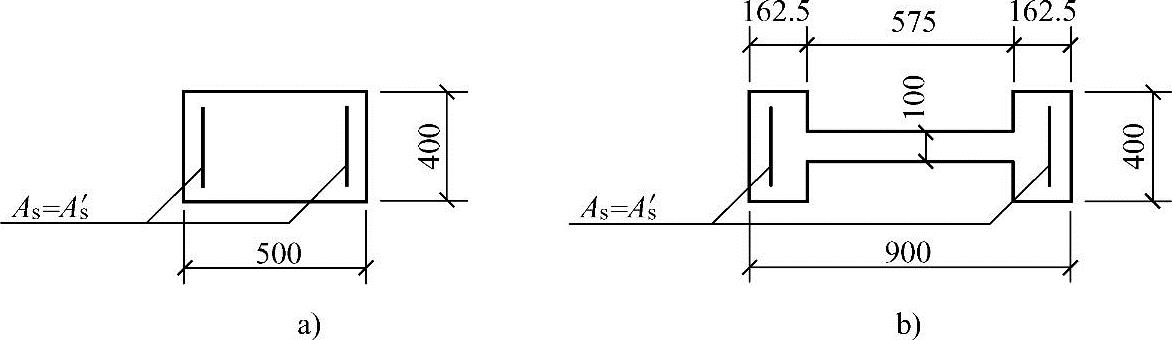
图 3.3.62
a)上柱截面 b)下柱截面
假设下柱在排架方向考虑P-Δ效应增大系数为1.17,承载力抗震调整系数γRE=0.8,其截面如图3.3.62b所示。试问,该下柱最小纵向配筋面积As=As′(mm2),应与以下何项数值最为接近?
(A)864 (B)1109 (C)1671 (D)2114
答案:(B)
(1)根据《混规》附录B.0.4条,M=1.17×580=678.6kN·m
(2)假定受压区高度小于受压翼缘高度
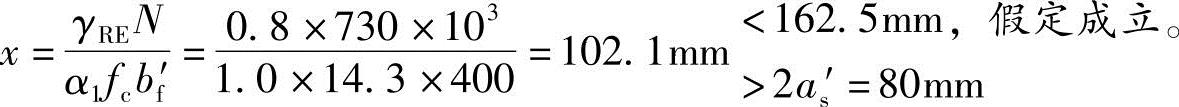
(3)根据《混规》6.2.5条,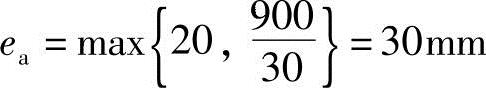
(4)根据《混规》6.2.17条:

(5)根据《混规》表8.5.1,全部纵向钢筋最小配筋率为0.55%全截面面积:A=2×162.5×(400-100)+900×100=187500mm2
As=0.55%×187500=937.5<2×1109=2218mm2。
【例3.3.41】 工形柱的配筋计算(x>hf′,x≤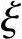 bh0)
bh0)
条件:已知某单层工业厂房的I形截面边柱,柱截面控制内力N=853.5kN,考虑二阶效应的Mmax=38.92kN·m,截面尺寸如图3.3.63所示。混凝土强度等级为C35,采用HRB400级钢筋,对称配筋。安全等级为二级,环境类别为二b类。
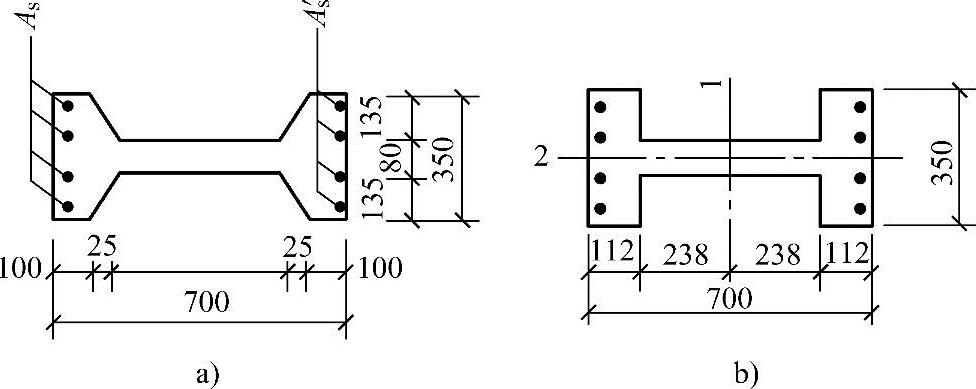
图3.3.63 截面尺寸和配筋布置
要求:求所需钢筋截面面积As=As′。
解答:(1)查《混规》表8.2.1得柱的混凝土保护层厚度c=35mm;
设纵向钢筋的合力作用点到近边的距离as=45mm。h0=h-as=700-45=655mm
(2)查《混规》得 fc=16.7N/mm2,fy=fy′=360N/mm2;α1=1.0,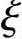 b=0.518
b=0.518
(3)截面形状的简化
计算时将翼缘的形状简化成矩形面积,如图3.3.63b所示。
(4)求e0
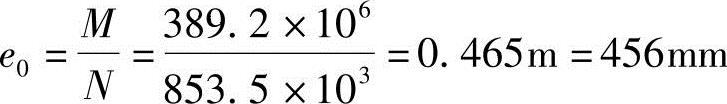
按《混规》第6.2.5条,附加偏心距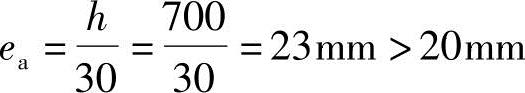 ,取ea=23mm。
,取ea=23mm。
(5)求ei,e
按《混规》式(6.2.17-4),ei=e0+ea=456+23=479mm
按《混规》式(6.2.17-3)得:
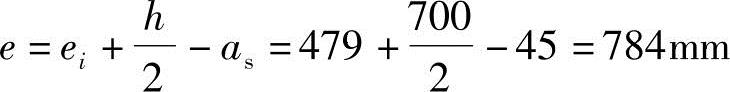
(6)求As,min
查《混规》表8.5.1,受压构件一侧纵向钢筋的ρmin=0.2%
As,min=ρminA=0.2%×116480=233mm2
(7)求x
先按大偏心受压计算。用《混规》式(6.2.17-1),取b=bf′,得:
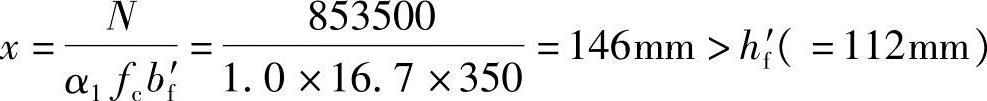
此时,中和轴在腹板内,用《混规》式(6.2.18-1)计算得:
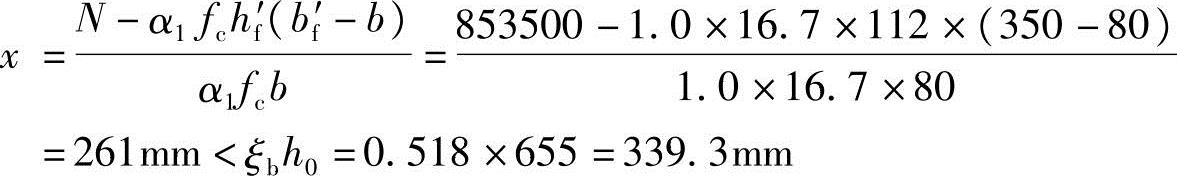
原假定按大偏心受压可以。
(8)求As=As′
根据《混规》式(6.2.18-2)得:
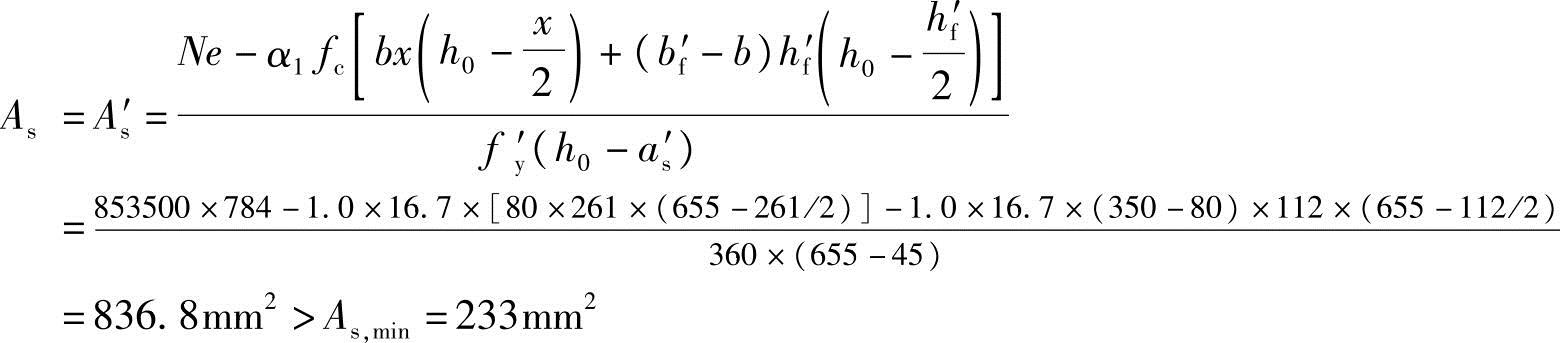
选用4 18钢筋,As=As′=1017mm2。
18钢筋,As=As′=1017mm2。
【例3.3.42】 工字形柱的配筋计算(x<2as′)
条件:已知对称工字形截面如图3.3.64所示,bf=bf′=400mm,b=100mm,h=600mm,hf′=hf=100mm,as=as′=45mm,混凝土强度等级为C30,fc=14.3N/mm2,采用HRB400级钢筋,fy=360N/mm2,承受轴向压力设计值N=300kN,考虑二阶效应的弯矩设计值M=210kN·m。
要求:求对称配筋的截面面积。
解答:(1)求x
由于是对称配筋,故As=As′,fy=fy′,先按b=bf′的矩形截面偏压考虑。
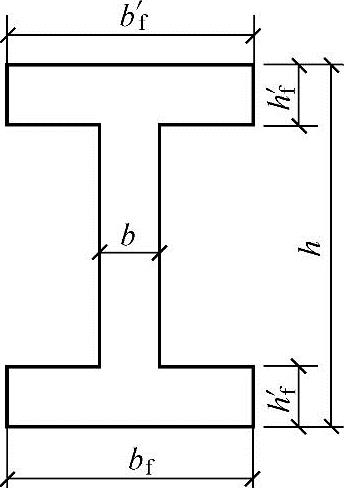
图 3.3.64
h0=h-as=600-45=555mm
A=100×600+2(400-100)×100=120000mm2
由《混规》式(6.2.17-1)得:
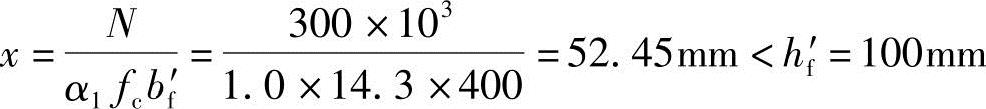
可按b=bf′的矩形截面计算,得:
x=52.45mm<xb=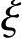 bh0=0.518×(600-45)=287.5mm
bh0=0.518×(600-45)=287.5mm
为大偏心受压构件
且 x=52.45mm<2as′=2×45=90mm
(2)求偏心距
e0=M/N=210×106/300×103=700mm
ea=h/30=20mm,取ea=20mm
ei=e0+ea=700+20=720mm
(3)求As和As′
取x=2as′=2×45=90mm,由《混规》式(6.2.14)得:
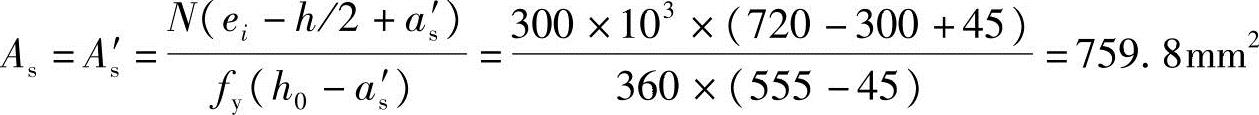
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




