T形梁受弯承载力分析及计算

（一）T形梁的受压翼缘计算宽度

1.考试要求

（1）《考试大纲》规定：掌握

（2）“试题”回顾

【试题3.2.15】 T形梁受压翼缘计算宽度（1998年）

肋形楼盖结构剖面如图3.2.18所示，梁的计算跨度l₀=10m，其翼缘计算宽度b_f（mm）应按以下何项取值？

（A）2000 （B）920 （C）200 （D）3300

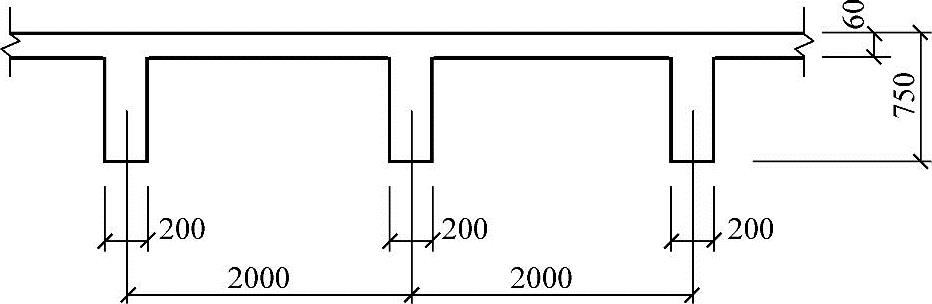
图 3.2.18

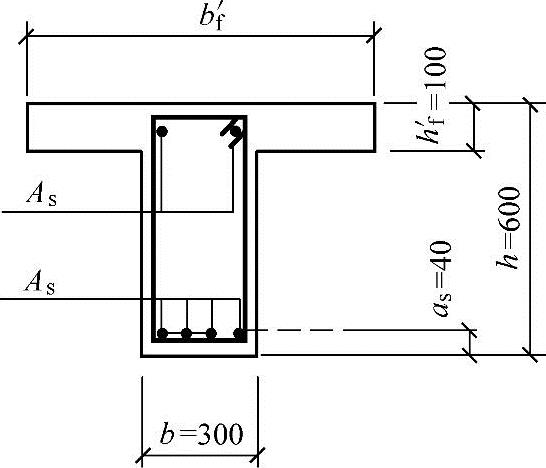
图 3.2.19

【试题3.2.16】 T形梁受压翼缘计算宽度（2009年）

某办公楼现浇钢筋混凝土三跨连续梁，其结构安全等级为二级，混凝土强度等级为C30，纵向钢筋采用HRB335级钢筋（），箍筋采用HPB235级钢筋（）。该梁的截面如图3.2.19所示。截面尺寸b×h=300mm×600mm，翼缘高度（楼板厚度）h_f′=100mm，楼面梁间净距S_n=3000mm。试问，当进行正截面受弯承载力计算时，该梁跨中截面受压区的翼缘计算宽度b_f′（mm）取下列何项数值最为合适？

（A）900 （B）1500

（C）2400 （D）3300

2.《混凝土结构设计规范》规定和算例

《混凝土结构设计规范》规定：

5.2.4 对现浇楼盖和装配整体式楼盖，宜考虑楼板作为翼缘对梁刚度和承载力的影响。梁受压区有效翼缘计算宽b_f′可按表5.2.4所列情况的最小值取用；也可采用梁刚度增大系数法近似考虑，刚度增大系数应根据梁有效翼缘尺寸与梁截面尺寸的相对比例确定。

表5.2.4 受弯构件受压区有效翼缘计算宽度b_f′

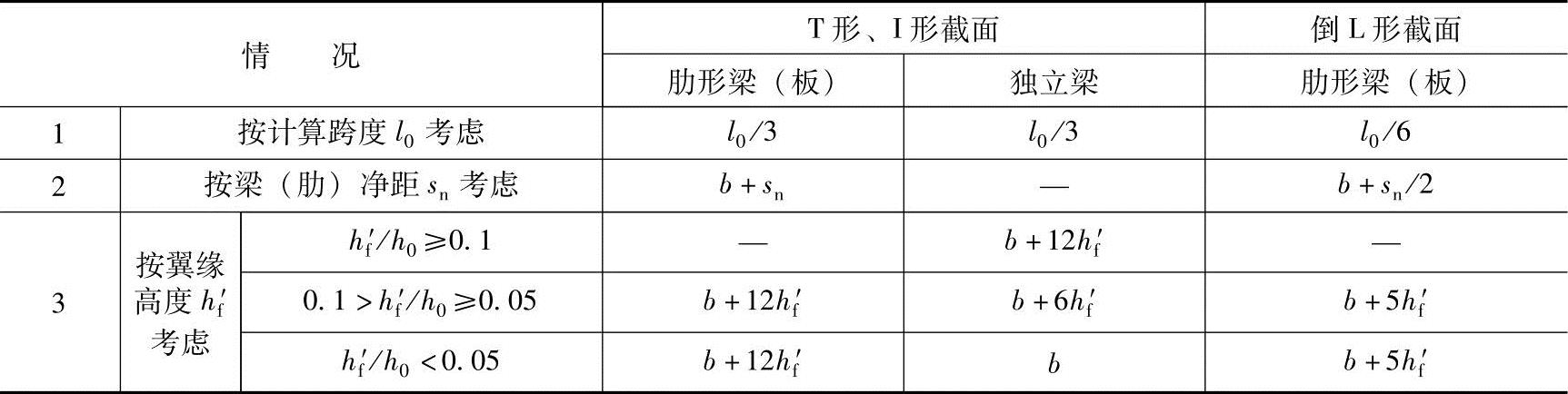
注：1.表中b为梁的腹板厚度；

2.肋形梁在梁跨内设有间距小于纵肋间距的横肋时，可不考虑表中情况3的规定；

3.加腋的T形、I形和倒L形截面，当受压区加腋的高度h_h不小于h_f′且加腋的长度b_h不大于3h_h时，其翼缘计算宽度可按表中情况3的规定分别增加2b_h（T形、I形截面）和b_h（倒L形截面）；

4.独立梁受压区的翼缘板在荷载作用下经验算沿纵肋方向可能产生裂缝时，其计算宽度应取腹板宽度b。

【例3.2.10】 T形梁的受压翼缘计算宽度

本题的条件和要求与【试题3.2.15】相同。

答案：（B）

由《混规》表5.2.4知：

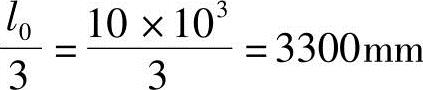
b_f′=b+s_n=200+1800=2000mm

b_f′/h₀=60/690=0.067>0.05

b_f′=b+12h_f′=200+12×60=920mm

取最小值b_f′=920mm。

【例3.2.11】 受压翼缘的计算宽度

某钢筋混凝土现浇肋形楼盖的次梁，如图3.2.20所示，次梁高度h=450mm，宽度b=200mm，次梁的计算跨度l₀=6m，间距为2.4m，净距s_n=2.2m，楼板厚度h_f′=80mm。

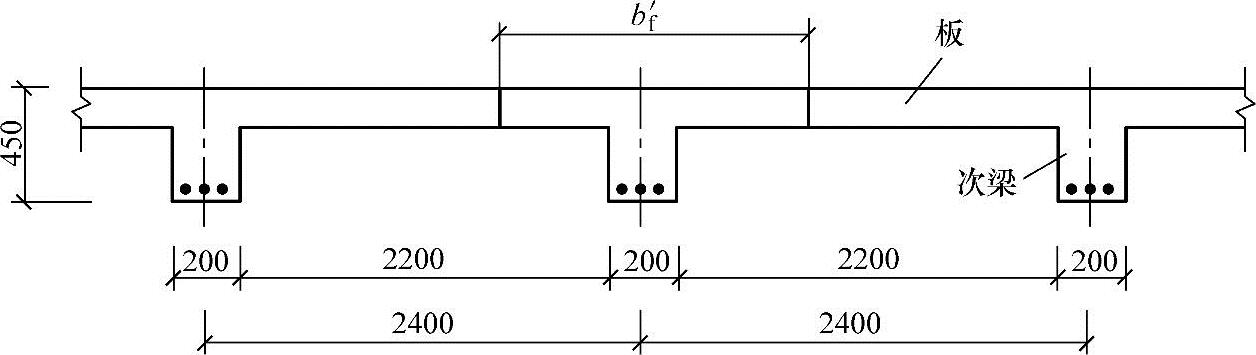
图 3.2.20

试问，翼缘的计算宽度b_f′（mm）最接近何项数值？

（A）2000 （B）2400 （C）1800 （D）2200

答案：（A）

按梁跨度l₀考虑：b_f′=l₀/3=2000mm

按梁净距考虑：b_f′=b+s_n=200+2200=2400mm

按翼缘高度考虑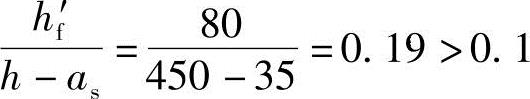：，对肋形梁不受此条件限制。

因此翼缘计算宽度b_f′=2000mm。

（二）T形、I形受弯构件

1.考试要求

（1）《考试大纲》规定：掌握

（2）“试题”回顾

【试题3.2.17】 单筋T形梁的纵向受拉钢筋截面面积（2002年）

有一根钢筋混凝土连续梁，结构安全等级为二级，混凝土强度等级为C30，纵向钢筋为Ⅲ级钢，假设梁的跨中截面按图3.2.21所示的T形截面考虑，在弯矩设计值M=200kN·m作用下，此单筋T形梁的纵向受拉钢筋截面面积（mm²）应和下列何项数值最为接近？

（A）1254 （B）1457

（C）1800 （D）1380

【试题3.2.18】 单筋T形梁的承载力计算（2005年）

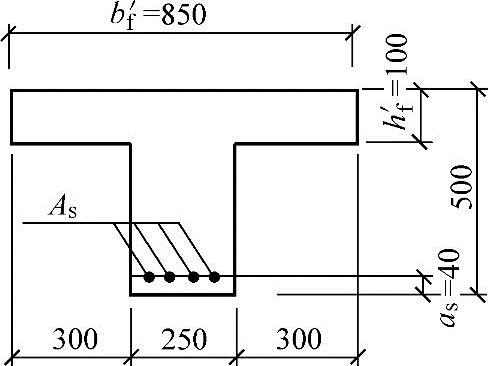
图 3.2.21

某钢筋混凝土T形截面简支梁，安全等级为二级，混凝土强度等级为C25，荷载简图及截面尺寸如图3.2.22所示。梁上均布静荷载g_k，均布活荷载g_q，集中静荷载G_k，集中活荷载P_k；各荷载均为标准值。已知：a_s=65mm，f_c=11.9N/mm²，f_y=360N/mm²。梁纵向受拉钢筋采用HRB400级且不配置受压钢筋时，该梁承受的最大弯矩设计值（kN·m）与下列何项最为接近？

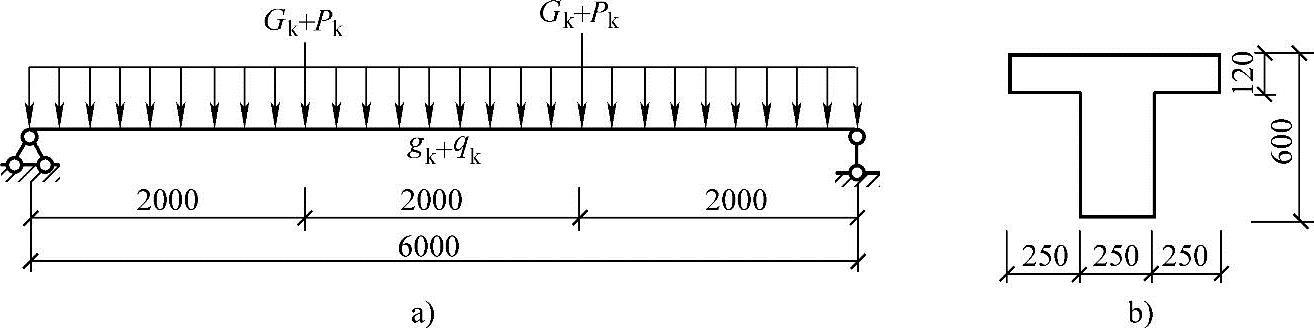
图 3.2.22

a）荷载简图 b）梁截面尺寸

（A）450 （B）523 （C）666 （D）688

【试题3.2.19】 槽形板的承载力计算（2008年）

某厂房楼盖预制钢筋混凝土槽形板的截面及配筋如图3.2.23所示，混凝土强度等级为C30，肋底部配置的HRB335级纵向受力钢筋为218（A_s=509mm²）。试问，当不考虑受压区纵向钢筋的作用时，该槽形板的跨中正截面受弯承载力设计值[M]（kN·m）与以下何项数值最为接近？

提示：a_s=30mm，a_s′=20mm。

（A）35 （B）40 （C）56 （D）72

【试题3.2.20】 箱形梁的承载力计算（2009年）

某承受竖向力作用的钢筋混凝土箱形截面梁，截面尺寸如图3.2.24所示；作用在梁上的荷载为均布荷载；混凝土强度等级为C25（f_c=11.9N/mm²，f_t=1.27N/mm²），纵向钢筋HRB335级，a_s=a_s′=35mm，已知该梁下部纵向钢筋配置为620。试问，该梁跨中正截面受弯承载力设计值M（kN·m）与下列哪个值最为接近？

提示：不考虑侧面纵向钢筋及上部受压钢筋的作用

（A）365 （B）410

（C）425 （D）480

【试题3.2.21】 双筋T形梁的承载力计算（2009年）

某办公楼现浇钢筋混凝土三跨连续梁如图3.2.25所示，其结构安全等级为二级，混凝土强度等级为C30，纵向钢筋采用HRB335级钢筋（），箍筋采用HPB235级钢筋（）。该梁AB跨跨中纵向受拉钢筋为425（A_s=1964mm²），跨中纵向受压钢筋为222（A_s′=760mm²），截面尺寸如图3.2.25所示，b_f′=900mm，a_s=a_s′=40mm。试问，该T形梁跨中截面受弯承载力设计值M（kN·m）与以下何项数值最为接近？

（A）289 （B）306

（C）317 （D）368

【试题3.2.22】 I形梁的承载力计算（2012年二级）

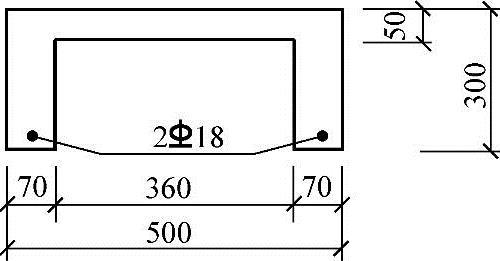
图 3.2.23

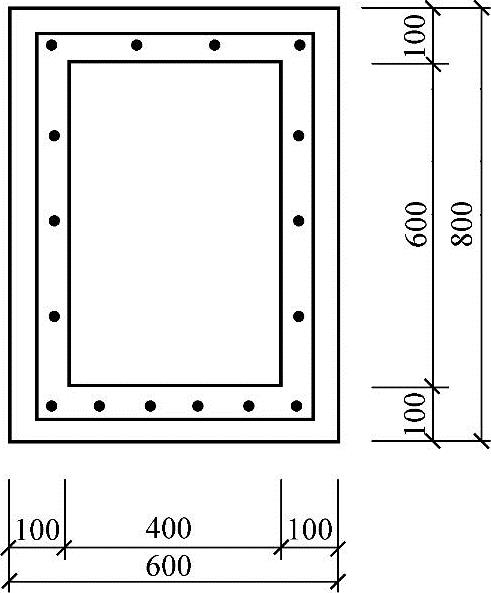
图 3.2.24

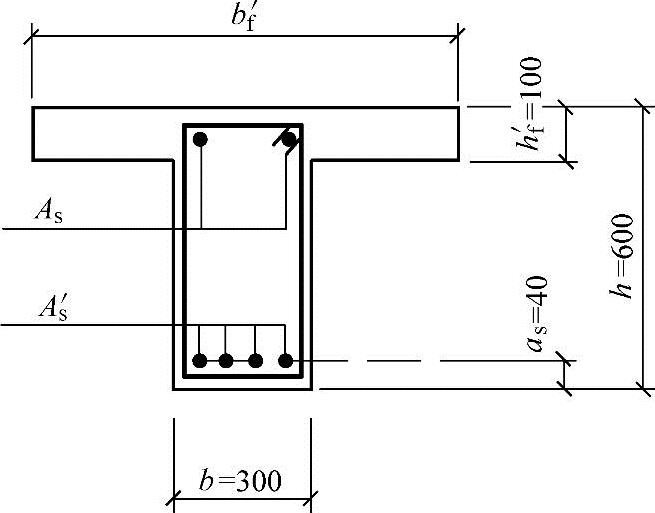
图 3.2.25

某钢筋混凝土简支梁，其截面可以简化成工字形如图3.2.26所示，混凝土强度等级为C30，纵向钢筋采用HRB400，纵向钢筋的保护层厚度为28mm，受拉钢筋合力点至梁截面受拉边缘的距离为40mm。该梁不承受地震作用，不直接承受重复荷载，安全等级为二级。

若该梁承受的弯矩设计值为310kN·m，并按单筋梁进行配筋计算。试问，按承载力要求该梁纵向受拉钢筋选择下列何项最为安全经济？

提示：不必验算最小配筋率。

（A）414+320 （B）414+322

（C）414+325 （D）414+328

2.《混凝土结构设计规范》的规定和算例

（1）《混凝土结构设计规范》的规定

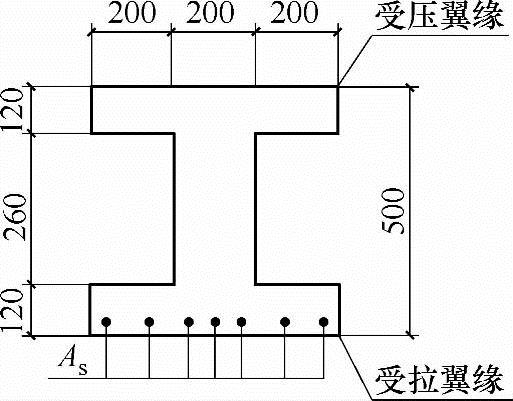
图 3.2.26

6.2.11 翼缘位于受压区的T形、I形截面受弯构件（图6.2.11），其正截面受弯承载力计算应符合下列规定：

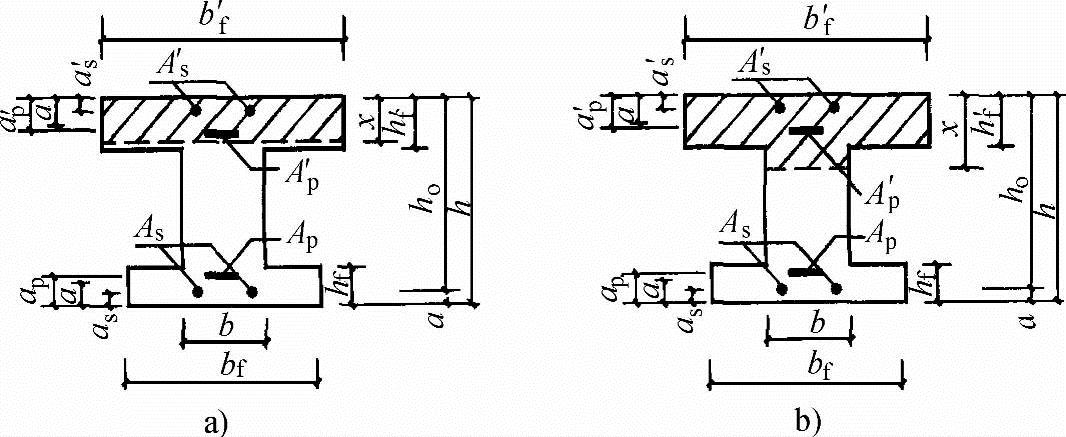
图6.2.11 I形截面受弯构件受压区高度位置

a）x≤h_f′ b）x>h_f′

1.当满足下列条件时，应按宽度为b_f′的矩形截面计算：

f_yA_s+f_pyA_p≤α₁f_cb_f′h_f′+f_y′A_s′-（σ_p′₀-f_py′）A_p′ （6.2.11-1）

2.当不满足公式（6.2.11-1）的条件时，应按下列公式计算：

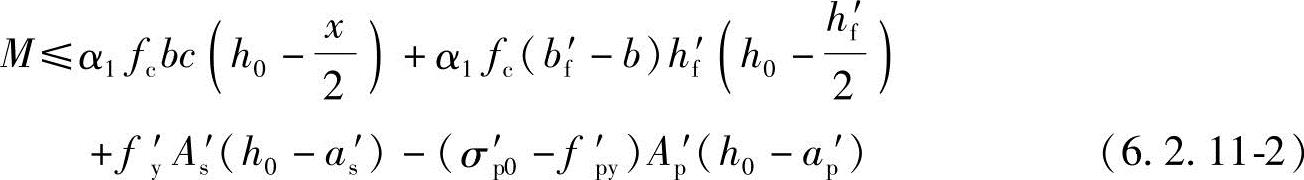
混凝土受压区高度应按下列公式确定：

α₁f_c[bx+（b_f′-b）h_f′]=f_yA_s-f_y′A_s′+f_pyA_p+（σ_p0′-f_py′）A_p′ （6.2.11-3）

式中 h_f′——T形、I形截面受压区的翼缘高度；

b_f′——T形、I形截面受压区的翼缘计算宽度，按本规范第6.2.12条的规定确定。

按上述公式计算T形、I形截面受弯构件时，混凝土受压区高度仍应符合本规范式（6.2.10-3）和式（6.2.10-4）的要求。

6.2.12 T形、I形及倒L形截面受弯构件位于受压区的翼缘计算宽度b_f′可按本规范表5.2.4所列情况中的最小值取用。

（2）计算类型的判定

为判定T形截面属于何种类型，可把x=h_f′作为界限情况进行受力分析，由平衡条件可得

∑x=0 α₁f_cb_f′h_f′=A_sf_y （3.2.1）

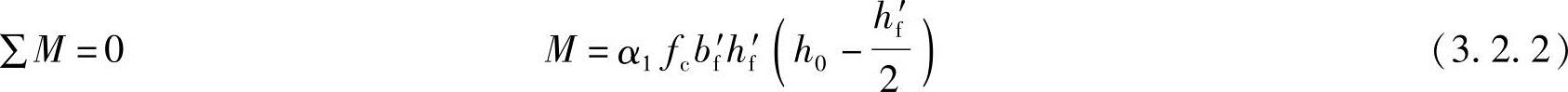
进行钢筋面积计算时，由于弯矩设计值M已知，可用式（3.2.2）来判定。若 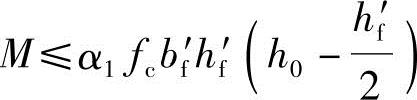（第一类T形）若 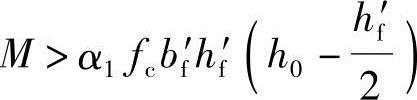（第二类T形）

进行承载力校核时，由于钢筋截面积A_s已知，可用式（3.2.1）来判定。

若f_yA_s≤α₁f_cb_f′h_f′ （第一类T形）

若f_yA_s>α₁f_cb_f′h_f′ （第二类T形）

【例3.2.12】 计算类型确定

条件：已知预制空心楼板如图3.2.27所示。混凝土C30，f_c=14.3N/mm²，f_t=1.43N/mm²，受拉钢筋为98（A_s=453mm²），f_y=270N/mm²，h₀=105mm。环境类别一类。

要求：判别T形截面的类型。

解答：

（1）查《混规》表8.2.1知，一类环境，C30混凝土的保护层c=15mm，设a_s=20mm。

（2）圆孔空心板换算为工字形截面

换算条件是保持截面面积不变，保持截面惯性矩不变。设圆孔直径为d，换算的矩形孔宽b_h，高h_h。则：，。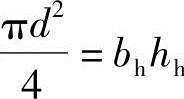

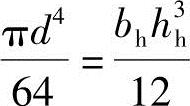解得：h_h=0.866d=0.866×80=69.2mm，b_h=0.907d=0.907×80=72.6mm，∑b_h=72.6×8=580.8mm，则腹板宽：b=（850+890）/2-580.8=289.2mm≈290mm。

换算的工形截面如图3.2.26b所示。b=290mm，h=125mm，b_f′=850mm，h_f′=30.4mm，b_f=890mm，h_f=25.4mm。

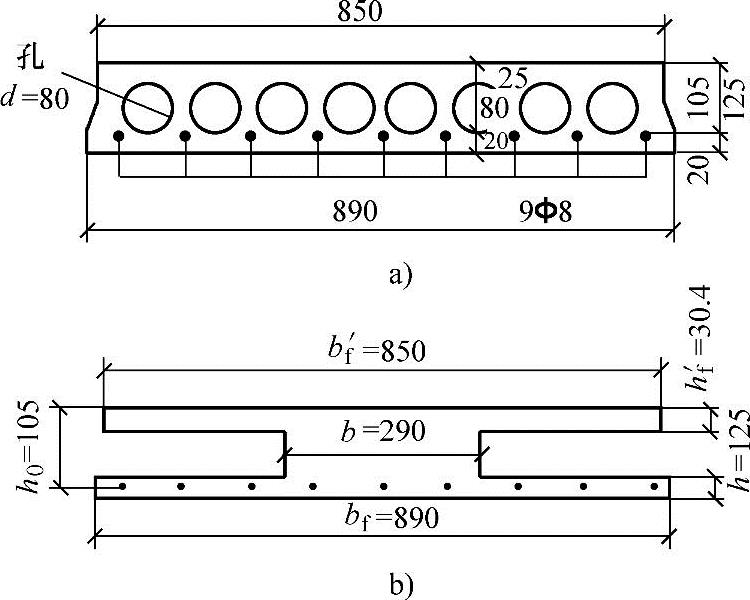
图3.2.27 空心板截面和配筋

a）空心板截面 b）换算的工形截面

（3）判别T形截面类型

由《混规》式（6.2.11-1）判断截面类型：

f_yA_s=270×453=122.31kN<α₁f_cb_f′h_f′=14.3×850×30.4=369.5kN，为第一类T形截面。

（3）承载力计算

已知截面尺寸b、h及b_f′、h_f′，材料强度f_c、f_y及配置钢筋截面面积A_s。计算截面的承载能力M_u。

1）根据《混凝土结构设计规范》式（6.2.11-1）判别T形截面梁的类型

当f_yA_s≤α₁f_cb_f′h_f′时，属第一类T形，可按b_f′×h的单筋矩形截面梁计算。

由《混凝土结构设计规范》式（6.2.10-2）计算x，

由《混凝土结构设计规范》式（6.2.10-1）计算M。

若f_yA_s>α₁f_cb_f′h_f′时，属第二类T形，则进入下一步。

2）求出x及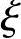，由《混凝土结构设计规范》式（6.2.11-3）得到

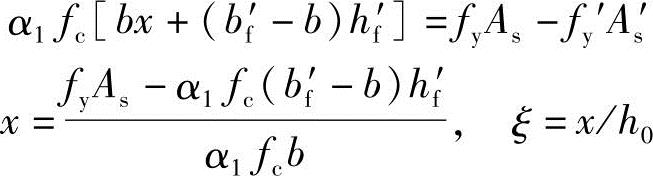
3）根据《混凝土结构设计规范》式（6.2.10-3）验算压区高度x，此时，x可能出现如下二种情况：

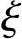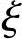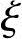若≤_b或x≤_bh₀，则转入4）中①；

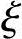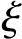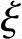若>_b或x>_bh₀，则转入4）中②。

4）确定受弯承载力M_u

①根据《混凝土结构设计规范》式（6.2.11-2）求出受弯承载力M_u。

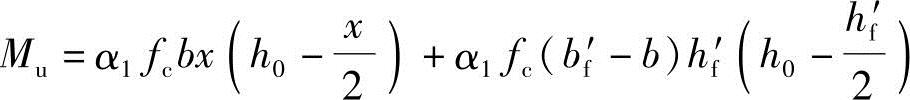
②根据《混凝土结构设计规范》式（6.2.11-5）求受弯承载力M_u。

取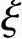=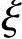_b或x=_bh₀得到

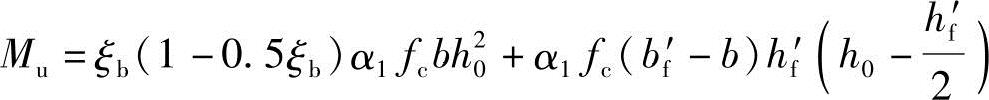
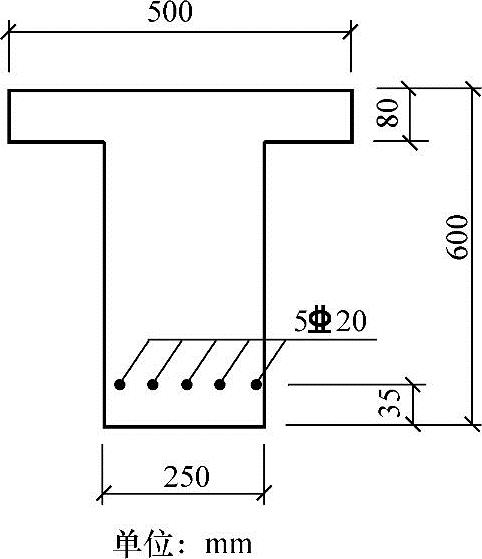
图3.2.28 T形梁截面配筋图

【例3.2.13】 第一类T形截面梁的受弯承载力计算

条件：已知某工程T形截面独立梁，如图3.2.28所示，b_f′=500mm，b=250mm，h_f′=80mm，h=600mm，混凝土强度等级为C30（f_c=14.3N/mm²，f_t=1.43N/mm²，α₁=1.0，β₁=0.8，ε_cu=0.0033），钢筋为HRB400级（f_y=360N/mm²），E_s=2.0×10⁵ N/mm²，_b=0.518），纵向受拉钢筋520（A_s=1571mm²）。安全等级二级，环境类别为一类。

要求：确定该梁截面的极限弯矩设计值M_u。

解答：根据《混规》表8.2.1查得保护层厚度c=20mm，取a_s=35mm。

（1）根据《混规》式（6.2.11-1）f_yA_s≤α₁f_cb_f′h_f′，判断T形截面的类型，将已知条件代入可得：

α₁f_cb_f′h_f′=1.0×14.3×500×80=572000N·mm>f_yA_s=360×1571=565560N·mm

属于第一类T形截面，故按截面宽度为b_f′=500mm的矩形截面进行计算。

按b×h=500mm×600mm的单筋矩形截面梁计算。

（2）验算最小配筋率（可略去）

（3）求压区高度x

由《混规》式（6.2.10-2）：

α₁f_cbx=f_yA_s

代入已知条件可得：

1.0×14.3×500x=360×1571

得x=79mm

（4）验算压区高度x是否满足《混规》式（6.2.10-3）（可略去）

（5）确定受弯承载力

根据《混凝土结构设计规范》式（6.2.10-1）知

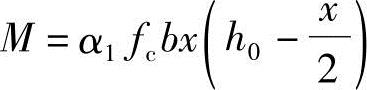
代入已知条件

M_u=1.0×14.3×500x（565-0.5x）

=1.0×14.3×500×79×（565-0.5×79）

=296828675N·mm

≈296.8kN·m

【例3.2.14】 槽形板的受弯承载力计算

条件：某多层厂房楼盖预制槽形板如图3.2.29所示。f_c=14.3N/mm²，纵筋为216（A_s=402mm²），f_y=300N/mm²，f_t=1.43N/mm²，h₀=270mm。

要求：计算槽形板的受弯承载力。

解答：（1）根据《混规》式（6.2.11-1）f_yA_s≤α₁f_cb_f′h_f′，判别截面类型

将已知条件代入可得

f_yA_s=300×402=120.6kN

α₁f_cb_f′h_f′=14.3×500×50=357.5kN

f_yA_s<α₁f_cb_f′h_f′

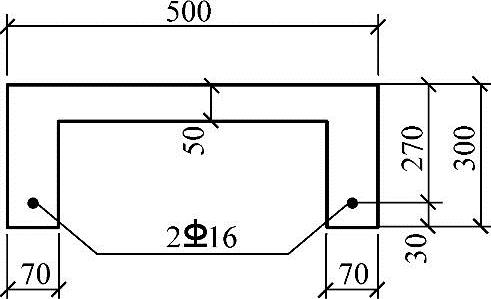
图3.2.29 槽形板截面配筋图

故为第一类T形截面。可按b_f′×h=500mm×300mm单筋矩形截面梁计算，下面按单筋梁步骤计算。

（2）根据《混规》第8.5.1条规定的最小配筋率的要求

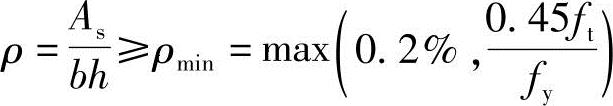
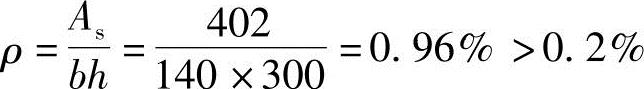，且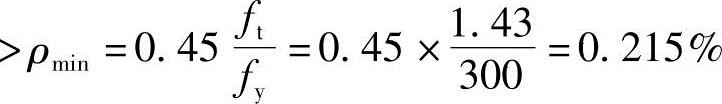，满足要求。

（3）求压区高度x

由《混规》式（6.2.10-2）α₁f_cbx=f_yA_s，可得

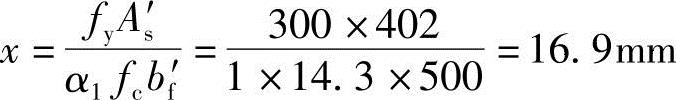
（4）验算压区高度x

由《混规》式（6.2.10-3），x≤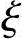_bh₀，可得x=16.9mm≤0.55×270mm=148mm

（5）求受弯承载力M由《混规》式（6.2.10-1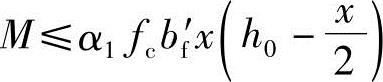）：代入已知条件

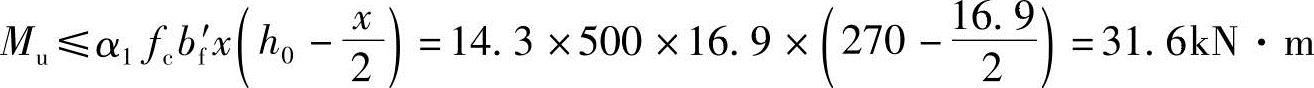
【例3.2.15】 第二类T形截面梁的受弯承载力计算

条件：已知T形截面梁如图3.2.30所示。h₀=740mm，f_c=9.6N/mm²，纵筋为820（A_s=2513mm²），f_y=360N/mm²，_b=0.518。

要求：计算该T形截面梁的受弯承载力。

解答：

（1）判别类型

应用《混规》式（6.2-11）f_yA_s=α₁f_cb_f′h_f′，判别截面类型。代入已知条件

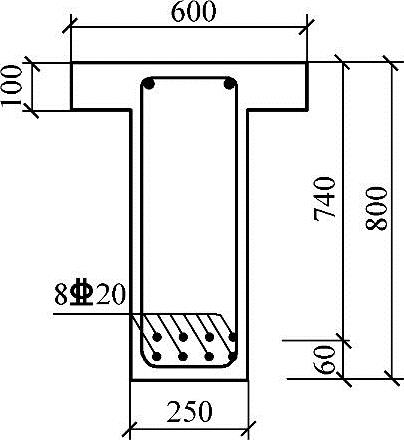
图3.2.30 T形梁截面配筋图

f_yA_s=360×2513=904.7kN>α₁f_cb_f′h_f′

=9.6×600×100=576kN

故为第二类T形截面。

（2）求压区高度x

由《混规》式（6.2.11-3）：

α₁f_c[bx+（b_f′-b）h_f′]=f_yA_s-f_y′A_s′

代入已知条件

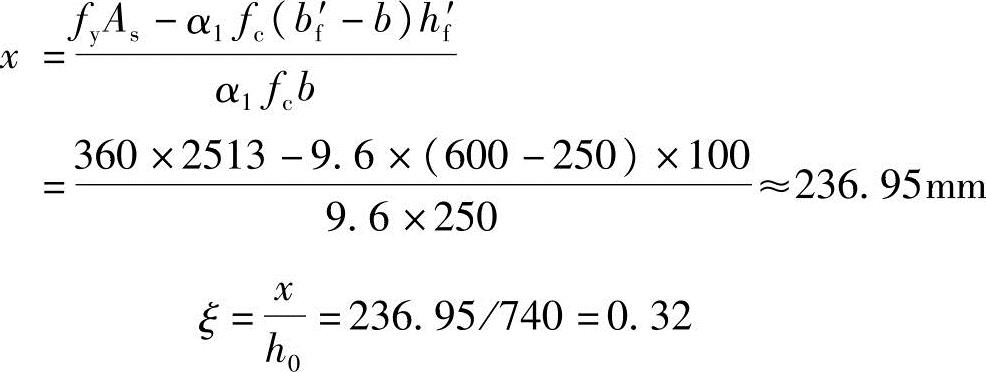
（3）验算压区高度x是否满足

由《混规》式（6.2.10-3）：

x=236.95<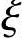_bh₀=0.518×740=383.32mm

或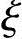=0.32<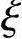_b=0.518，满足要求。

（4）确定受弯承载力M

由《混规》式（6.2.11-2）：

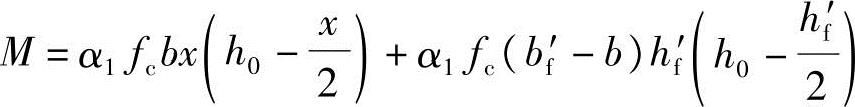
代入已知条件可得

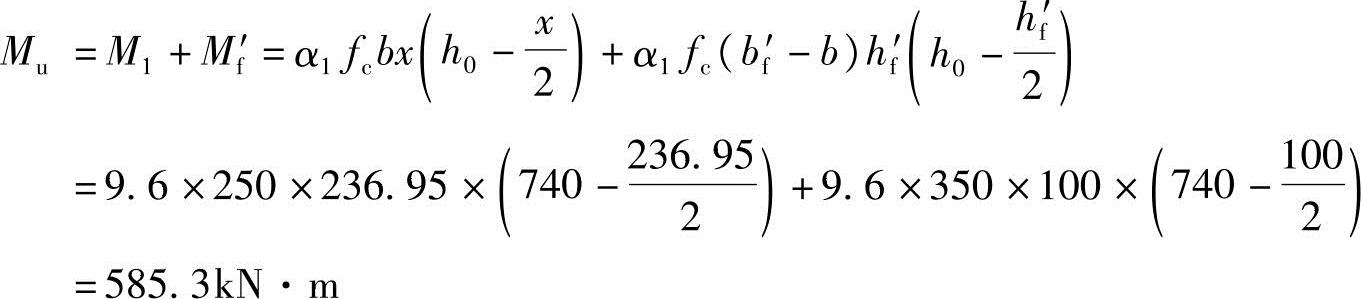
（4）配筋计算

已知截面尺寸b、h、b_f′、h_f′，材料强度f_c、f_y及弯矩设计值M。

计算所需钢筋截面面积A_s。

1）判定截面类型

若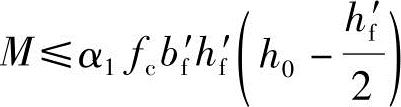时，属第一类型，可按b_f′×h的矩形截面计算。

若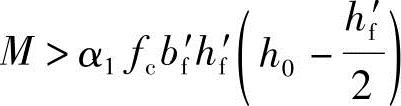时，属第二类型，则进入下一步。

2）求压区高度x，由《混凝土结构设计规范》式（6.2.11-2），得

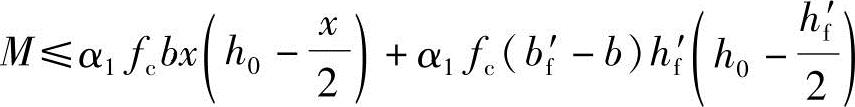
得到

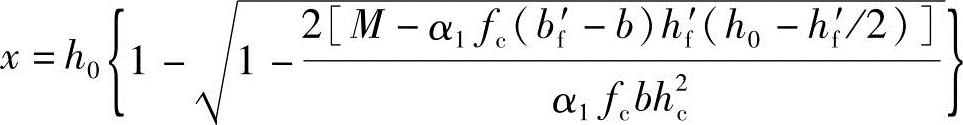
3）根据《混凝土结构设计规范》式（6.2.10-3）验算压区高度x，此时，x可能出现如下二种情况：

若x>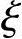_bh₀，为超筋梁；

若2a_s′≤x≤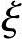_bh₀，则进入下一步。

4）求受拉钢筋A_s，由《混凝土结构设计规范》式（6.2.11-3）知

α₁f_c[bx+（b_f′-b）h_f′]=f_yA_s-f_y′A_s′

得到

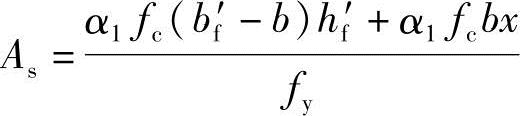
【例3.2.16】 第一类T形截面独立梁的配筋计算

条件：已知一肋形楼盖的次梁，弯矩设计值M=410kN·m，梁的截面尺寸为b×h=200mm×600mm，b_f′=1000mm，h_f′=90mm；混凝土等级为C25，钢筋采用HRB400级，环境类别为一类。

要求：求受拉钢筋截面面积A_s。

解答：查《混规》表8.2.1得保护层厚度c=25mm，当钢筋排成两排时，设a_s=65mm。根据《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条得f_c=11.9N/mm²，f_y=f_y′=360N/mm²，α₁=1.0，β₁=0.8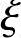，_b=0.518

（1）判别类型

根据《混规》式（6.2.11-2）知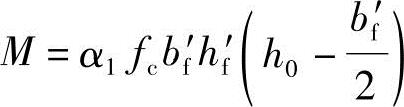，代入已知条件。因弯矩较大，截面宽度b较窄，预计受拉钢筋需排成两排，故取

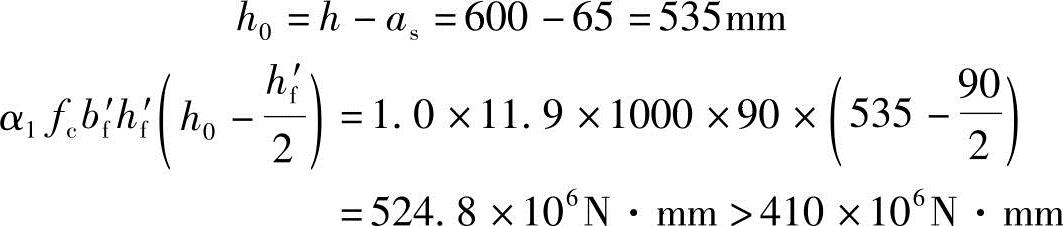
属于第一种类型的T形梁，以b_f′代替b。按b_f′×h=1000mm×600mm矩形梁计算。

（2）求压区高度x

由《混规》式（6.2.10-1）知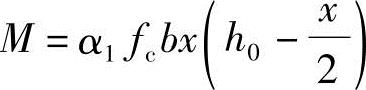得

（3）验算压区高度x

由《混规》式（6.2.10-3）x≤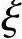_bh₀，可得(www.xing528.com)

x=68.8mm<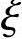_bh₀=0.518×535=277.1mm

（4）求受拉钢筋面积A_s

由《混规》式（6.2.10-2）α₁f_cbx=f_yA_s，可得

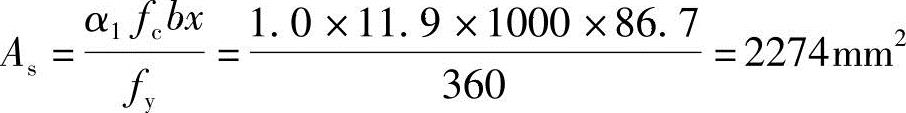
选用622，A_s=2281mm²。

【例3.2.17】 第二类T形截面独立梁的配筋计算

条件：已知弯矩M=650kN·m，混凝土等级为C30，钢筋采用HRB400级，梁的截面尺寸为b×h=300mm×700mm，b_f′=600mm，h_f′=120mm；环境类别为一类。

要求：求所需的受拉钢筋截面面积A_s。

解答：根据《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条，得f_c=14.3N/mm²，f_y=f_y′=360N/mm²，α₁=1.0，β₁=0.8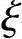，_b=0.518。

（1）判别截面类型

根据《混规》式（6.2.11-2）知

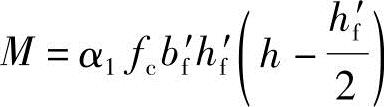
假设受拉钢筋排成两排，故取h₀=h-a_s=700-60=640mm代入已知条件可得

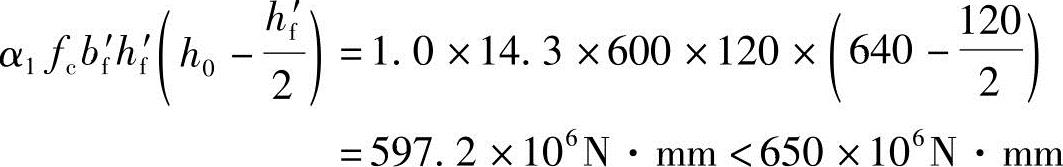
属于第二类型的T形截面。

（2）求压区高度x

由《混规》式（6.2.11-2）知

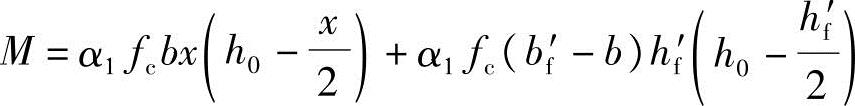
得到

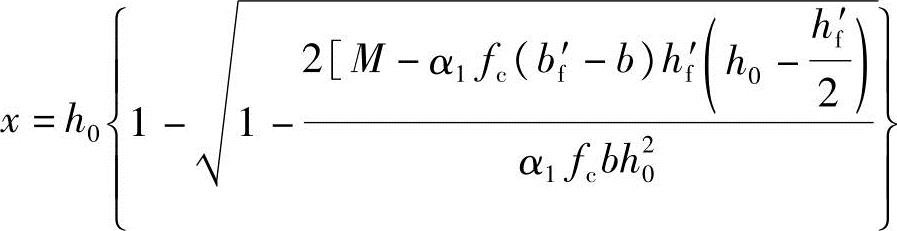
代入已知条件，得

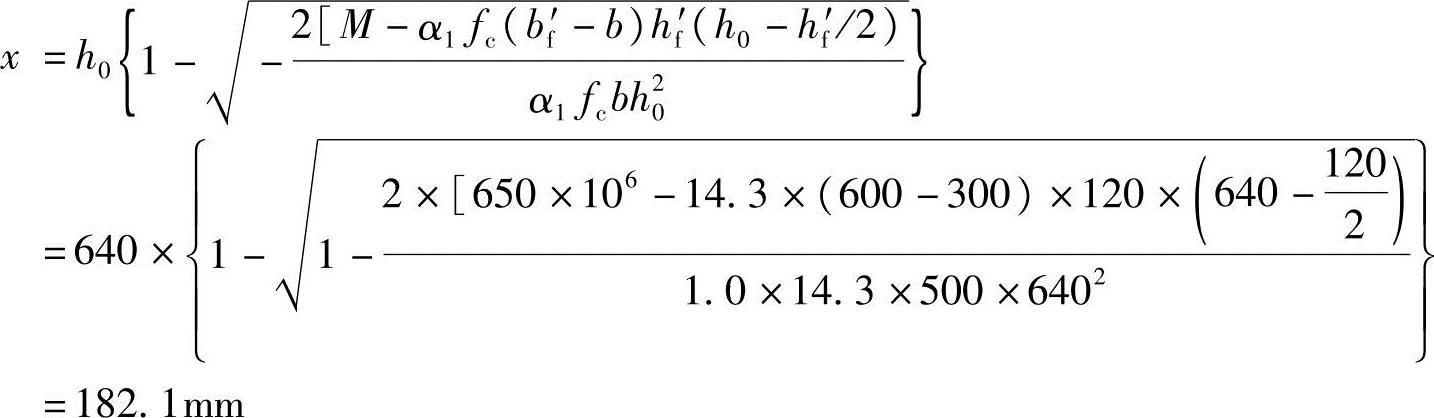
（3）验算压区高度x

由《混规》式（6.2.10-3），x≤_bh₀

x=182.1mm<_bh₀=0.518×640=331.52mm

（4）求受拉钢筋A_s

由《混规》式（6.2.11-3）知

α₁f_c[bx+（b_f′-b）h_f′]=f_yA_s-f_y′A_s′

可得

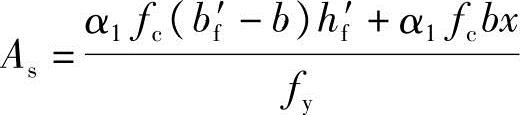
将已知条件代入

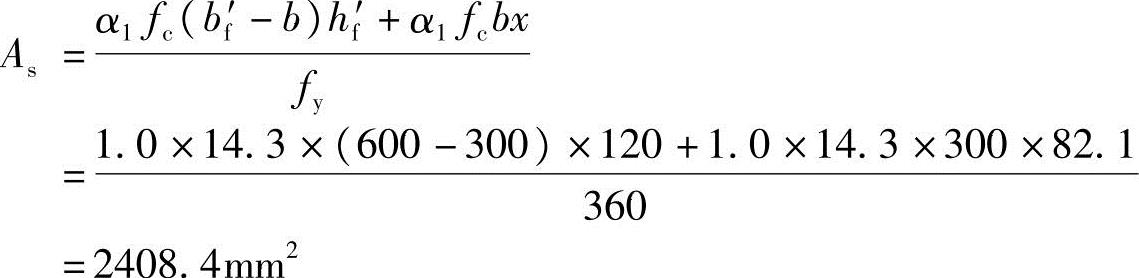
选配820，A_s=2513mm²。

【例3.2.18】 肋形楼盖次梁的配筋计算

条件：某肋形楼盖的次梁，跨度为6m，间距为2.4m，截面尺寸如图3.2.31所示。跨中最大正弯矩M=80.8kN·m。混凝土强度等级C25（f_c=9.6N/mm²），f_t=1.10N/mm²，α₁=1.0），钢筋为HRB400级（f_y=360N/mm²），安全等级二级，环境类别为一类。

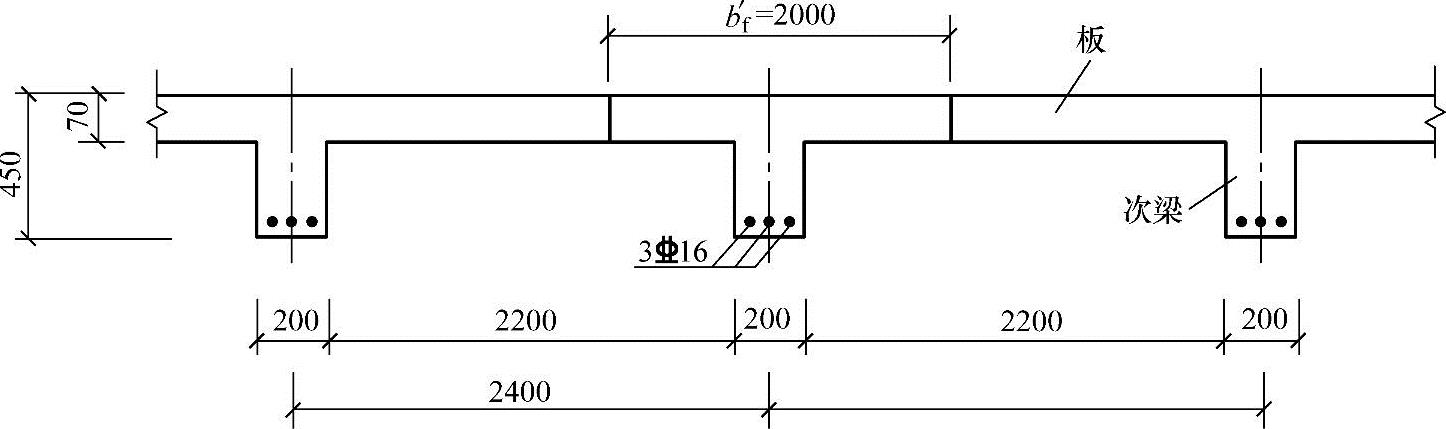
图3.2.31 次梁的截面配筋图

要求：计算该次梁受拉钢筋面积A_s。

解答：（1）由《混规》表8.2.1查得C20的保护层厚度c=25mm，设a_s=40mm，_b=0.518。

（2）确定翼缘计算宽度b_f′

根据《混规》表5.2.4可得：

按梁跨度l考虑：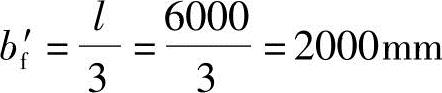

按梁净距考虑：b_f′=b+s_n=200+2200=2400mm

按翼缘厚度h_f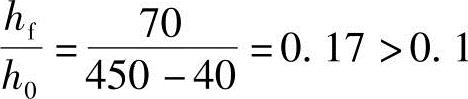′考虑：，不考虑。

最后，翼缘宽度取前两项计算结果中的较小值，即

b_f′=2000mm

（3）判别T形截面类型

由《混规》式（6.2.11-2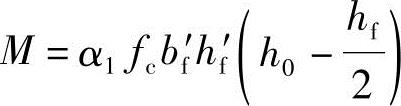），，代入已知条件得

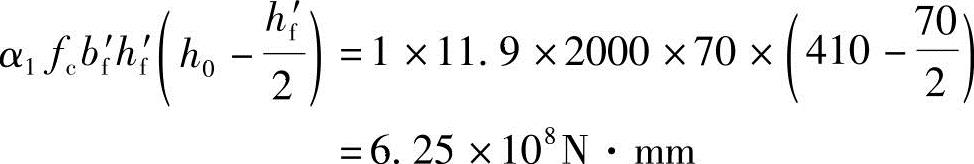
=625kN·m>80.8kN·m

故属于第一类T形截面。可按b_f′×h=2000mm×450mm的矩形梁计算。

（4）求压区高度x

由《混规》式（6.2.10-1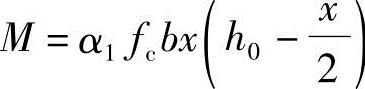），，可得

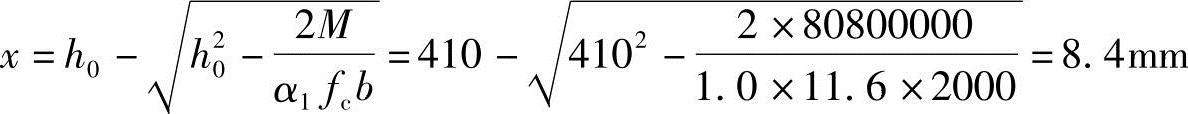
（5）验算压区高度x

由《混规》式（6.2.10-3），x≤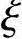_bh₀

x=8.4≤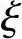_bh₀=0.518×410=212.4mm

（6）求受拉钢筋A_s

由《混规》式（6.2.10-2）α₁f_cbx=f_yA_s，可得

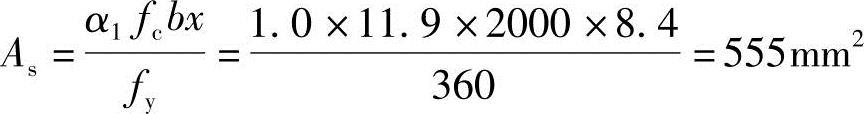
实选316（A_s=603mm²）。

（7）验算受拉钢筋的最小配筋率

最小配筋率按《混规》表8.5.1确定，即

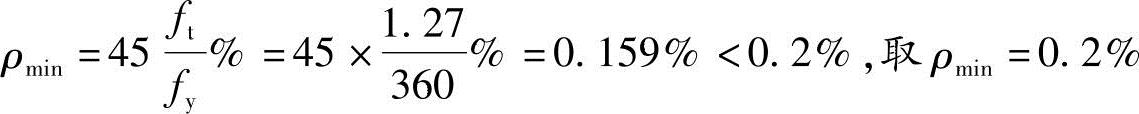
A_s，min=0.2%×200×450=180mm²，A_s=603mm²>A_s，min，满足要求。

（三）模拟考题

（1）计算类型确定

【3.2.13】～【3.2.14】 某预制的钢筋混凝土简支空心板，截面形状尺寸如图3.2.32所示。混凝土强度等级为C30。钢筋为HRB400，γ₀=1.0。跨中最大弯矩设计值M_d=3.6×10⁸N·mm，采用绑扎钢筋骨架，设一层受拉主筋，受拉边缘至钢筋重心的距离a_s=40mm。

【3.2.13】 将空心板的圆孔换算成等效的矩形孔，圆孔的直径为D，方孔的宽度和高度分别为b_k和h_k，等效矩形孔尺寸h_k（mm）和b_k（mm）最接近何项数值？

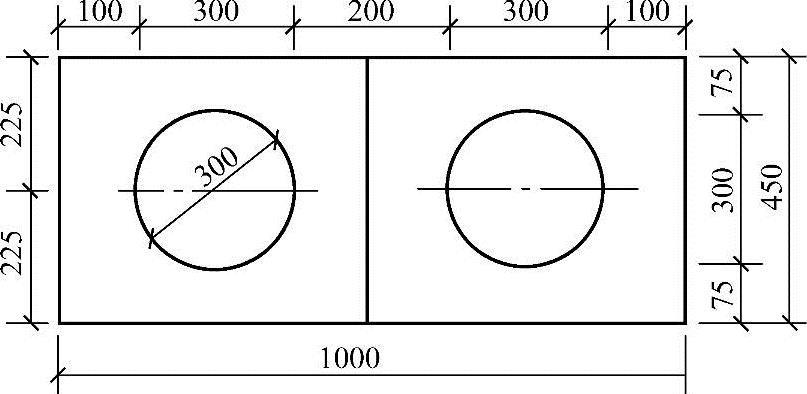
图 3.2.32

（A）259.8，272 （B）272，316 （C）259.8，316 （D）272，259.8

答案：（A）

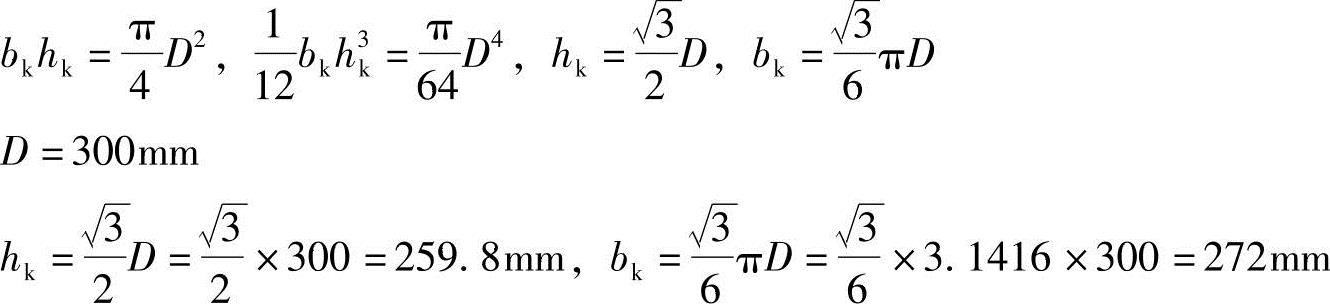
【3.2.14】 该截面的截面类型为何项？

（A）第一类 （B）第二类

答案：（A）

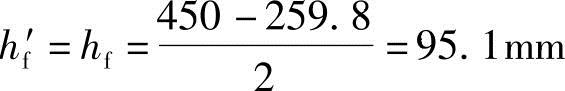
腹板的厚度为：b=1000-2×272=456mm换算后的截面如图3.2.33所示。

α₁f_cb_f′h_f′（h₀-h_f′/2）

=14.3×1000×95.1×（410-95.1/2）

=4.93×10⁸N·mm

>M_d=3.6×10⁸N·mm

属第一类T形截面。

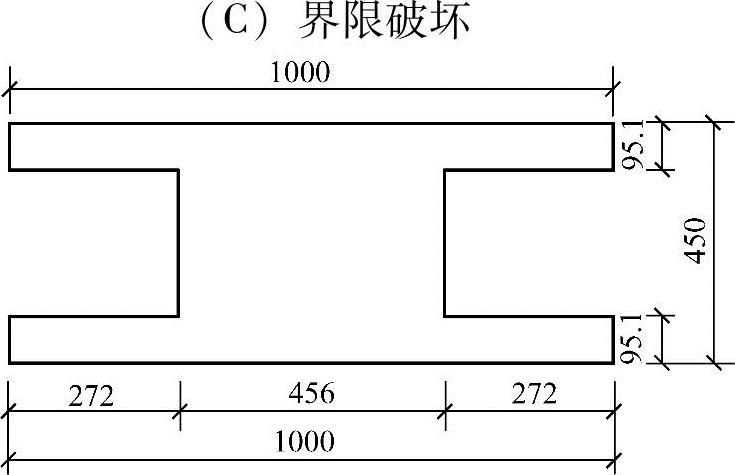
图 3.2.33

（2）承载力计算

【3.2.15】 T形截面梁（图3.2.34），b_f′=500mm，b=200mm，h_f′=80mm，a_s=40mm，混凝土等级为C25，纵向受拉钢筋为HRB400级，用420，A_s=1256mm²，求此梁所能承受的弯矩M_u（kN·m）为何项数值？

（A）211.68 （B）237.12

（C）236.8 （D）247.52

答案：（C）

Ⅰ.详细解答

据《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条查得f_c=11.9N/mm²，f_y=360N/mm²，α₁=1.0h₀=600-40=560mm，_b=0.518

（1）判别类型

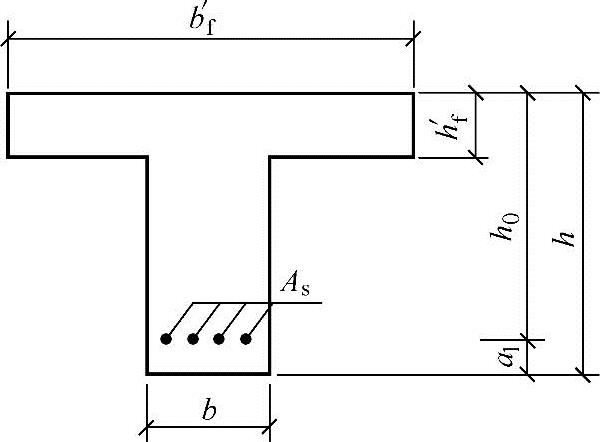
图 3.2.34

由《混规》式（6.2.11-1）f_yA_s=α₁f_cb_f′h_f′，求得

f_yA_s=360×1256=452160N

α₁f_cb_f′h_f′=1.0×11.9×500×80=476000N

f_yA_s<α₁f_cb_f′h_f′

为第一类T形截面梁，故计算按截面宽度为b_f′的矩形截面进行。

（2）求出压区高度x

由《混规》式（6.2.10-2）α₁f_cbx=f_yA_s，可得

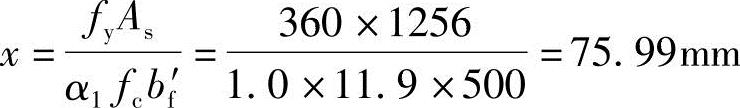
（3）验算压区高度x

根据《混规》式（6.2.10-3）x≤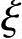_bh₀x=75.99mm≤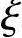_bh₀=0.518×560=209.1mm

（4）求受弯承载力M

由《混规》式（6.2.10-1）知

M=α₁f_cb_f′x（h₀-x/2）

M_u=1.0×11.9×500×75.99×（560-75.99/2）

=236.02×10⁶N·mm=236.02kN·m

Ⅱ.简要解答

（1）α₁f_cb_fh_f′=1.0×11.9×500×80=476000N>f_yA_s=360×1256=452160N；

（2）为第一类T形梁，可按b_f′×h=500mm×600mm的矩形截面梁计算；

【3.2.16】 已知一T形截面梁的截面尺寸h=700mm、b=250mm、h_f′=100mm、b_f′=600mm，截面配有HRB400级受拉钢筋822（A_s=3041mm²），混凝土强度等级C30，求梁截面的极限弯矩M_u（kN·m）。

（A）626 （B）634 （C）756 （D）542

答案：（A）

Ⅰ.详细解答

已知条件：根据《混规》第4.1.4条、4.2.3条、6.2.6条，6.2.7条，混凝土强度等级C30，α₁=1.0，f_c=14.3N/mm²；HRB400钢筋，f_y=360N/mm²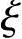，_b=0.518，a_s=60mm，h₀=700-60=640mm。

（1）判别截面类别

由《混规》式（6.2.11-1）得

f_yA_s=360×3041=1094760N>α₁f_cb_f′h_f′=14.3×600×100=85800N

属第二类T形截面。

（2）计算压区x

由《混规》式（6.2.11-3）得

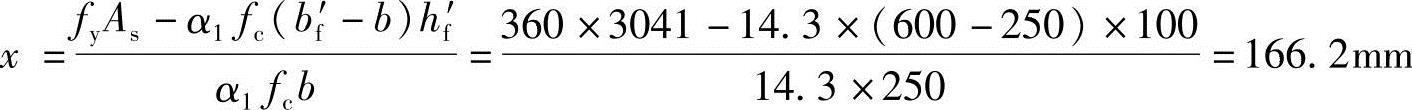
（3）验算压区高度x

根据《混规》式（6.2.10-3）得

x=166.2mm<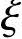_bh₀=0.518×640=331.5mm

（4）计算极限弯矩M_u

由《混规》式（6.2.11-2）得

M_u=α₁f_c（b_f′-b）h_f′（h₀-h_f′/2）+α₁f_cbx（h₀-x/2）

=14.3×（600-250）×100×（640-100/2）+14.3×250×166.2×（640-166.2/2）

=626185488N·mm=626.185kN·m

Ⅱ.简要解答

（1）f_yA_s=360×3041=1094760N>α₁f_cb_f′h_f′=1.0×14.3×600×100=85800N，属第二类T形梁；

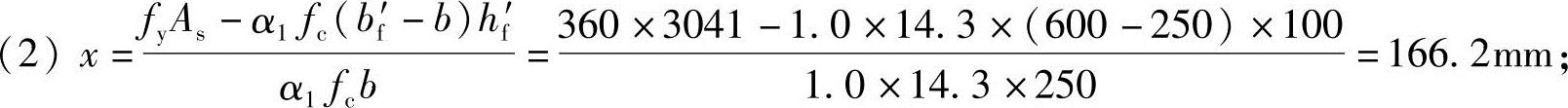
（3）x=166.2mm<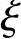_bh₀=0.518×640=331.5mm；

【3.2.17】～【3.2.18】 已知一个T形截面梁截面尺寸b_f′=600mm、h_f′=120mm、b=250mm、h=650mm，混凝土强度等级C25，采用HRB400钢筋，梁所承受的弯矩设计值M=552kN·m。已知属第二类T形截面。

查《混凝土结构设计规范》第4.1.4条、4.2.3条、6.2.6条、6.2.7条得f_c=11.9N/mm²，f_y=360N/mm²，α₁=1.0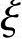，_b=0.518，a_s=60mm（两排），h₀=650-60=590mm。

【3.2.17】 受压区高度x（mm）最接近下列何项数值？

（A）196 （B）314 （C）210 （D）570

答案：（A）

由《混规》式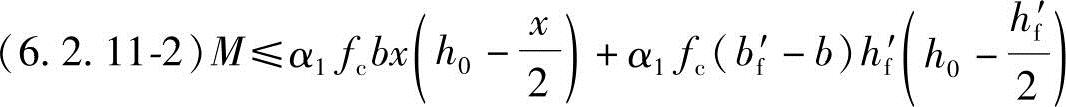，可得

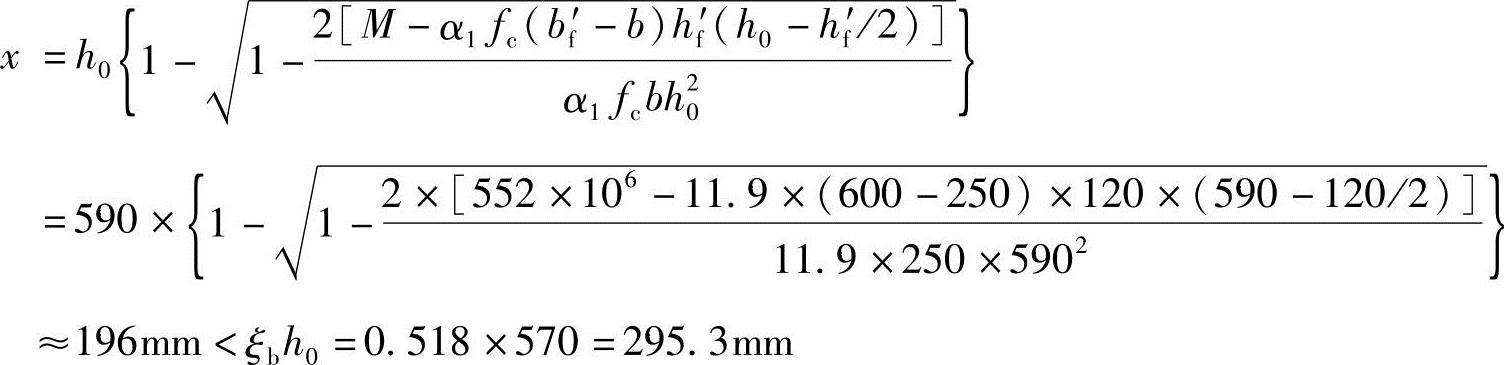
【3.2.18】 受拉钢筋面积A_s（mm²）最接近下列何项数值？

（A）3008 （B）1575 （C）2546 （D）1865

答案：（A）

由《混规》式（6.2.11-3），α₁f_c[bx+（b_f′-b）h_f′]=f_yA_s-f_y′A_s′，可得

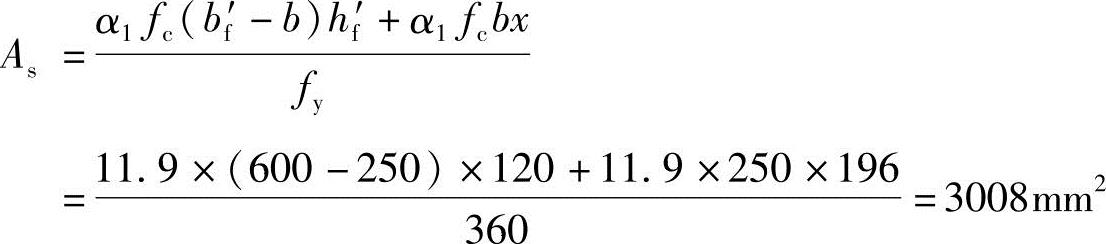
（3）配筋计算

【3.2.19】 单筋T形梁的承载力计算（2005年，因规范改版，本题已作相应调整）。

某钢筋混凝土T形截面简支梁，安全等级为二级，混凝土强度等级为C25，荷载简图及截面尺寸如图3.2.35所示。梁上均布静荷载g_k，均布活荷载g_q，集中静荷载G_k，集中活荷载P_k；各荷载均为标准值。已知：a_s=65mm，f_c=11.9N/mm²，f_y=360N/mm²。梁纵向受拉钢筋采用HRB400级且不配置受压钢筋时，该梁承受的最大弯矩设计值（kN·m）与下列何项最为接近？

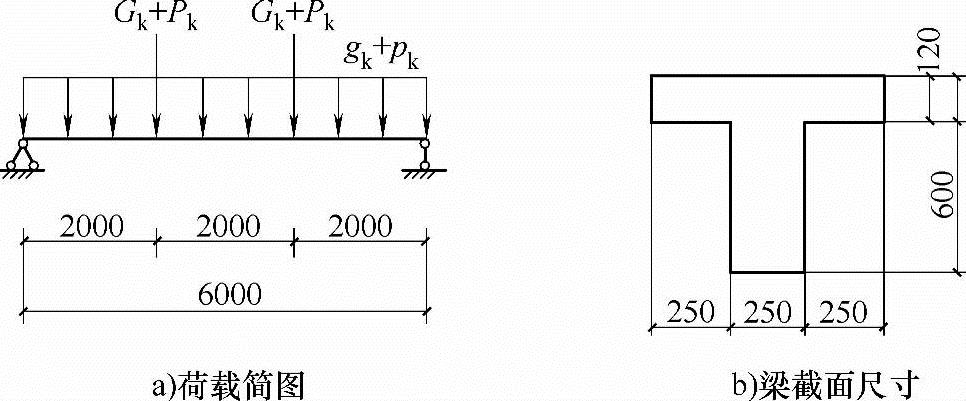
图 3.2.35

（A）450 （B）523 （C）666 （D）688

答案：（C）

（1）《混规》6.2.1-3条：

ε_cu=0.0033-（f_cu，k-50）×10^-5=0.0033-（25-50）×10^-5>0.0033，取ε_cu=0.0033

（2）《混规》6.2.7条，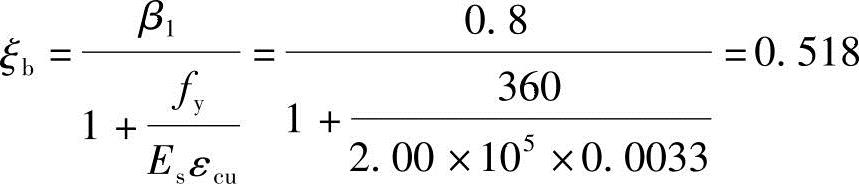

（3）x_b=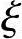_bh₀=0.518×（600-65）=277.13mm

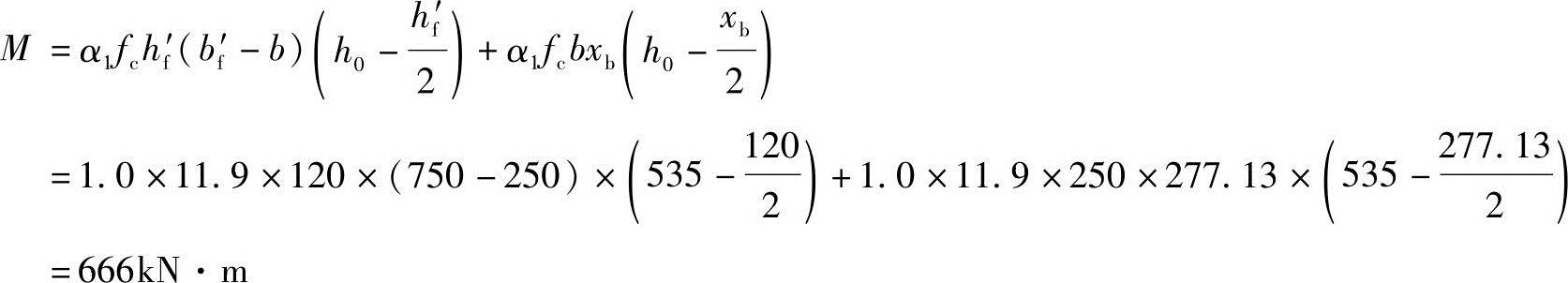
【3.2.20】 若已知翼缘计算宽度b_f′=1800mm，弯矩设计值M=115kN·m，按单筋T形截面计算的次梁跨中所需受拉钢筋计算截面面积（mm²）与下列何项数值最为接近？

（A）1009 （B）1033 （C）940 （D）1124

答案：（A）

Ⅰ.详细解答

已知条件：由《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条知：

混凝土强度：C30，f_c=14.3N/mm²，f_t=1.43N/mm²；

钢筋强度：f_y=360N/mm²，f_y′=360N/mm²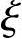，_b=0.518，a_s=35mm，h₀=450-35=415mm；

弯矩值：M=115kN·m。

（1）截面类型判别

由《混规》式（6.2.11-2）知

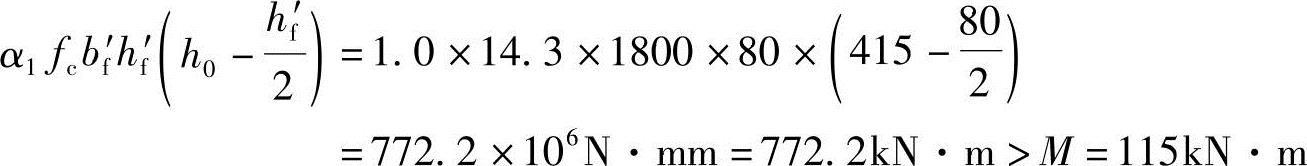
属于第一类T形截面，即可将截面按宽度为b_f′的矩形截面计算。

（2）计算压区高度x

由《混规》式（6.2.10.1），可以得到受压区高度x计算式：

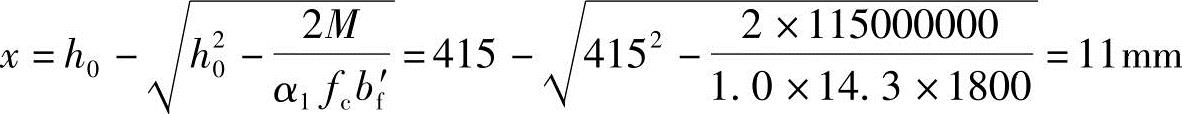
（3）验算压区高度x

由《混规》式（6.2.10-3），x=11mm<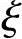_bh₀=0.518×415=214.97mm

（4）求受拉钢筋面积A_s

由《混规》式（6.2.10-2）知

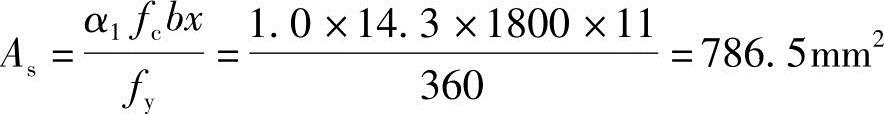
（5）验算受拉钢筋配筋率

根据《混规》第8.5.1条：

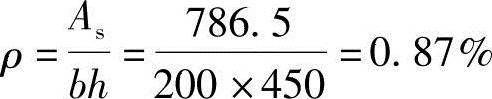
受弯纵筋最小配筋率：

ρ_min=max{0.20%，0.45f_t/f_y}=max{0.20%，0.18%}=0.2%<ρ=0.87%。满足《混规》第8.5.1条规定的构造要求。

Ⅱ.简要解答

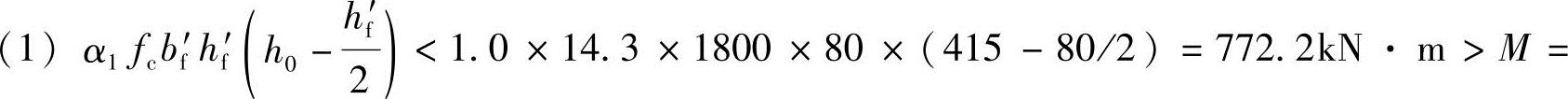
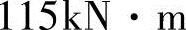，属第一类T形梁，可按截面b_f′×h=1800×450矩形截面梁计算；

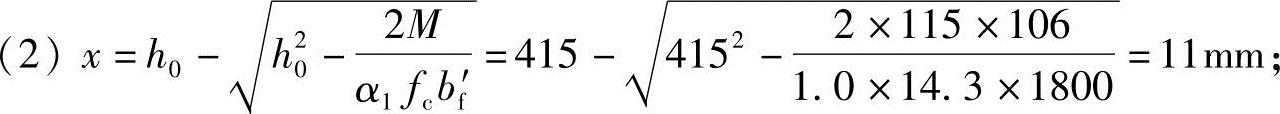
（3）x=11mm<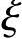_bh₀=0.518×415=14.97mm；

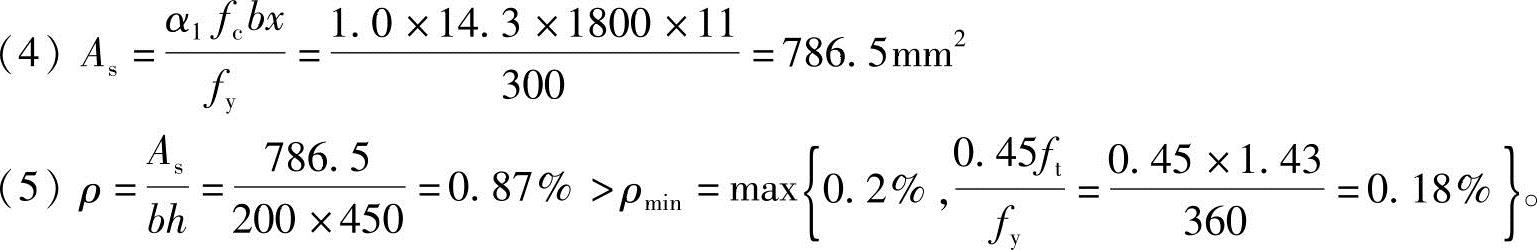
图 3.2.36

【3.2.21】 某现浇钢筋混凝土梁板结构中的次梁，截面尺寸为b×h=200mm×500mm，b_f′=800mm，h_f′=110mm，混凝土等级为C25，钢筋采用HRB400，环境类别为一类。计算简图见图3.2.36。若跨中最大弯矩设计值M_max=410kN·m，则受拉钢筋截面面积A_s（mm²）为下列何项数值？

（A）2618.0 （B）3100.2 （C）3559.9 （D）2967.1

答案：（D）

Ⅰ.详细解答

由《混规》第4.1.4条、4.2.3条、6.2.6条、6.2.7条得

f_c=11.9N/mm²，f_y=f_y′=360N/mm²，α₁=1.0，β₁=0.8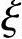，_b=0.518

因弯矩较大，截面宽度b较窄，预计受拉钢筋需排成两排，故取h₀=h-a_s=500-60=440mm

（1）判定截面类型

根据《混规》式（6.2.11-2）得

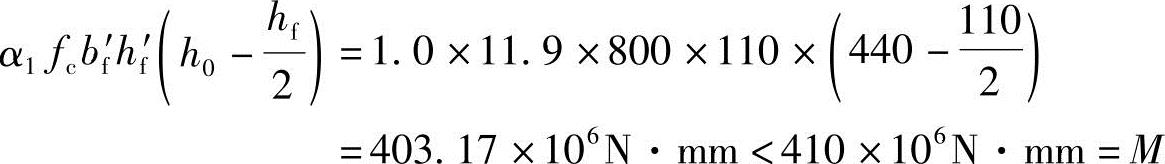
属于第二种类型的T形梁

（2）求压区高度x

由《混规》式（6.2.11-2）得

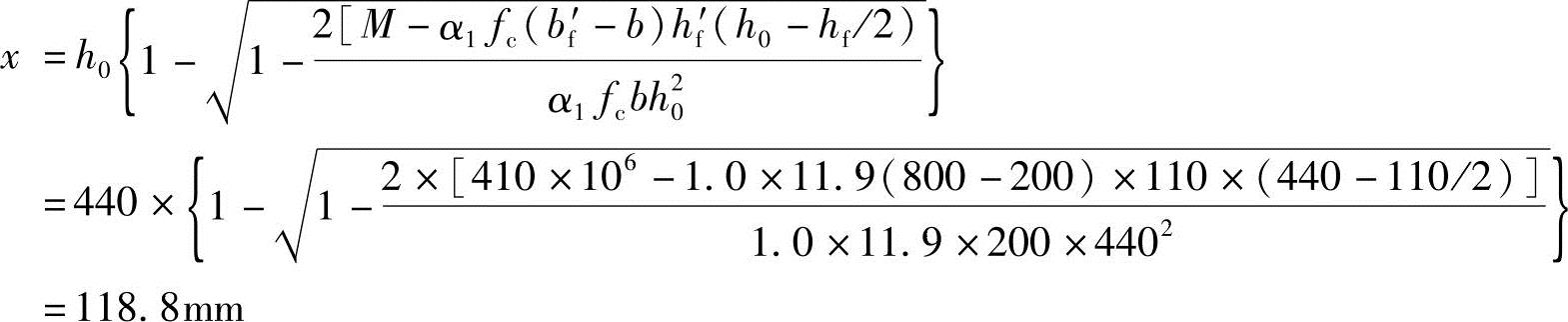
（3）验算压区高度x

由《混规》式（6.2.10-3）得

x=118.8mm<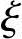_bh₀=0.518×440=227.9mm

（4）计算受拉钢筋面积A_s

由《混规》式（6.2.11-3）得

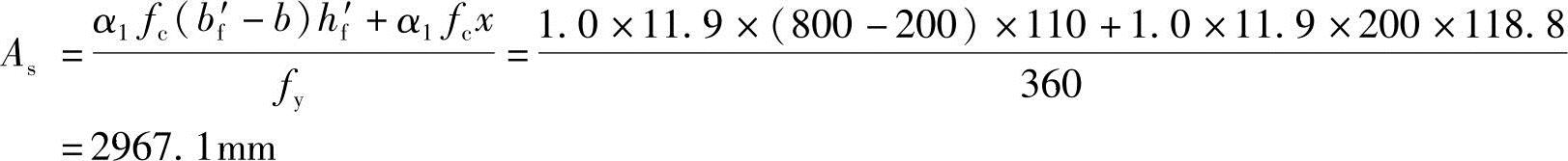
Ⅱ.简要解答

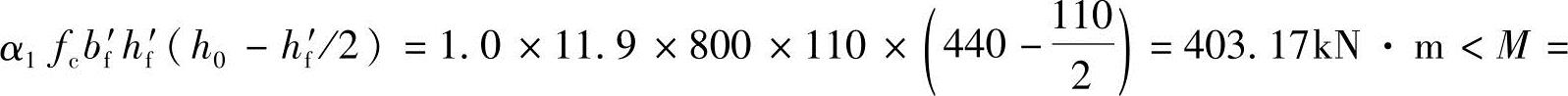
（1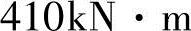），属第二类T形梁；

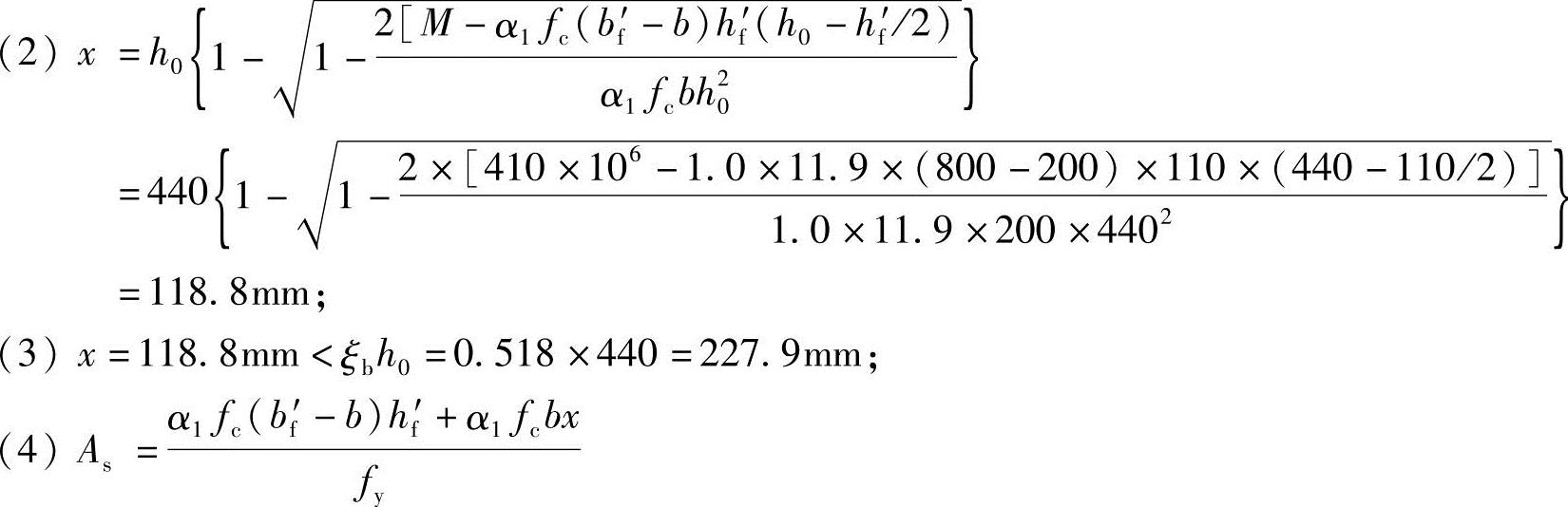
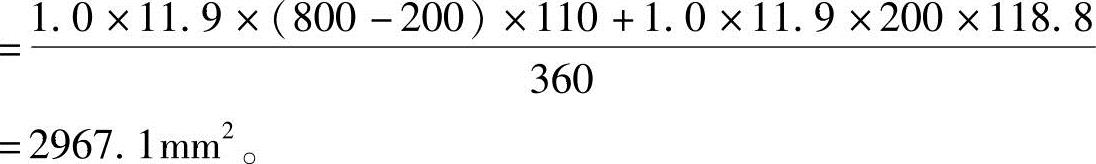
【3.2.22】 箱形梁的承载力计算（2009年，因规范改版，本题已作相应调整）。

某承受竖向作用的钢筋混凝土箱形截面梁，截面尺寸如图3.2.37所示；作用在梁上的荷载为均布荷载；混凝土强度等级为C25（f_c=11.9N/mm²，f_t=1.27N/mm²），纵向钢筋HRB400级，a_s=a_s′=40mm，已知该梁下部纵向钢筋配置为620。试问，该梁跨中正截面受弯承载力设计值M（kN·m）与下列哪个值最为接近？

提示：不考虑侧面纵向钢筋及上部受压钢筋的作用

（A）365 （B）410

（C）425 （D）480

答案：（D）

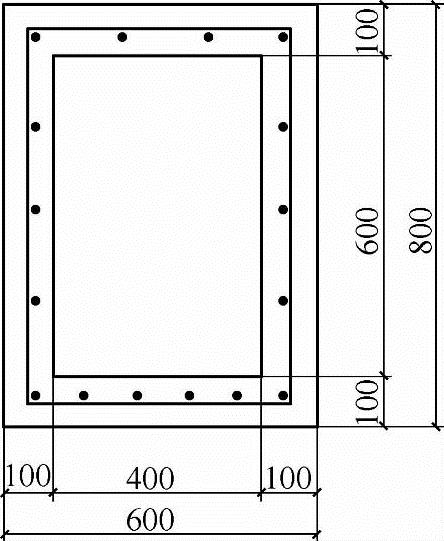
图 3.2.37

（1）A_sf_y=1884×360=678240N<α₁f_cb_f′h_f′=1.0×11.9×600×100=714000N，按宽度为b_f′的矩形截面计算；

（2）A_sf_y=α₁f_cb_f′x

678240=1.0×11.9×600·x 解得：x=95mm

【3.2.23】 双筋T形梁的承载力计算（2009，因规范改版，本题已作相应调整）。

某办公楼现浇钢筋混凝土三跨连续梁如图3.2.38a所示，其结构安全等级为二级，混凝土强度等级为C30，纵向钢筋采用HRB400级钢筋（），箍筋采用HPB300级钢筋（）。该梁AB跨跨中纵向受拉钢筋为425（A_s=1964mm²），跨中纵向受压钢筋为222（A_s′=760mm²），截面尺寸如图3.2.38b所示，b_f′=900mm，a_s=a_s′=40mm。试问，该T形梁跨中截面受弯承载力设计值M（kN·m）与以下何项数值最为接近？

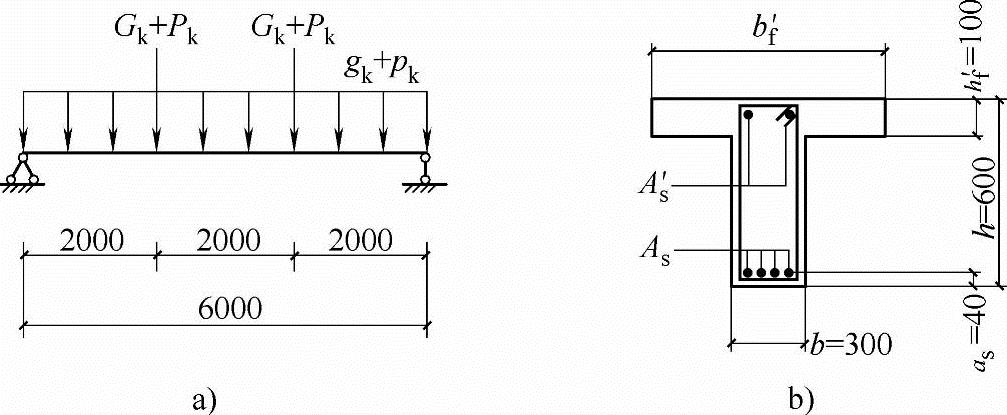
图 3.2.38

（A）289 （B）306 （C）317 （D）368

答案：（D）

（1）A_sf_y=1964×360=707040N

<A_s′f_y′+α₁f_cb_f′h_f′=760×360+1.0×14.3×900×100=1560600N

按b_f′宽的矩形截面计算。

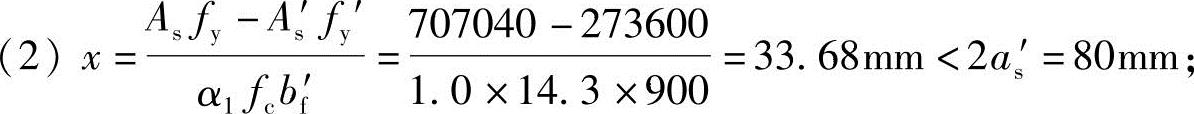
（3）按《混规》6.2.14条：

M=A_sf_y（h₀-a_s′）=1964×360×（560-40）=367.66kN·m