发动机载荷谱及其应用：时间历程和频域分析

一般载荷频域分析不作幅值谱和相位谱分析，而是用具有统计特性的功率谱密度来作谱分析，如果从功率谱密度函数上发现载荷的频率很高，则用功率谱密度函数曲线和数值作为载荷谱。

平稳随机过程的功率谱密度函数与自相关函数是傅里叶变换偶对，即

因为自相关函数是偶函数，所以功率谱密度是非负实偶函数，在实际中，用定义在非负频率上的谱更为方便，这种谱称为单边功率谱密度函数。表示为

由信号处理的相关理论可知，数字信号处理只能对有限长的信号进行分析运算，即需要对信号进行时域截断处理。相应地，这种时域截断必然造成频谱分析时出现谱峰下降、频谱扩展的现象，即引起频谱泄漏，使谱估计与真实值之间的误差加大。同时，用离散谱来近似表示连续波形的特性还将出现栅栏效应，通过加窗处理和增加序列长度可以减轻它们带来的误差。合适窗函数的加权作用是使被加权序列在边缘比矩形窗函数圆滑而减小了陡峭的边缘所引起的副瓣分量。频率泄漏的大小与数据窗的形状和长度有关，在空间域里的不同数据窗，对应到频率域也有不同的窗，频域窗函数是由时域窗函数经傅里叶变换得到的。目前，常用的几种窗函数有矩形窗、三角窗、汉宁窗、汉明窗，这四种窗函数各自具有不同的特点，它们泄漏频率的旁瓣峰值依次减小，阻带最小衰减也依次减小，但过渡带随之增加，这表示随着频率泄漏的减弱，其频带加宽，从而更容易发生频率混叠而降低分析精度。可见，减小主瓣宽度和衰减旁瓣峰值是一对矛盾，只能针对不同的要求来合理选取窗函数。对比而言，汉宁窗具有较好的综合特性，它的旁瓣小且衰减快，适合于随机信号和周期信号的截断与加窗，部分典型工况下增压器转速信号功率谱密度分别如图12－34、图12－35所示。(www.xing528.com)

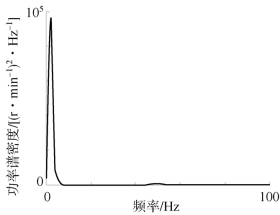
图12－34　起步过程增压器转速功率谱密度

图12－35　换挡过程增压器转速功率谱密度

观察各典型工况下增压器转速功率谱密度分布图可以发现，各段信号频率构成有所区别，但最大频率均小于60 Hz，且能量大部分集中在10 Hz以内。根据现有理论认为，在此情况下，机件的损伤与幅值的大小和出现的次数有关，因此必须作幅值分布分析。