发动机载荷谱与应用分析

废气涡轮增压是内燃机与叶轮机的结合与协同工作。涡轮叶轮将柴油机排出的废气能量转变为机械能，驱动同轴的压气机叶轮高速旋转，压缩新鲜空气经中冷后进入柴油机气缸，增加柴油机充气量，进而燃烧更多燃油，达到提高柴油机工作效率、减少油耗的目的。

对于一般的离心式压气机来说，流量与转速成正比，等熵压缩功与转速的平方成正比，因此在高转速时有大流量、高压比的特点，在低转速时有小流量、低压比的特点。在增压柴油机中，当柴油机的负荷增大时，燃油喷射量将随之增加，排气温度升高，因而供给涡轮的热能增加，使涡轮转速上升，使压气机的出口压力、温度升高。

分别以该型柴油机工作在1 500 r/min、2 000 r/min下不同负荷时的压气机后空气温度、空气压力及增压器转速的台架试验测试数据为样本，进行相关性分析，台架试验测试数据见表12－1、表12－2。

表12－1　压气机后空气温度、空气压力及增压器转速（柴油机转速为1 500 r/m in）

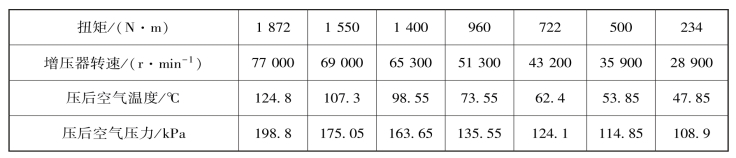
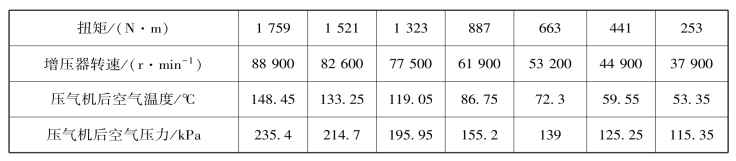
表12－2　压气机后空气温度、空气压力及增压器转速（柴油机转速为2 000 r/m in）

1.增压器转速与压气机后空气温度

压气机后空气温度与增压器转速的离散点图及平滑曲线分别如图12－3、图12－4所示。根据离散点图的变化趋势，采用多项式回归建立样本回归模型。

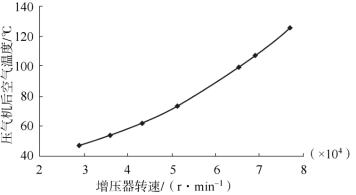
图12－3　1 500 r/m in时离散点图及平滑曲线

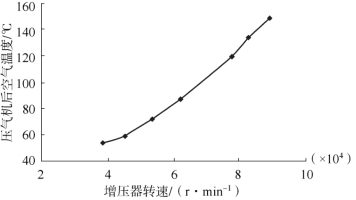
图12－4　2 000 r/m in时离散点图及平滑曲线

（1）柴油机转速为1 500 r/min时样本回归模型为

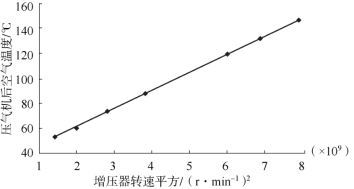
做回归方程显著性检验：F＝1 1612.7，Prob＞F的值小于0.000 1，表明当显著性水平α＝0.01时，回归方程是显著的。回归常数及回归系数t检验均有Prob＞值小于0.000 1，表明当显著性水平α＝0.01时，回归常数及回归系数是显著的。压气机后空气温度与增压器转速的平方值的离散点及回归直线如图12－5所示。

（2）柴油机转速为2 000 r/min时样本回归模型为

做回归方程显著性检验：F＝7 065，Prob＞F的值小于0.000 1，表明当显著性水平α＝0.01时，回归方程是显著的。回归常数及回归系数t检验均有Prob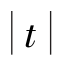＞值小于0.000 1，表明当显著性水平α＝0.01时，回归常数及回归系数是显著的。压气机后空气温度与增压器转速的平方值的离散点及回归直线如图12－6所示。

(www.xing528.com)

图12－5　1 500 r/m in时样本离散点图及回归直线

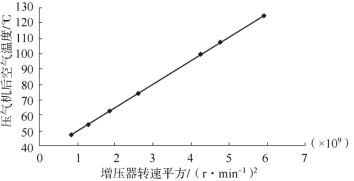
图12－6　2 000 r/m in时样本离散点图及回归直线

2.增压器转速与压气机后空气压力

压气机后空气压力与增压器转速的离散点图及平滑曲线分别如图12－7、图12－8所示。根据离散点图的变化趋势，采用多项式回归建立样本回归模型。

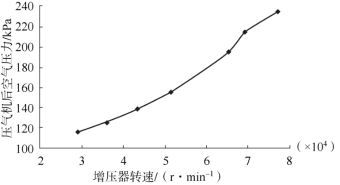
图12－7　1 500 r/m in时离散点图及平滑曲线

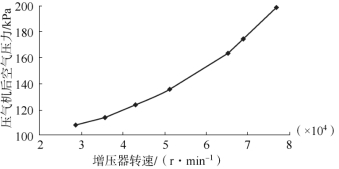
图12－8　2 000 r/m in时离散点图及平滑曲线

（1）柴油机转速为1 500 r/min时样本回归模型为

做回归方程显著性检验：F＝1 143.38，Prob＞F的值小于0.000 1，表明当显著性水平α＝0.01时，回归方程是显著的。回归常数及回归系数t检验均有Prob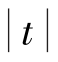＞值小于0.000 1，表明当显著性水平α＝0.01时，回归常数及回归系数是显著的。压气机后空气压力与增压器转速的平方值的离散点及回归直线如图12－9所示。

（2）柴油机转速为2 000 r/min时样本回归模型为

做回归方程显著性检验：F＝2 877.41，Prob＞F的值小于0.000 1，表明当显著性水平α＝0.01时，回归方程是显著的。回归常数及回归系数t检验均有Prob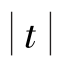＞值小于0.000 1，表明当显著性水平α＝0.01时，回归常数及回归系数是显著的，压气机后空气压力与增压器转速的平方值的离散点及回归直线如图12－10所示。

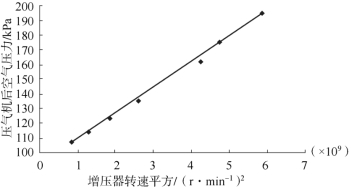
图12－9　1 500 r/m in时样本离散点图及回归直线

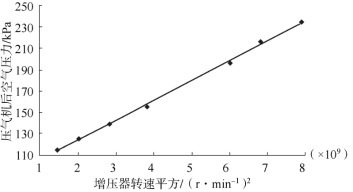
图12－10　2 000 r/m in时样本离散点图及回归直线

可见，该型柴油机在各转速下压气机后空气温度、空气压力与增压器转速平方值的回归模型的回归系数均大于零，这表明：在一定环境条件下，随着增压器转速的升高，压气机后空气温度、空气压力也跟随着增加且与增压器转速的平方成正比。因此，转速可作为表征压气机叶轮运行工况的特征参数，所以压气机载荷谱主要是转速谱（即转速－时间历程）。