随机数检验结果-车辆发动机载荷谱及其应用

伪均匀随机数的有效性在于它们与真正的[0，1]区间上均匀随机数的性质是否有显著差异，若二者有显著差异，则这种通过随机数发生器产生的随机变量样本就不能够反映该随机变量的性质，从而无法得到可靠的随机模拟结果。

1.参数检验

均匀随机数的参数检验是检验由某个发生器产生的随机数序列{ri}的均值、方差和各阶矩与均匀分布的理论值是否有显著差异。

若随机变量R～U（0，1），则若R1，R2，…，Rn是均匀总体R的简单随机样本，即R1，R2，…，Rn相互独立服从U（0，1）分布，记

则有

2.均匀性检验

随机数的均匀检验又称为频率检验，它用来检验由某个发生器产生的随机数序列{ri}是否均匀地分布在[0，1]区间，也就是检验经验频率与理论频率的差异是否显著，目前常用的方法是χ2检验。

χ2检验的理论依据是：如果从一个随机变量R中随机抽取若干观察样本，这些观察样本落在R的m个互不相交的子集中的频数服从一个多项分布，这个多项分布在m趋向于无穷时近似服从卡方分布。(www.xing528.com)

设r1，r2，…，rn是待检验的一组随机数，假设H0：r1，r2，…，rn为均匀总体的简单样本。将[0，1]区间分为m个小区间，以表示第i个小区间，设{rj}（j＝1，2，…，n）落入第i个小区间的数目为ni（i＝1，2，…，m）。根据均匀性假设，rj落入每个小区间的概率为，第i个小区间的理论频数，统计量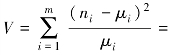渐进服从χ2（m－1）。

给定显著性水平α，查χ2分布表得临界值后，即可对经验频率与理论频率的差异作显著性检验。若χ2的概率P值小于显著性水平α，则应拒绝原假设，认为样本来自的总体分布与期望分布或某一理论分布存在显著差异；反之，则不能拒绝原假设，可以认为样本来自的总体分布与期望分布或某一理论分布不存在显著差异。

3.独立性检验

独立性检验主要检验随机数序列r1，r2，…，rn之间的统计相关性是否显著。两个随机变量的相关系数反映它们之间的线性相关程度，若两个随机变量独立，则它们的相关系数为零，故可以利用相关系数检验随机数的独立性。

设r1，r2，…，rn是待检验的一组随机数，原假设H0：相关系数ρ＝0。考虑样本的j阶自相关系数：

相关系数范围为：－1≤ρ≤1，当｜ρ｜＜0.3时，表示变量的线性相关性较弱。计算自相关系数及标准误差概率P值：若检验统计量的概率P值小于给定的显著性水平α，则应拒绝原假设，认为变量存在线性相关性；若相反，则不应拒绝原假设，认为变量间不存在线性相关性。

当n－j充分大，且ρ＝0成立时，渐进服从N（0，1）分布（j＝1，2，…，m），可以利用统计量uj进行相关性检验。