采用四面体单元对曲轴和连杆进行网格划分，四面体网格的生成方法主要为推进波前法，它首先离散待剖分域的边界。待剖分域的边界离散后是拓扑相容的三角形面片的集合，这种离散后的域边界称为前沿。从前沿开始，依次插入一个节点，并连接生成一个新的单元，更新前沿，这样前沿就可以向待剖分域的内部推进，这种插入节点、生成新单元、更新前沿的过程循环进行，当前沿为空时表明整个域剖分结束。
由于在后续的处理计算中，考虑到曲轴和连杆进行柔性化处理后要对模型进行自由模态分析，因此在建立有限元模型时，划分网格要尽可能大小均匀，同时考虑到要对危险截面（如过渡圆角处）进行强度计算，因此在曲柄销、主轴颈与曲柄臂的过渡圆角处需要对网格进行加密，所以要考虑对节点位置的优化配置。对于用四面体单元划分完成后的构件模型，应对其网格质量加以评估。
在刚柔耦合模型中，载荷的传递必须经过外接节点单元，所以在建立柔性体有限元模型时必须采用特定的自由度连接关系，应用多点约束（Multi－Point Constraints，MPC）来实现载荷的传递。MPC是用于描述多个位移自由度之间相互关系的线性方程，在有限元计算中应用很广泛，它允许计算模型在不同的自由度之间强加约束。简单来说，MPC定义的是一种节点自由度的耦合关系，即以一个节点的某几个自由度为标准值，令其他指定节点的某几个自由度与这个标准值建立某种关系。多点约束常用于表征一些特定的物理现象，如刚性连接、铰接、滑动等，也用于不相容单元间的载荷传递。
在曲轴的连杆轴颈、主轴颈和飞轮连接处建立外接节点单元，节点单元在刚－柔性体运动连接处为柔性体提供刚性支撑，其位置与曲轴各运动副的标记点位置完全一致。对曲轴进行自由网格划分并进行质量检查和网格优化，得到曲轴有限元模型如图9－16所示，共有48 210个节点、30 800个单元和11个外接点单元。
图9－16 曲轴有限元模型（书后附彩插）
在连杆的大头和小头连接处建立外接点单元，连杆的有限元模型如图9－17所示，有10 370个节点、5 898个单元和2个外接点单元。
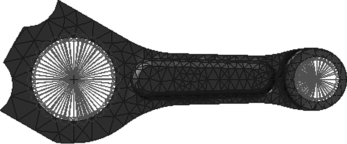
图9－17 连杆有限元模型（书后附彩插）
1.有限元模态分析
模态分析的理论过程是指以线性振动理论为基础，研究激励、系统、响应三者的关系。它是研究结构动力特性的一种近代方法，是系统辨别方法在工程振动领域中的应用。模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得，这样的一个计算或试验分析过程称为模态分析。根据振动理论及有限元理论，具有有限个自由度的弹性系统的振动微分方程为
式中，M，C，K——结构总质量矩阵、结构总阻尼矩阵、结构总刚度矩阵；
，
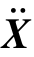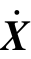，X——结构的加速度向量、速度向量和位移向量；
F（t）——结构的激振力向量。
离散为有限元三维实体单元，分别求出每个单元的刚度矩阵为
式中，D——弹性矩阵；
Bi，Bj——应力、应变关系矩阵。
曲轴的各阶自由模态振型在低阶频率下，以弯曲模态为主，并且弯曲变形的最大部位出现在主轴颈和曲柄销与曲柄臂和平衡块的结合处。随着模态频率进一步提高，出现各部分不同步的弯曲、扭转或弯扭组合振动以及复杂的局部振动。曲轴的裂纹一般是由弯曲力矩疲劳破坏产生的，因此研究曲轴的低阶模态在外加载荷作用下的动态应变，对曲轴的强度分析具有十分重要的意义。连杆的各阶自由模态振型在低阶频率下，以弯曲模态为主，随着模态频率的提高，扭转模态振型趋于明显，随着模态频率进一步提高，出现各部分不同步的弯曲、扭转或弯扭组合振动以及复杂的局部振动。(www.xing528.com)
2.模型降阶
复杂结构动力学分析经常使用自由度非常庞大的模型，其振动模态数目多且密集，导致计算效率低下，为了提高动力学计算的效率，人们提出了许多模型降阶的方法。根据实际计算经验，通常模态的贡献量随着频率的增加而减小，即结构体系中只有少数较低的模态容易被激发，而高阶模态不易被激发。因此，缩减模型规模的一个简单方法是直接对结构的模态进行截断，舍弃高阶模态，只将自振频率低的几个模态进行叠加来表达结构的振动状态。对于具体问题，模态截断阶数的选取还需结合具体的结构和动荷载，采用适当的判据进行分析判断。如果不能对各阶模态在系统响应中的贡献量进行较好的分析而任意截断高阶模态，就可能导致模态丢失，对模型造成影响。将系统各阶模态的“DC增益”作为模态截断的判断指标，对振动模态进行排序，以确定各阶模态对系统响应贡献量的大小，建立系统模态选取的判据。
3.约束边界条件施加
曲柄连杆机构的各零部件是按照一定的运动关系组合在一起的，根据零部件之间的实际运动关系将其简化成理想约束，组装成一个完整的机构。设定气缸套与地面、活塞与活塞销、曲轴和飞轮之间为固定副；活塞沿气缸中心线做直线往复运动，为移动副；活塞销与连杆、曲轴销与连杆、曲轴与地面之间为转动副。各零部件之间的运动约束关系如图9－18所示。
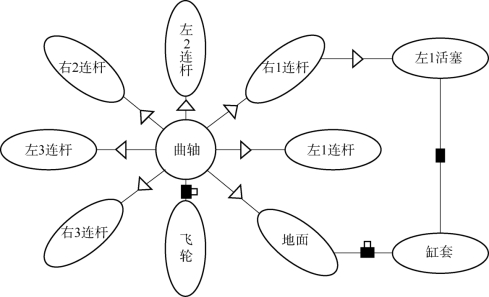
图9－18 曲柄连杆机构运动约束关系
4.载荷边界条件施加
根据发动机台架试验测得的数据，对活塞顶上作用的各缸气体爆发压力建立气体压力样条曲线。在多体动力学模型中，6个气缸都按照一定的相位关系，以曲轴转角为自变量分别调用各缸气体作用力数据文件。图9－19所示为转速为2 200 r/min时一个工作循环内各缸气体作用力曲线。
测量曲轴转角α和连杆摆角β，并以此为自变量，计算发动机的输出扭矩：
式中，PΣ——作用在活塞销中心处的合力；
R——曲轴旋转半径。
将此扭矩作为阻力矩施加在曲轴输出端，使发动机运转保持平稳。
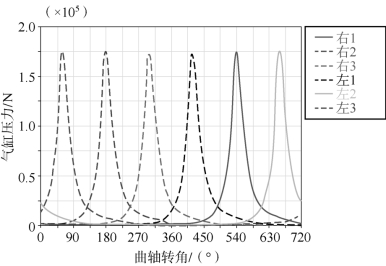
图9－19 各缸气体作用力曲线（书后附彩插）
将模态分析后得到的模态中性文件替换原刚性构件，得到包含柔性体的刚柔耦合动力学模型。调整柔性体的位置，使其重心与原刚体构件的重心对齐，这样柔性体的位置与原刚性体的位置就完全重合了。替换后，原刚体上的运动副、载荷等会自动转移到柔性体上，运动副作用中心会自动转移到柔性体距离该作用中心最近的节点上，也就是建立的外接节点。原刚体的质量、重心等固有属性均转移至柔性体上，新的柔性体将集成原来刚体的一些特征，如初始速度、模态位移等。针对研究对象的不同，将刚体动力学模型中的曲轴和连杆分别替换为柔性体，得到曲轴为柔性体和连杆为柔性体的刚柔耦合模型，如图9－20所示。
图9－20 曲柄连杆机构刚柔耦合模型（书后附彩插）
（a）曲轴为柔性体；（b）连杆为柔性体
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
