车辆发动机载荷谱与应用：多柔体系统动力学

由于刚性体在受到力的作用时不会产生变形，因此在分析构件变形、研究构件在外加载荷作用下结构内部应力的大小和分布情况时，需要把模型的关键构件当成可以产生变形的柔性体来处理。在柴油机的设计过程中，需要研究关键部件（如曲轴和连杆等）在动载荷作用下其结构内部的应力和应变，并由此校核零部件的强度和疲劳寿命，必须将这些零部件作为柔性体考虑。

柔性体上任一点的坐标值可以相对惯性坐标系进行一定范围内的移动和转动，因此需要建立一组坐标来描述柔性体上各点相对动坐标的变形，这组坐标称为弹性坐标。这样柔性体上任一点的运动就是动坐标的刚性运动与弹性变形的合成运动。柔性体上各点之间存在着相对运动，需选取浮动坐标系。选取浮动坐标系的原则是：尽量减小物体刚体运动与变形运动的耦合，以便动力学方程的建立和求解。

多柔体系统动力学方程的建立，一般采用分析力学方法。对第i个柔性体，根据第二类拉格朗日方程，有

式中，Q i——作用在第i个柔性体上的广义力；

λ——拉格朗日乘子；

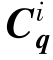——约束方程；

L——拉格朗日函数，定义为L＝T－V，T和V分别表示柔体的动能和势能；

Γ——能量耗损系数。

用式（9－23）建立多柔体动力学方程，必须求解式中的各项，柔性体的动能可表示为

代入方程：

有

式中，A，B——转换矩阵；

Φ——模态矩阵；

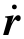——柔性体的重心矢径；

ω——柔性体的旋转角速度矢量；

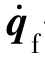——变形广义坐标；

ρ——柔性体的质量密度；

V——柔性体的体积。(www.xing528.com)

将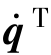和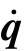提到积分号以外，可将式（9－26）写成紧缩形式：

式中，M——柔性体的质量矩阵，

柔性体的势能一般分为重力势能和弹性势能两部分，可用下列二项式来表示：

式中，Vg（q）——重力势能；

K——对应于广义坐标q的柔体广义刚度矩阵。

因为阻尼力依赖于广义速度，因此能量损耗函数Γ可表示为

式（9－30）称为Rayleigh能量损耗函数，其中阻尼矩阵D包含阻尼系数dij，为常数对称矩阵。

在多柔体系统中，各构件之间由各种铰链连接在一起，构成对多柔体系统的约束，这种约束可用约束方程来表示。在多柔体动力学分析中，形式是非线性方程组：

式中，q＝[（q1）T，（q2）T，…，（q n）T]T为系统全部广义坐标，n为广义坐标数。

经过推导，可得到多柔体系统动力学控制方程的最终形式：

式中，q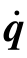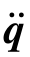，，——柔性体广义坐标及其对时间的一、二阶导数；

M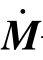，——柔性体的质量矩阵及其对时间的导数；

K——模态刚度矩阵；

fg——广义重力；

D——模态阻尼矩阵；

λ——拉格朗日乘子；

QF——外部施加的载荷。