任何弹性系统在外力(或力矩)的作用下都会产生振动。图9-12所示为单质量的弹性系统,一个有质量无弹性的圆盘3固定在一根有弹性而无质量的轴1上,轴的一端被固定。在圆盘上作用一个扭矩,使圆盘转过θ角后放开,在轴的弹性和圆盘的转动惯量作用下,圆盘恢复到原始位置并继续反方向转动θ角。如果没有阻尼,圆盘会在θ角与-θ角之间来回转动直至永远,这就是轴的扭转振动。由于没有外界干扰力矩,因此将这种扭转振动称为自由扭转振动。其偏离原始位置的最大角度即振幅,其每分钟振动的次数即自振频率(或固有频率)。当轴系加上干扰力矩时,这种振动就称为强迫扭转振动。
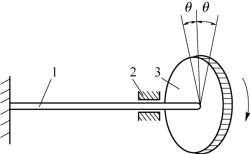
图9-12 单质量弹性系统
1—轴;2—支承;3—盘
曲轴连同与其相连的活塞组、连杆组及飞轮等构成一个多质量的弹性系统,由于对其精确计算极其困难,因此一般采用简化系统来代替。直列6缸发动机既可以简化成7质量的当量系统,也可将其再合并简化为3质量的当量系统。在将曲轴系统转换成当量系统时,应保证转换后的自振频率和振动型式与原系统相同。因此,当发动机的活塞、连杆、曲轴和飞轮的结构尺寸与材料确定后,这个弹性系统就有完全确定的自振频率,由于是多质量系统,因此具有多个自振频率。
作用于曲轴系统的干扰力矩是作用在曲柄销上的切向力引起的扭矩,这个扭矩是一个复杂的周期函数曲线,四行程发动机的周期为4π,二行程发动机的周期为3π。由受力分析可知,发动机一个气缸所发出的指示扭矩的大小为

式中,PΣ——作用在活塞销处的合力;
R——曲柄半径。
由于直接用此复杂的周期曲线来研究它对曲轴系统的干扰很困难,因此必须对它进行分解。根据傅里叶定律,可将复杂的周期函数分解成若干个简谐曲线。因此,把发动机扭矩展开为扭矩的平均值和一系列具有不同振幅、不同频率和不同初相位的简谐扭矩之和,如图9-13所示。
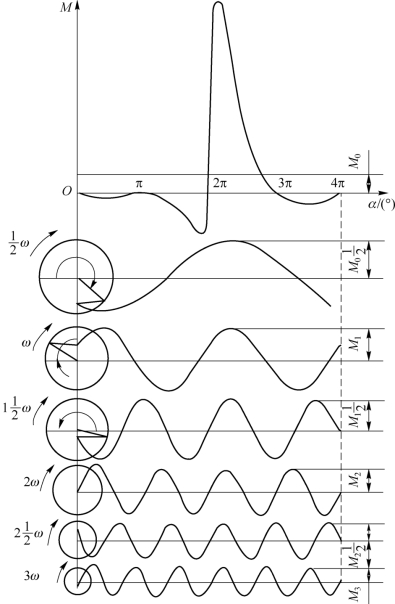
图9-13 干扰力矩的简谐分析(https://www.xing528.com)
对四行程发动机,数学表达式如下:
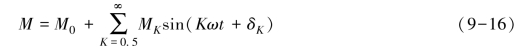
式中,M0——一个气缸的平均扭矩;
MK——K次简谐扭矩的振幅;
ω——发动机曲轴的角速度;
δK——K次简谐扭矩的初相位;
K——简谐扭矩阶数。
由于四行程发动机曲轴转两周完成一个工作循环,所以M的变化周期为4π,故K的取值为0.5,1,1.5,2,2.5,3,…
式(9-16)说明,在周期性变化的扭矩M作用下,曲轴由两种运动组成:一种是在平均扭矩M0的作用下以角速度ω的匀速旋转运动,它是对外输出扭矩;另一种是在简谐扭矩作用下所产生的不同频率(Kω)的简谐运动,它们就是扭振振动。在实际工作中,高阶的干扰力矩振幅很小,对轴系影响极小,一般情况下,将K计算到12为止,个别情况下计算到18。
发动机工作时,当简谐扭矩的频率Kω与曲轴系统中的某个自振频率相等或是它的整数倍时,曲轴系统便产生共振。产生共振时的曲轴转速就是发动机的临界转速。
产生共振时,曲轴将产生强烈的扭振振动,出现发动机的转速大幅度波动、工作不稳定、噪声大、功率下降、发动机抖动等不正常的现象。当扭转振动对曲轴所产生的附加应力超过允许限度时,曲轴有可能断裂而造成重大事故。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




