在解决实际问题中，经常需要对原始数据进行分类，以便发现规律做进一步分析。
例如，古生物研究中，通过对挖掘出的一些骨骼形状和大小将生物分类；地质勘探中，通过对矿石标本的物探、化探等指标将样本分类；市场营销学中，通过对消费者行为的研究对市场进行细分，确定目标市场；医学中，对各种病症进行分析归类；等等。聚类分析就是这样一种根据研究对象特征对研究问题进行分类的多元分析方法。
一般认为，所研究的样品（或指标）之间存在着程度不同的相似性。于是根据一批样品的多个观测指标，具体找出一些能够度量样品（或指标）之间相似程度的统计量，以这些统计量为划分类型的依据，把一些相似程度较大的样品聚为一类，关系密切的聚为一个小的分类单位，关系疏远的聚为一个大的分类单位，直到把所有样品（或指标）都聚类完毕，这样就可以形成一个由小到大的分类系统。聚类分析也有不同的分类：按聚类变量可分为样品聚类（又称Q聚类）和指标聚类（又称R聚类）；按聚类方法可分为系统聚类和动态聚类。
聚类分析是将性质相近的个体聚为一群，那如何度量“性质相近”呢？在相似性度量的选择中，常常包含许多主观上的考虑，但是最重要的考虑是指标（包括离散的、连续的和二态的）性质或观测的尺度（名义的、次序的、间隔的和比率的）。不同类型的变量，相似性的测度也不尽相同，下面介绍一些常用的度量方法。
为便于说明，设x、y是两个待测度相似性的聚类变量，它们均含有m个值。
1.数值变量的相似性测度
对样品进行聚类时，相似性一般用距离来衡量，常用的距离有以下几种定义方法。
（1）绝对值距离（city－block distance or Manhattan distances）：
（2）欧氏距离（Euclidean distances）：
（3）平方欧氏距离（squared Euclidean distances）：
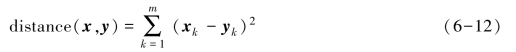
（4）切比雪夫距离（Chebychev distance）：
（5）闵可夫斯基距离（Minkowski distance）：
(www.xing528.com)
在5种距离的定义中，欧氏距离和平方欧氏距离是实际应用得最广泛的，而闵可夫斯基效力距离是5种距离中最综合的，其他距离只是它的p、r取某些特殊值时的特例而已，如表6－7所示。
表6－7 各距离间关系
（1）夹角余弦（cosine）：
（2）皮尔逊相关系数（Pearson correlation coefficient）：
有时，把1－rxy定义为距离。两个变量间的皮尔逊相关系数越大，则距离越小，说明这两个变量的性质越接近。实际上，皮尔逊相关系数就是标准化之后的夹角余弦值，由于剔除了量纲的影响，能更准确地测量变量间的关系，因此皮尔逊相关系数在实际中应用得更为广泛。
2.名义变量的相似性测度
关联测度常用于测度名义变量的相似性，一般是基于列联表来计算。设x、y均是取值为0、1的变量，两个变量间的列联表如表6－8所示。其中，a表示x、y均取0时的配对个数；b表示x取1、y取0时的配对个数；c表示x取0、y取1时的配对个数；d表示x、y均取1时的配对个数。x共有a＋c个值取0，y共有a＋b个值取0；每对变量共有a＋b＋c＋d个值。
表6－8 列联表
常用的关联测度方法是不匹配系数（percent disagreement），即x、y取值不相同的个数与取值总数之比：
还要说明的是，适用于非数值变量的测度也一定适用于数值变量，但适用于数值变量的测度基本不能用于非数值变量。不同距离的选择对于聚类的结果是有重要影响的，因此在选择相似性测度时，一定要结合变量性质。前面介绍的大部分度量方法受变量的测量单位影响较大，数量级较大的数据变异性也较大，这相当于对这个变量赋予了更大权重，从而导致聚类结果产生很大偏差。为了克服测量单位的影响，通常在计算相似测度前，要对变量进行标准化处理，将原始变量变成均值为0、方差为1的标准化变量。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
